目录

1.1 问题

福斯特问题例

1.2 数学模型

1.3 excel求解

第一步：建立一个工作表

第二步：求解器求解

---

1.1 问题

运输问题通常出现在计划货物配送机从供给地区到达需求地区之间的服务中，一般供给地区货物数量有限，需求地区货物需求量已知。常见目标是使货物从起点到终点的运输成本最低。

福斯特问题例：

       福斯特发电机公司面临一个运输问题，从3个加工厂运输一种产品到4个分销中心。3个加工厂在后3个月的计划期内的生产能力如下表所示：

起点	加工厂	3个月的生产能力（单位）
1	克利夫兰	5000
2	贝德福德	6000
3	约克	2500
		总计：13500

       公司通过波士顿、芝加哥、圣路易斯和莱克星顿的4个分销中心来分销这种发电机，每个分销中心的后3个月的需求预测如下：

终点	分销中心	3个月的需求预测（单位）
1	波士顿	6000
2	芝加哥	4000
3	圣路易斯	2000
4	莱克星顿	1500
		总计：13500

      各加工厂到分销中心的单位运输成本如下图所示：

起点	终点
	波士顿	芝加哥	圣路易斯	莱克星顿
克利夫兰	3	2	7	6
贝德福德	7	5	2	3
约克	2	5	4	5

      管理层想知道各个加工厂运输到分销中心的产品运输量应该是多少。我们可以用线性规划模型解决这类运输问题，用双下标决策变量来描述，表示从加工厂1克利夫兰到分销中心1波士顿的运输量，表示从加工厂1克利夫兰到分销中心2芝加哥的运输量，以此类推。一般情况下，m个起点和n个重点的运输问题的决策变量常被表示成以下形式：

      -------从起点i到终点j的运输量。i=1，2，3，...,m; j=1,2,3...,n

1.2 数学模型

        根据生产能力约束和目标函数建立线性规划模型，如下所示：

 

 

 

注意，最后一条决策变量的取值范围记得加上。

1.3 excel求解

     接下来介绍怎么使用excel求解简单的运输问题。

第一步：建立一个工作表

        首先输入运输成本、起终点供给量及终点节点的需求量。然后在工作表底端构建这个问题的线性规划问题。所有的线性规划问题都包含四个要素：决策变量、目标函数、左端约束条件和右端值。

       在单元格C13中输入公式=SUMPRODUCT(B5:E7,B17:F19)，用来计算解的总运输成本。单元格F17=SUM(B17:E17),F18、F19类推，计算各个起点运往各个分销商的供给总量。单元格B20=SUM(B17:B19)，C20到E20类推，计算的是运入各个分销商的货物量。

第二步：求解器求解

       选择数据>规划求解器，设置规划求解参数，如下图所示：

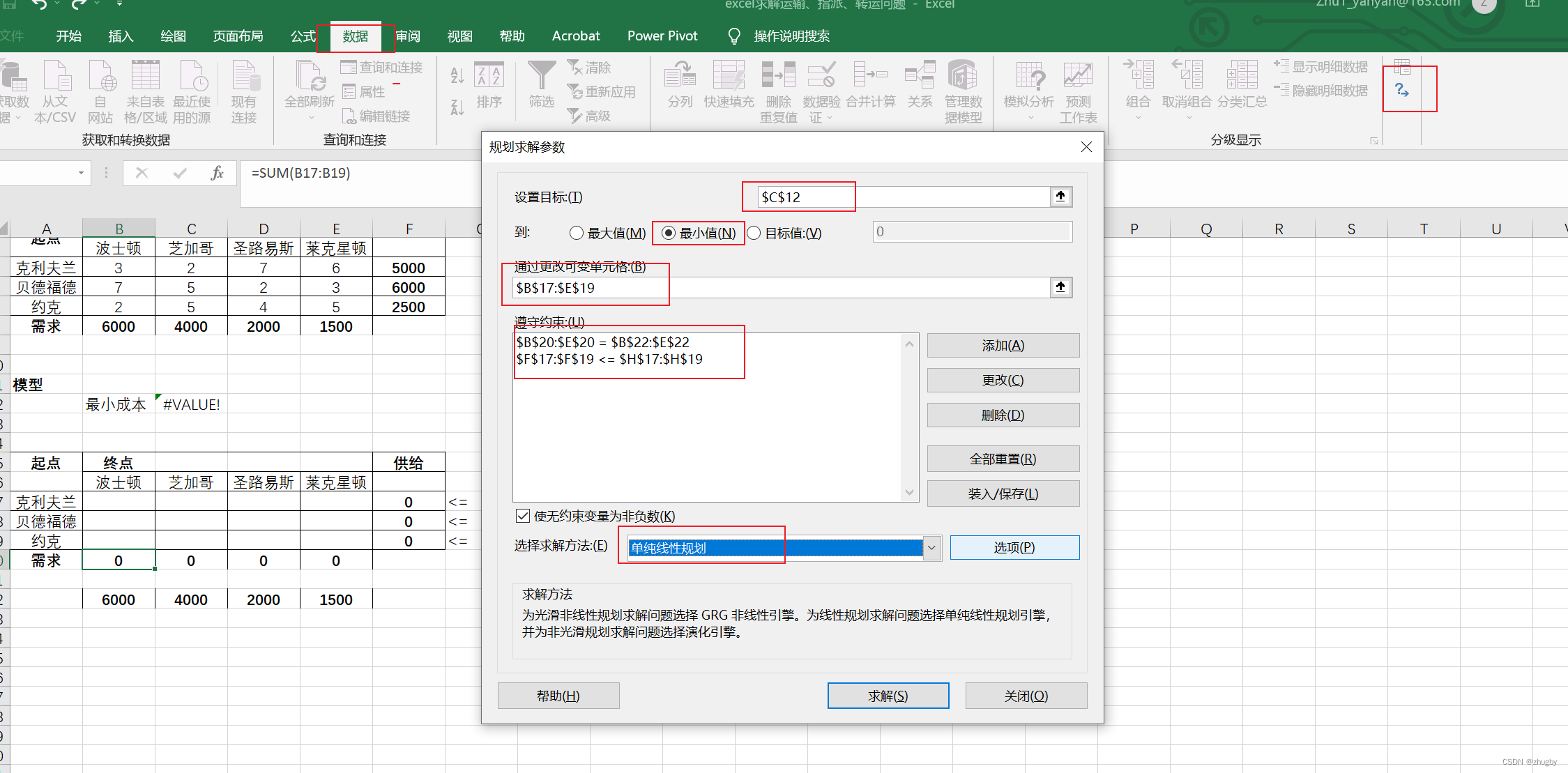
         点击求解，结果如下所示：

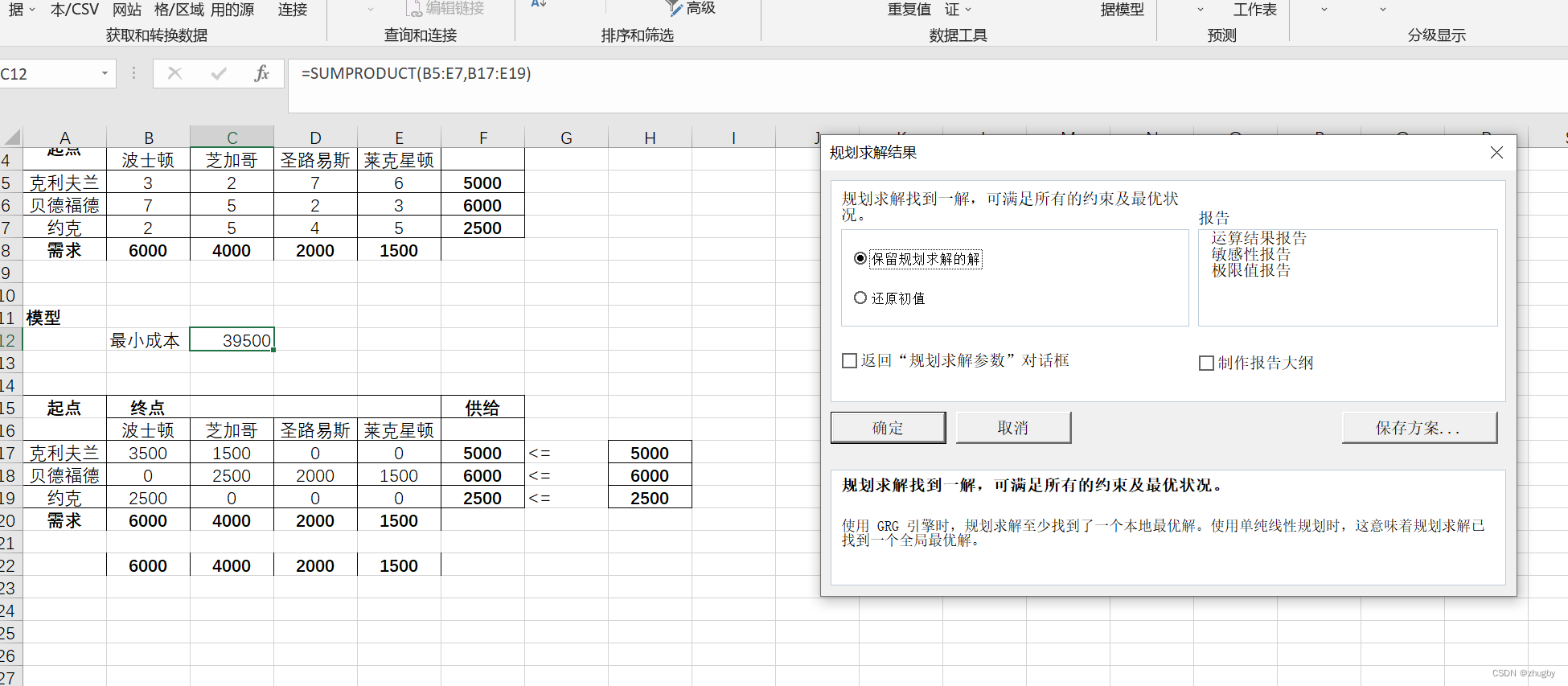
         目标函数最小值为39500，决策变量=3500，，，，，，其他决策变量都为0，即对应的路线上没有运输量。