一、定义

时间序列，是指将某种现象某一个统计指标在不同时间上的各个数值，按时间先后顺序排列而形成的序列
生活中各领域各行业有很多时间序列的数据，销售额，顾客数，访问量，股价，油价，GDP，气温。。。

二、平稳性

2.1 平稳性定义

平稳序列(stationary series)是基本上不存在趋势的序列。这类序列中的各观察值基本上在某个固定的水平上波动，虽然在不同的时间段波动的程度不同，但并不存在某种规律，其波动可以看成是随机的。

严平稳与弱平稳：

严平稳：严平稳表示的分布不随时间的改变而改变。
如：白噪声（正态），无论怎么取，都是期望为0，方差为1

白噪声序列的特点表现在任何两个时点的随机变量都不相关，序列中没有任何可以利用的动态规律，因此不能用历史数据对未来进行预测和推断。
定义：如果时间序列{εt，t=1，…，T}满足:
(1)E(εt)=0，Var(e)=σ2；
(2)对任意s≠t，εt和εs不相关，即E(εtεs)=0，
则称{εt，t=1，…，T}为白噪声序列,简称白噪声( white noise)。

宽平稳：期望与相关系数（依赖性）不变

未来某时刻的t的值Xt就要依赖于它的过去信息，所以需要依赖性

2.2平稳性的意义

预测经济系统（或其相关变量）的走势，是我们建立经济计量模型的主要目的。而基于随机变量的历史和现状来推测其未来，则是我们实施经济计量和预测的基本思路。这就需要假设随机变量的历史和现状具有代表性或可延续性。换句话说，随机变量的基本特性必须能在未来一个长时期里维持不变。否则，基于历史和现状来预测未来的思路便是错误的。

样本时间序列展现了随机变量的历史和现状，因此所谓随机变量基本性态的维持不变也就是要求样本数据时间序列的本质特征仍能延续到未来。

我们用样本时间序列的均值、方差、协（自）方差来刻画该样本时间序列的本质特征。于是，我们称这些统计量的取值在未来仍能保持不变的样本时间序列具有平稳性。可见，一个平稳的时间序列指的是：遥想未来所能获得的样本时间序列，我们能断定其均值、方差、协方差必定与眼下已获得的样本时间序列等同。也就是说，均值、方差、协方差必定为常数，不然就是不平稳的，即x和e无关，e服从标准正态分布。那么由此公式生成的时间序列就为非平稳序列。

三、单位根检验

3.1单位根定义

ADF检验全称是 Augmented Dickey-Fuller test，可以认为是一个自回归过程：
$X_t=\alpha \ast X_{t-1}+e_t$，其中$r(X,e)=0,e\sim N(0,1)$

• 如果|a|<1,则上式为平稳序列
• 如果|a|=1,就是单位根过程

当单位根存在时，自变量和因变量之间的关系具有欺骗性，因为残差序列的任何误差都不会随着样本量（即时期数）增大而衰减，也就是说模型中的残差的影响是永久的。这种回归又称作伪回归。如果单位根存在，这个过程就是一个随机漫步（random walk）。

我们用Python写个简单的函数来测试一下

def time_series(a,n):#a为系数，n为序列长度
    x = [0.0] * n #序列为n的数列
    x[0] = 0.0    #起始的数据定义为0
    for i in range(1,n):
        x[i] = a*x[i-1] + np.random.normal(0, 1, 1)#随机生成数据
    pd.DataFrame(x)[0].astype(float).plot(label = '%.2f,%d'%(a,n) ) 
    plt.legend(loc='best',fontsize = 30)
    return x       

我们先看当a<1时，

fig, ax = plt.subplots(figsize = (15,9))

plt.subplot(221)
x1=time_series(0.05,1000)

plt.subplot(222)
x1=time_series(0.5,1000)


plt.subplot(223)
x1=time_series(0.99,1000)


plt.subplot(224)
x1=time_series(0.99,10000)

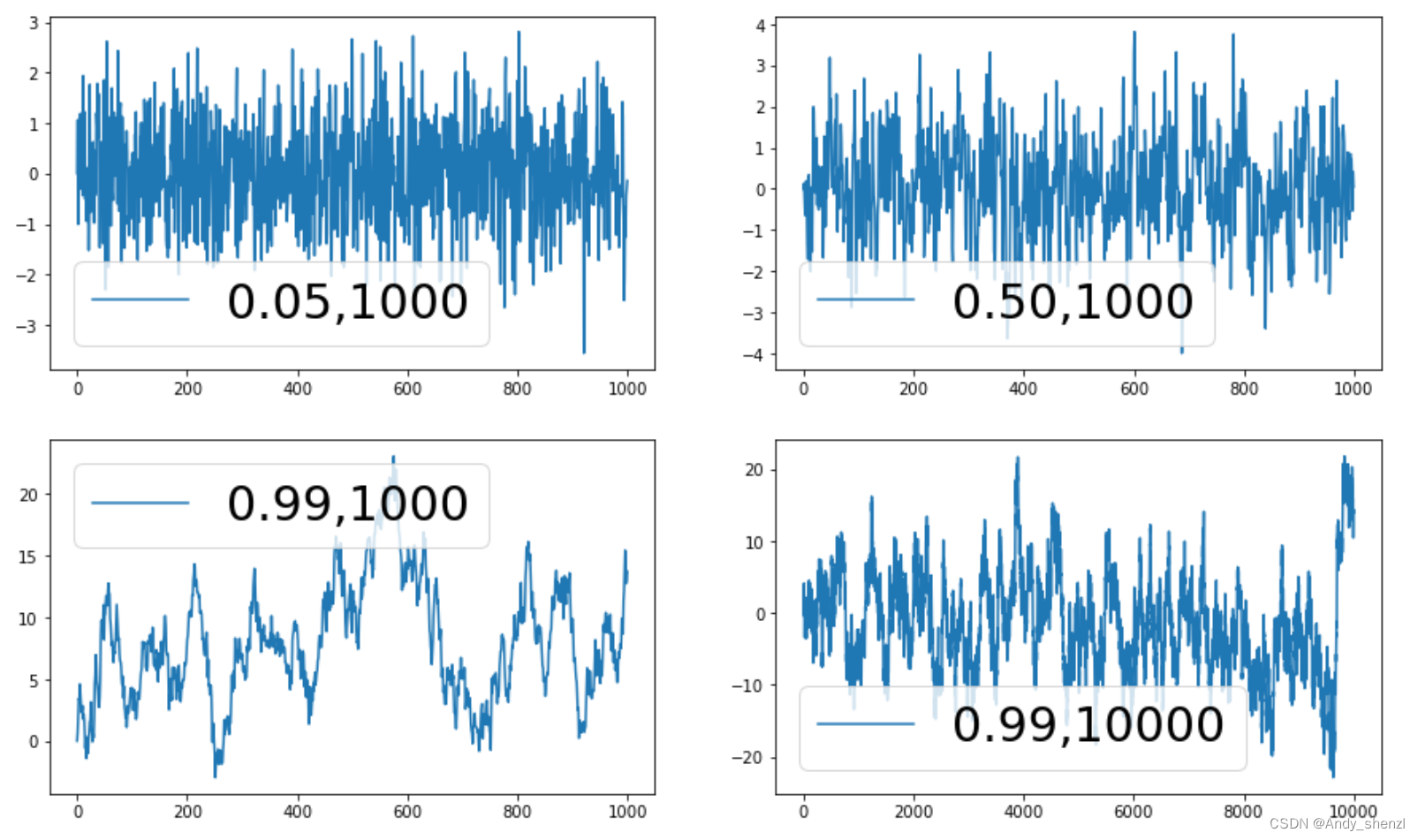
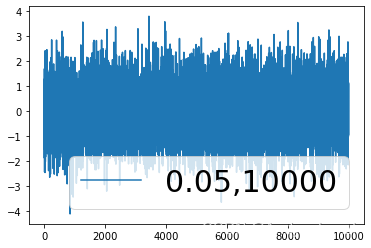
• 当a = 0.05时，我们可以发现生成的1000条数据基本上是在0为中心的附近上下波动，没有明显的趋势
• 当a = 0.5时，我们可以发现生成的1000条数据基本上是在0为中心的附近上下波动，但是上下波动的范围明显要比a = 0.05时要大一些，但没有明显的趋势
• 当a = 0.99时，我们可以发现生成的1000条数据已经开始有些上升的趋势了
• 当a = 0.99，当我们把数据加大到10000条时，我们发现数据又呈现在0为中心的附近上下波动的平稳数据了，但是上下波动的范围明显要比a = 0.05时要大很多；

结论：
在a<1时

a越大，数据的波动范围越大

a越大, 时间序列的趋势性越强，回归到均值所需的时间越久.

只要 a<1 , 时间序列依然围绕均值0上下波动，只是波动范围越大，回到均值所用时间拉长而已.

我们先看当a=1时，

fig, ax = plt.subplots(figsize = (15,9))

plt.subplot(221)
x1=time_series(1,100)

plt.subplot(222)
x1=time_series(1,1000)


plt.subplot(223)
x1=time_series(1,5000)


plt.subplot(224)
x1=time_series(1,10000)

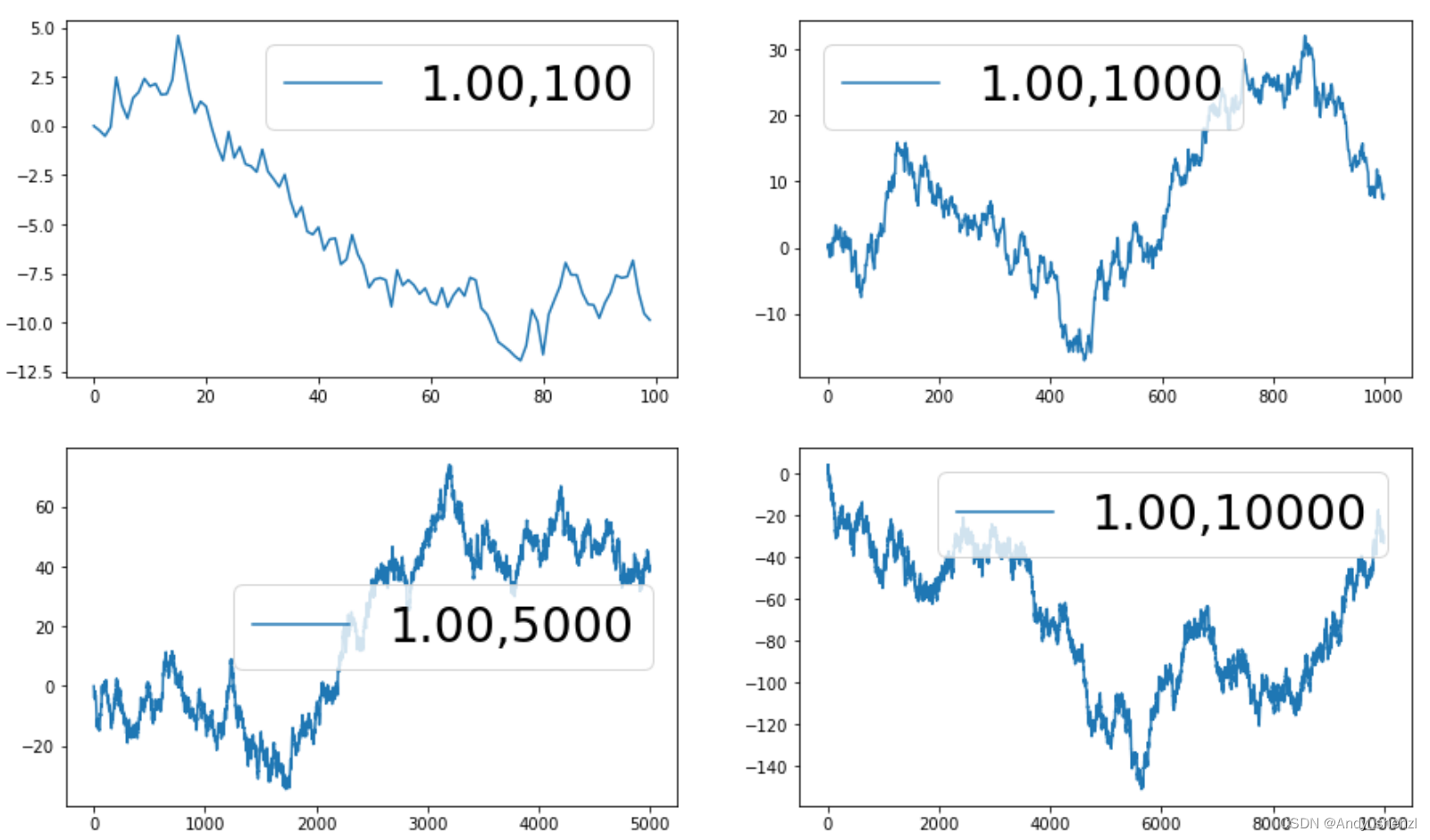
a=1时,数据会呈现明显的向上或者向下的趋势
无论时间多久，序列几乎不可能回到均值0， 这是非平稳时间序列的典型特征. 序列具有记忆性， 每次在新的起点上加入新的冲击，而历史冲击不会衰减.

序列越长，历史冲击的影响越来越小。 通过不同序列长度对比可知，正是这种历史冲击的影响差异，造成单位根过程无法回到均值附近。

结论：
记忆性越差，数据随机性越强，越能快速回到均值附近.

3.2 单位根检验

ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

ADF检验的 H0 假设就是存在单位根，如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95，99%）的把握来拒绝原假设。

我们使用statsmodels包里面的adfuller来进行检验
随机生成一组数据

x1=time_series(0.05,10000)

from statsmodels.tsa.stattools import adfuller
print(adfuller(x1))

(-69.12230006382143, 0.0, 1, 9998, {'1%': -3.431004228818807, '5%': -2.8618291302145686, '10%': -2.566923898875394}, 28018.032277372364)

第一部分是τ（tao）统计量的值。
第二部分是p_value的值。
第三部分是结果使用的延迟阶数。
第四部分是ADF回归和计算临界值所使用的观察次数。
第五部分是临界值。
第六部分是最大的信息准则的值（如果autolag 非空），也就是AIC或者BIC的值。
当我们看序列是否平稳的结果时，一般首先看第二部分的p_value值。如果p_value值比0.05小，证明有单位根，也就是说序列平稳。如果p_value比0.05大则证明非平稳。
源码里有一句note，如果p_value接近于0.05时，则要通过临界值进行判断。也就是说如果p_value接近于0.05就要通过第一部分τ（tao）统计量的值和第五部分的临界值进行对比。τ（tao）统计量的值比临界值小，就证明平稳，反之就是非平稳。我的检测结果τ（tao）统计量的值再临界值5%-10%之间。比5%的临界值大。这里的1%，5%，10%对应的是99%，95%，90%置信区间。
ADF检验只适合AR§模型。
且对方差齐性效果好，对异方差性效果不佳。异方差可用PP检验。

我们看到第二个值等于 0.0，小于0.05，所以不存在单位根，是平稳序列

我们生成的数据是a<1的，所以数据是平稳的

差分

定义：当前观察值中减去先前的观察值来执行求差。

差分是一种转换时间序列数据集的方法。它可以用来消除对时间的序列依赖性，即所谓的时间依赖性。这包括趋势和季节性等结构。

X = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
X_diff = [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

data = [i+1 for i in range(20)]
print(data)

plt.plot(data)
plt.show()

进行差分

x = pd.DataFrame(data).diff(1)
print(x.values)
pd.DataFrame(data).diff(1)[0].plot()

案例
我们生成一个a=1的序列

x1=time_series(1,10000)

from statsmodels.tsa.stattools import adfuller
print(adfuller(x1))

from statsmodels.tsa.stattools import adfuller
print(adfuller(x1))

(-0.11645535132862225, 0.947774650728789, 0, 9999, {'1%': -3.4310041633725734, '5%': -2.861829101294412, '10%': -2.566923883481157}, 28296.083771638478)

我们看到第二个值等于0.947774650728789，大于0.05，所以存在单位根，不平稳

所以接下来我们对原始数据做一阶差分

x1 =pd.DataFrame(x1).diff(1).dropna()
from statsmodels.tsa.stattools import adfuller
print(adfuller(x1))
(-99.2362102019425, 0.0, 0, 9998, {'1%': -3.431004228818807, '5%': -2.8618291302145686, '10%': -2.566923898875394}, 28290.18651394482)

我们看到第二个值等于 0.0，小于0.05，所以不存在单位根，是平稳序列

当我们的数据变成平稳序列后，就可以开始后面的预测分析了