目录
概念
基础知识
左移操作符(<<)
右移操作符(>>)
按位与(&)
按位或(|)
异或(^)
相关算法题
1.不能创建临时变量(第三个变量),实现俩个数的交换
方法1:
方法2:
写一个方法,返回参数中二进制中1的个数
方法1:
方法2:
方法3:
俩个int(32位)整数m和n的二进制表达中,有多少个位(bit)不同?
方法1
方法2
获取一个整数二进制序列中所有偶数位和奇数位,分别打印出二进制序列
概念
基础知识
首先,这里介绍的移位操作符和位操作符,针对的都整型,且针对都是整数在内存中存储的二进制位(以补码的形式存储),正数的原码,反码,补码相同,负数的反码等于负数的原码符号位不变,其它位,按位取反,负数的补码等于负数的反码+1
左移操作符(<<)
左移操作符是将整型的补码向左移动一位
计算规则:左边丢弃,右边补零
代码示例1
public class Test8 {
public static void main(String[] args) {
int a = 7;
int b = a<<1;
System.out.println(a);
System.out.println(b);
}
}
运行结果
分析:
 注意,这里a的值没有改变,只是a把左移1位的值赋给b,a本身并没有改变.
注意,这里a的值没有改变,只是a把左移1位的值赋给b,a本身并没有改变.
代码实例2
public class Test8 {
public static void main(String[] args) {
int a = -7;
int b = a<<1;
System.out.println(a);
System.out.println(b);
}
}运行结果

分析

根据上面俩个代码,我们不难发现,左移有乘2的特点
右移操作符(>>)
右移包括算数右移和逻辑右移
算数右移:整型的补码向右移动1位,右边丢弃,如果是正数,左边补零,如果是负数,左边补1
逻辑右移:整型的补码向右移动1位,右边丢弃,无论正负,左边都补0(基本不用)
代码示例1
public class Test8 {
public static void main(String[] args) {
int a = 7;
int b = a>>1;
System.out.println(a);
System.out.println(b);
}
}运行结果

分析

代码示例2
public class Test8 {
public static void main(String[] args) {
int a = -7;
int b = a>>1;
System.out.println(a);
System.out.println(b);
}
}运行结果

分析

按位与(&)
运算规则:有0为0,全1得1
代码示例
public class Test8 {
public static void main(String[] args) {
int a = 3;
int b = -5;
int c = a&b;
System.out.println(c);
}
}运行结果
分析

特点:
n&1可以得到n的二进制的最低位 ,借助右移,可以得到二进制表达的每一位
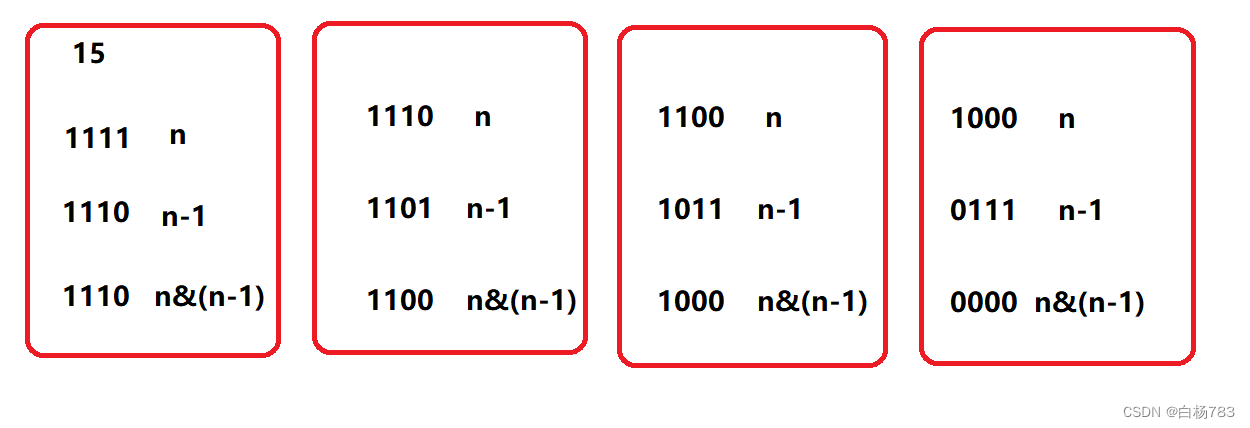
n&(n-1)可以把n的二进制位最后一个1去掉(本质是n-1借了n二进制最后的1的位,因此按位与过后,就可以把n二进制的最后的1去掉,很巧妙这个特性,也很实用),因此可以用来数二进制位1的个数,还可以判断1个数是否是2的多少次方(2的次方数的二进制都只有一个1(最高位),比如2^0 1 2^1 10 2^2 100 2^3 1000)
按位或(|)
运算规则:有1得1,全0为0
代码示例
public class Test8 {
public static void main(String[] args) {
int a = 3;
int b = -5;
int c = a|b;
System.out.println(c);
}运行结果
分析

异或(^)
运算规则:相同为0,相异为1
代码示例
public class Test8 {
public static void main(String[] args) {
int a = 3;
int b = -5;
int c = a^b;
System.out.println(c);
}
}运行结果
分析
 异或操作符的特点
异或操作符的特点
相同的俩个数异或结果位0 3^3 = 0 a^a = 0
0异或任何数,结果位这个数本身 0^2 = 2 0^a = a
异或支持交换律 2^2^5 = 5 2^5^2 = 5 a ^a^b = b,a^b^a=b
相关算法题
例题大家按顺序看哈,前面提到的公式方法,下面的题目就不提了
1.不能创建临时变量(第三个变量),实现俩个数的交换
方法1:
public class Test8 {
public static void main(String[] args) {
int a = 2;
int b = 3;
System.out.println("交换前: "+"a= "+a+" b= "+b);
a = a+b;
b = a-b;
a = a-b;
System.out.println("交换后: "+"a= "+a+" b= "+b);
}
}
我们可以巧妙的运用加减法,来做到交换a,b俩个值的目的
弊端:a+b可能数值过大越界
方法2:
public class Test8 {
public static void main(String[] args) {
int a = 2;
int b = 3;
System.out.println("交换前: "+"a= "+a+" b= "+b);
a = a^b;
b = a^b;
a = a^b;
System.out.println("交换后: "+"a= "+a+" b= "+b);
}
}
这里用到了异或交换律等特点,先不讨论上述代码,假设现在有c = a ^ b,那么如果我们拿a去异或a^b得到的就是b,拿b异或a^b得到的就是a.基于此,我们是可以通过异或来进行交换的.先拿把a^b的值赋值给a,再通过异或b得到a的值,赋值给b.最后再拿a^b异或a(此时a = a^b,b = a),得到的就是a.
写一个方法,返回参数中二进制中1的个数
方法1:
思路:对于10进制的数来说,我们可以通过%10得到10进制数的最后1位,再配合/10,我们可以依次从右向左得到10进制数的每一位,同理,对于2进制的数,我们通过%2可以得到2进制数的最后1位,再配合/2,我们可以依次从右向左得到2进制数的每一位
基于此我们可以通过%2,/2得到2进制数的每一位,再判断得到的每一位是否等于1,统计为1的个数即可

代码
public static int func(int n){
int count = 0;
int ret = n;
while(ret!=0){
if(ret%2 == 1){
count++;
}
ret = ret/2;
}
return count;
}弊端:负数的时候,此方法不可用.C语言中可以把参数设置为无符号整型 unsigned int,java俺还没想到啥改进的方法
方法2:
根据按位与的特点,我们可以知道n&1,可以得到二进制位的最低位.那么再配合右移就可以得到n二进制位的每一位.
public static int func2(int n){
int count = 0;
for (int i = 0; i < 32; i++) {
if(((n>>i)&1) == 1 ){
count++;
}
}
return count;
}弊端:循环必定会循环32次
方法3:
根据按位与的特点,n&(n-1),可以去掉n二进制表达最后的1
public static int func3(int n){
int count = 0;
while(n!=0){
n = n&(n-1);
count++;
}
return count;
}俩个int(32位)整数m和n的二进制表达中,有多少个位(bit)不同?
方法1
得到m和n二进制位的每一位,进行比较
public static int func1(int m,int n){
int count = 0;
for (int i = 0; i < 32; i++) {
if(((m>>i)&1) != ((n>>i)&1)){
count++;
}
}
return count;
}方法2
让m和n进行异或得到ret,再数ret二进制表达中有多少个1即可
public static int func2(int m,int n){
int count = 0;
int ret = m&n;
while (ret != 0){
ret = ret&(ret-1);
count++;
}
return count;
}获取一个整数二进制序列中所有偶数位和奇数位,分别打印出二进制序列
一样通过&1和右移来获取二进制表达的每一位
public static void func(int n){
//获取奇数位数字
for (int i = 30; i >=0 ; i=i-2) {
System.out.print((n>>i)&1);
}
System.out.println();
//获取偶数位数字
for (int i = 31; i >=1 ; i++) {
System.out.print((n>>i)&1);
}
}