大意：

一排电脑，每次可以选择打开一台电脑，如果某一台电脑相邻的左边和右边都被打开了，它会自动打开。问打开n台电脑的方案数

思路：

O(n^3)做法

不难发现，在操作过程中，一台台电脑其实就是被分成了几个连通块。特别的，当两个联通块的距离<=1时，它们会合并.

那么不妨首先来考虑一下如何全手动实现一个长为k的连通块的构造。显然，想要全手动连着打开k台电脑，如果我们从第i台开始的话，i后面的若干台被打开的顺序必须是固定的。如果后面有一台是跳着打开的，那么最后一定会有一台电脑被自动开启。先从考虑从第一台电脑开始打开，没什么好说的，方案数就是1，理由如上。如果从第二台电脑开始打开的话，后面几台打开的顺序固定，但是第一台可以在中间任意时间打开而不会影响最终结果，所以方案数应该为k-1。如何计算？可以采用隔板法得到。同理，从第三台电脑开始的时候，前面两台可以插入后面的任意位置，但是前面两台插入的顺序只有一种方案，所以在后面插入的时候不用考虑插入顺序，所以只需要找到位置即可，所以仍然可以采用隔板法。

最后，我们不难得到连续手动打开长度为k的连通块的方案数为

接下来考虑dp.dp[i][j]表示处理到第i位，且前面有j台电脑是手动开的。如果我们再假设最后连续k台都是手动开的，那么显然，第i-k台就是自动开的，那么第i-k-1台就是手动开的了，显然这样就可以实现从dp[i-k-1][j-k]转移到dp[i][j]了，这就是该状态设计的合理性。

具体如何转移？最后面k个手动打开的顺序方案自然就是2^(k-1)，但是它们其实也可以插入到前面打开的过程中，所以转移方程为dp[i][j]+=dp[i-k-1][j-1]*C(j,k)*2^(k-1)

最后的总方案数自然就是

O(n^2)做法

还是从联通块来入手。

我们仔细考虑一下每一次操作造成的影响。当前打开一台电脑，可能导致新产生一个连通块，也可能导致某一个联通块的电脑数量+1，当然也可能会导致两个联通块的合并。

影响的可能性就这么多，而我们最终的目标其实就是构造一个长为n的连通块。

设dp[i][j]表示i台电脑已经打开(这里跟上面设的并不一样，首先i台电脑不一定都在最前面，其次它们不一定都是手动开的)产生j个连通块的话，我们要求的就是dp[n][1]了。

然后思路就有些玄学了

先把我看到的讲一下：

---

某一个连通块长度增加：

这里有两种情况：

长度+1:也就是在连通块的左/右紧贴着添加,这样有两种选法，加上有j个块，共j*2种选法，这里：dp[i][j]+=dp[i-1][j]*j*2

长度+2：也就是隔一格开电脑，中间自动开。一样有j*2种选法，这里dp[i][j]+=dp[i-2][j]*j*2

新添加一个连通块：

上一步有j-1个连通块，所以总共有j个间隔可以插入，找一个间隔插进去就可以产生一个新的连通块了：dp[i][j]+=dp[i-1][j-1]*j

合并两个连通块：

可以发现，合并两个块也有两种情况。

第一种是两个块中间空了两个格子，随便加上一个另一个也有了。

dp[i][j]+=dp[i-2][j+1]*2*j

第二种是两个块中间空了三个格子，那么放中间就可以了

dp[i][j]+=dp[i-3][j+1]*j

---

看完上面之后，我其实是存疑的。为什么第一种情况可以认定每一个连通块都有左右两个位置可以放？为什么该情况下插入一格不会导致两个连通块的合并？因为如果两个连通块之间间隔为2的话，放入一个会导致合并，但第一种情况并没有与第三种情况进行去重。以及第二种情况，为什么随便找一个空插进去不会导致连通块合并而一定导致产生新的连通块？

这里给出我自己的解释：我之所以会产生这样的疑问，是因为我默认这n台电脑的位置是固定的，它们就摆在那里了，第一台就是第一台，它左边一定没有别的电脑了。这很合理。但是该方法其实是假设有无数台电脑。注意我们最终的目标是构造一个长为n的连通块，所以只要最终结果一样，两者的情况就是等价的。但是假设电脑有无数台的话，第一台左边就还能插新电脑。这样的好处是简化了问题，所有电脑都是等价的了，我们不用分类讨论。对于另一个疑问，我们假设我们可以自由控制两个连通块之间的距离，当我们需要通过添加一个电脑将它们连接起来时，它们的距离就是1.更加形象的，我们将连通块的连接用绳子来实现。想要一步连接两个连通块，我就将新开的电脑和两个连通块分别用绳子连接起来，就联通了。

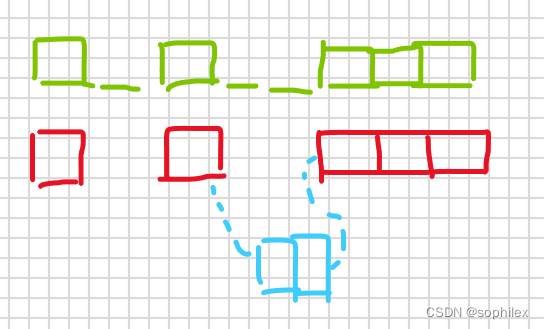
上一种是有固定距离的思路，中间插入一个就会导致连通块合并。

下一种中，由于我们用绳子，中间完全可以放好几个。不连起来的话，中间蓝色就是一个独立的连通块，连起来的话，就是一个长为5的连通块。

 这样我们就没有上述疑问了，因为连通块是否连接不再由它们的固定距离来决定，而是由我们的“绳子”来决定，这已经是一种纯粹的“构造”方案了，但是最终结果依然是产生长为n的连通块，所以合理。这是和上一种做法完全不同的思路。

所以你也可能会发现该方法的中间方案数并不对，这也是因为该方法与实际情况的思考角度不同。

code1

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=410;
//const ll mod=1e9+7;
ll n,mod;
ll ksm(ll x,ll y,ll z)
{
	ll ans=1;
	while(y)
	{
		if(y&1) ans=ans*x%z;
		x=x*x%z;
		y>>=1;
	}
	return ans;
}
ll inv(ll x,ll m)
{
	return ksm(x,m-2,m);
}
ll p[N];
ll pp[N];
void init()
{
	p[0]=1;
	for(int i=1;i<=400;++i) p[i]=p[i-1]*i%mod;
	pp[400]=inv(p[400],mod);
	for(int i=400-1;i>=0;--i) pp[i]=pp[i+1]*(i+1)%mod;
}
ll C(ll n,ll m)
{
	if(n<m) return 0;
	return p[n]*pp[m]%mod*pp[n-m]%mod;
}
ll dp[N][N];
void solve()
{
	
	cin>>n>>mod;
	init();
	for(int i=1;i<=n;++i) dp[i][i]=ksm(2,i-1,mod);
	for(int i=2;i<=n;++i)
	{
		for(int j=2;j<i;++j)
		{
			for(int k=1;k<=j;++k)
			{
				(dp[i][j]+=dp[i-k-1][j-k]*C(j,k)%mod*ksm(2,k-1,mod))%=mod;
			}
		}
	}
	ll ans=0;
	for(int i=1;i<=n;++i) (ans+=dp[n][i])%=mod;
	cout<<ans<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	//ll t;cin>>t;while(t--)
	solve();
	return 0;
}

code2

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=410;
//const ll mod=1e9+7;
ll n,mod;
ll dp[N][N];
void add(ll &a,ll b)
{
	a=(a%mod+b%mod)%mod;
}
ll mul(ll a,ll b)
{
	return a%mod*(b%mod)%mod;
}
void solve()
{
	cin>>n>>mod;
	dp[1][1]=1;
	for(int i=2;i<=n;++i)
	{
		for(int j=1;j<=n;++j)
		{
			add(dp[i][j],mul(dp[i-1][j-1],j));
			add(dp[i][j],mul(dp[i-1][j],mul(j,2)));
			add(dp[i][j],mul(dp[i-2][j],mul(j,2)));
			if(i>2) add(dp[i][j],mul(dp[i-2][j+1],mul(2,j)));
			if(i>3) add(dp[i][j],mul(dp[i-3][j+1],j));
		}
	}
	cout<<dp[n][1]<<endl;
}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	//ll t;cin>>t;while(t--)
	solve();
	return 0;
}

个人观点，如有错误欢迎指出。