$\textcolor{Green}{前言：}$

💞本专栏用于本人刷算法的过程。主要包含刷题中的感受以及知识点缺陷。对于学习者来说可以作为参考。
目前更新的算法内容会比较多，很多都是通过刷题来进行知识点的总结，其中部分来源于网络总结，如有侵权请联系。💞

文章存在时候，会随着博主的学习过程进行不间断更新，只增不减，请放心使用

目前作者正在刷题，如果想一起交流的可以添加联系方式互相学习~~欢迎大家

动态规划

一、算法介绍
- 原理
- 适用的情况
- 做题步骤：
二、算法实例
- 1. 最小花费爬楼梯
- 2. 把数字翻译成字符串
- 3. 最长公共子序列(二)
- 4. 最长公共子串
- 5. 矩阵的最小路径和

一、算法介绍

原理

思想：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法。按顺序求解子阶段，前面子问题的解为后面子问题的求解提供信息。

如果某一问题有很多重叠子问题，使用动态规划是最有效的。

动态规划中每一个状态一定是由上一个状态推导出来。

动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。

适用的情况

最优化原理：如果问题的最优解所包含的子问题的解也是最优的，称该问题具有最优子结构，即满足最优化原理。
没有后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说：某状态以后的过程不会影响以前的状态，只与当前状态有关。
有重叠子问题：子问题之间是不独立的，一个子问题在下一个近阶段可能被多次遇到。（这条性质不是动态规划适用的必要条件，但是具备这条性质那么动态规划相对于其他算法就具备一定的优势）。

做题步骤：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

二、算法实例

1. 最小花费爬楼梯

题目来源：牛客网
$\textcolor{OrangeRed}{等级：简单}$
涉及方法：动态规划

这道题是非常经典的题目，出题肯定不是这么简单的出

👉题目描述

给定一个整数数组 $cos t$ ，其中 $cos t [i]$ 是从楼梯第 $i$ 个台阶向上爬需要支付的费用，下标从 $0$ 开始。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 $0$ 或下标为 $1$ 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

数据范围：数组长度满足 $\le n \le 10^5$ ，数组中的值满足 $\le cost_i \le 10^4$

示例1

输入：[2,5,20]
返回值：5
说明：你将从下标为1的台阶开始，支付5 ，向上爬两个台阶，到达楼梯顶部。总花费为5

示例2

输入：[1,100,1,1,1,90,1,1,80,1]
返回值：6
说明：
你将从下标为 0 的台阶开始。
1.支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
2.支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
3.支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
4.支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
5.支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
6.支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

👉代码编写

👉👉方法1

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param cost int整型一维数组 
     * @return int整型
     */
    public int minCostClimbingStairs (int[] cost) {
        // write code here
        if (cost.length == 1) return cost[0];
        int dp0 = cost[0], dp1 = cost[1];
        for (int i = 2; i < cost.length; ++i) {
            int tmp = dp1;
            dp1 = Math.min(cost[i] + dp0, cost[i] + dp1);
            dp0 = tmp;
        }
        return dp0 > dp1 ? dp1 : dp0;
    }
}

👉👉方法2

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param cost int整型一维数组 
     * @return int整型
     */
    public int minCostClimbingStairs (int[] cost) {
        // write code here
        int dp[] = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; ++i) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        return Math.min(dp[dp.length - 1], dp[dp.length - 2]);
    }
}

👉 注意点

👉 可以提炼的知识

2. 把数字翻译成字符串

题目来源：牛客网
$\textcolor{OrangeRed}{等级：中等 Medium}$
涉及方法：动态规划

👉题目描述

有一种将字母编码成数字的方式： $^{'} a^{'} - > 1,^{'} b - > 2^{'}, ...,^{'} z - > 2 6^{'}$ 。

现在给一串数字，返回有多少种可能的译码结果

数据范围：字符串长度满足 $\le 90$
进阶：空间复杂度 $O (n)$ ，时间复杂度 $O (n)$

示例1

输入："12"
返回值：2
说明：2种可能的译码结果（”ab” 或”l”）

示例2

输入："31717126241541717"
返回值：192
说明：192种可能的译码结果

👉代码编写

（该思路来源于官方）

对于普通数组1-9，译码方式只有一种，但是对于11-19，21-26，译码方式有可选择的两种方案，因此我们使用动态规划将两种方案累计。
具体方法：
step 1：用辅助数组dp表示前i个数的译码方法有多少种。
step 2：对于一个数，我们可以直接译码它，也可以将其与前面的1或者2组合起来译码：如果直接译码，则dp[i]=dp[i−1]；如果组合译码，则dp[i]=dp[i−2]。
step 3：对于只有一种译码方式的，选上种dp[i−1]即可，对于满足两种译码方式（10，20不能）则是dp[i−1]+dp[i−2]
step 4：依次相加，最后的dp[length]即为所求答案。

👉👉方法1

import java.util.*;


public class Solution {
    /**
     * 解码
     * @param nums string字符串 数字串
     * @return int整型
     */
    public int solve (String nums) {
        // write code here
        if (nums.length() == 1 && nums.charAt(nums.length() - 1) == '0'){
            return 0;
        }
        if (nums.length() == 1){
            return nums.length();
        }
        if (nums.charAt(nums.length() - 1) == '0' && 
           nums.charAt(nums.length() - 2) != '1' && nums.charAt(nums.length() - 2) != '2') {
            return 0;
        }
        int dp[] = new int[nums.length() + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= nums.length(); ++i) {
            if ((nums.charAt(i - 2) == '1' && nums.charAt(i - 1) <= '9' && nums.charAt(i - 1) > '0')
                || (nums.charAt(i - 2) == '2' && nums.charAt(i - 1) <= '6' && nums.charAt(i - 1) > '0')) {
                    dp[i] = dp[i - 1] + dp[i - 2];
            } else {
                dp[i] = dp[i - 1];
            }
        }
        return dp[nums.length()];
    }
}

👉 注意点

👉 可以提炼的知识

3. 最长公共子序列(二)

题目来源：牛客网
$\textcolor{OrangeRed}{等级：Medium}$
涉及方法：动态规划

👉题目描述

给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列

数据范围： $\le |str1|,|str2| \le 2000$
要求：空间复杂度 $O(n^2)$ ，时间复杂度 $O(n^2)$

示例1

输入："1A2C3D4B56","B1D23A456A"
返回值："123456"

示例2

输入："abc","def"
返回值："-1"

示例3

输入："abc","abc"
返回值："abc"

示例4

输入："ab",""
返回值："-1"

👉代码编写

👉 注意点

子序列不是子串，子串要求所有字符必须连续，子序列不要求连续，只要求相对位置不变
注意下列方法，该方法的重点其一是求出最长公共子序列的长度，其二是求出子序列。
字符串反转reverse()，一般我们直接调用即可。这里我们使用的是(StringBuilder)sb.reverse

👉👉方法1

import java.util.*;


public class Solution {
    /**
     * longest common subsequence
     * @param s1 string字符串 the string
     * @param s2 string字符串 the string
     * @return string字符串
     */
    public String LCS (String s1, String s2) {
        // write code here
        if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
            return "-1";
        }

        // 先求最长公共子序列的长度
        int[][] dp = new int[s1.length() + 1][s2.length() + 1];
        for (int i = 1; i <= s1.length(); ++i) {
            char ch1 = s1.charAt(i - 1);
            for (int j = 1; j <= s2.length(); ++j) {
                char ch2 = s2.charAt(j - 1);
                if (ch1 == ch2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        // 求长度结束

        // 求子序列
        int row = s1.length() + 1, col = s2.length() + 1;
        if (dp[row - 1][col - 1] == 0) {
            return "-1";
        }
        StringBuilder sb = new StringBuilder();
        for (int r = row - 1, c = col - 1; dp[r][c] >= 1;) {
            if (s1.charAt(r - 1) == s2.charAt(c - 1)) {
                sb.append(s1.charAt(r - 1));
                --r;
                --c;
            } else if (dp[r - 1][c] >= dp[r][c - 1]) {
                --r;
            } else {
                --c;
            }
        }
        return sb.reverse().toString();
    }
}

👉 可以提炼的知识

4. 最长公共子串

题目来源：
$\textcolor{OrangeRed}{等级：}$
涉及方法：

👉题目描述

给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一。

数据范围： $\le |str1|,|str2| \le 5000$
要求： $空间复杂度 O(n^2)$ ，时间复杂度 $O(n^2)$

示例1

输入："1AB2345CD","12345EF"
返回值："2345"

备注： $\leq |str_1|, |str_2| \leq 5\,000$

👉代码编写

👉👉方法1

import java.util.*;


public class Solution {
    /**
     * longest common substring
     * @param str1 string字符串 the string
     * @param str2 string字符串 the string
     * @return string字符串
     */
    public String LCS (String str1, String str2) {
        // write code here
        int row = str1.length() + 1, col = str2.length() + 1;
        int[][] dp = new int[row][col];
        int max = 0, index = 0;
        for (int i = 1; i < row; ++i) {
            for (int j = 1; j < col; ++j) {
                if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    if (max < dp[i][j]) {
                        max = dp[i][j];
                        index = i;
                    }
                }
            }
        }
        return max == 0 ? "-1" : str1.substring(index - max, index);
    }
}

👉 注意点

👉 可以提炼的知识

substring()：截取字符串的一部分字符

函数用法

substring(int beginIndex)：返回从起始位置到字符串末尾
substring(int beginIndex, int endIndex)：返回从起始位置到目标位置之间的字符串，但不包含目标位置。

5. 矩阵的最小路径和

题目来源：牛客网
$\textcolor{OrangeRed}{等级：Medium}$
涉及方法：动态规划

👉题目描述

给定一个 $n * m$ 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

数据范围: $\le n,m\le 500$ ，矩阵中任意值都满足 $\le a_{i,j} \le 100$
要求：时间复杂度 $O (nm)$

例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，
所选择的最小累加和路径如下图所示：

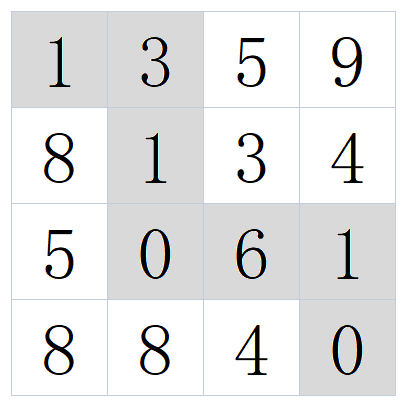
示例1

输入：[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]
返回值：12

示例2

输入：[[1,2,3],[1,2,3]]
返回值：7

备注：
$\leq n,m \leq 2000$
$\leq a_{i,j} \leq 100$

👉代码编写

👉 注意点

这个题目也比较经典，注意dp数组。同时也要看图，图是很好理解的。

👉👉方法1

import java.util.*;


public class Solution {
    /**
     * 
     * @param matrix int整型二维数组 the matrix
     * @return int整型
     */
    public int minPathSum (int[][] matrix) {
        // write code here
        int row = matrix.length, col = matrix[0].length;
        int dp[][] = new int[row][col];
        dp[0][0] = matrix[0][0];
        for (int i = 1; i < col; ++i) {
            dp[0][i] = dp[0][i - 1] + matrix[0][i];
        }
        for (int i = 1; i < row; ++i) {
            dp[i][0] = dp[i - 1][0] + matrix[i][0];
        }
        for (int i = 1; i < row; ++i) {
            for (int j = 1; j < col; ++j) {
                dp[i][j] = matrix[i][j] + Math.min(dp[i -1][j], dp[i][j - 1]);
            }
        }
        return dp[row - 1][col - 1];
    }
}