导波光学理论基础
一、电磁场基本方程
1.1 麦克斯韦方程组、物质方程、边值关系
麦克斯韦方程组

麦克斯韦方程组是一组微分方程,只能求得通解
如果需要唯一的确定各场矢量,还需补充一些边界条件
线性、静止、各向同性介质的物质方程
D ⃗ = ε E ⃗ B ⃗ = μ H ⃗ J ⃗ = σ E ⃗ \begin{aligned} \vec D&=\varepsilon \vec E \\ \vec B&=\mu\vec H \\ \vec J&=\sigma\vec E \\ \end{aligned} DBJ=εE=μH=σE
静态场、变化很慢的场的边值关系
对于2个介质分界面上的点(微分方程需要函数连续),麦克斯韦方程组的微分形式不再适用。因此通过积分形式求解界面上的边值关系,当场为静态场或变化很慢的场时,可以得到:
- n ^ ⋅ ( D 2 − D 1 ) = σ \hat{n}\cdot(D_2-D_1)=\sigma n^⋅(D2−D1)=σ ( σ \sigma σ 为界面上的面电荷密度; n ^ \hat n n^ 为界面法线方向的单位矢量)(若 σ = 0 \sigma=0 σ=0 则 D 2 n = D 1 n D_{2n}=D_{1n} D2n=D1n)
- n ^ ⋅ ( B 2 − B 1 ) = 0 \hat{n}\cdot(B_2-B_1)=0 n^⋅(B2−B1)=0 (即 B 2 n = B 1 n B_{2n}=B_{1n} B2n=B1n)
- n ^ × ( E 2 − E 1 ) = 0 \hat{n}\times(E_2-E_1)=0 n^×(E2−E1)=0 (即 E 2 t = E 1 t E_{2t}=E_{1t} E2t=E1t)
- n ^ × ( H 2 − H 1 ) = α ⃗ \hat{n}\times(H_2-H_1)=\vec\alpha n^×(H2−H1)=α ( α ⃗ \vec\alpha α 为界面处的面电流密度)(若 α ⃗ = 0 \vec\alpha=0 α=0 则 H 2 t = H 1 t H_{2t}=H_{1t} H2t=H1t)
1.2 亥姆霍兹方程
亥姆霍兹方程反应 E ⃗ \vec E E、 H ⃗ \vec H H 随空间变化的关系
考虑以下条件:
- 单色光:
E ⃗ ( r ⃗ , t ) = E ⃗ ( r ⃗ ) e − j ω t H ⃗ ( r ⃗ , t ) = H ⃗ ( r ⃗ ) e − j ω t \vec E(\vec r,t)=\vec E(\vec r)e^{-j\omega t} \\ \vec H(\vec r,t)=\vec H(\vec r)e^{-j\omega t} \\ E(r,t)=E(r)e−jωtH(r,t)=H(r)e−jωt
-
光波导一般不存在自由电荷: ρ = 0 \rho=0 ρ=0
-
光波导一般不存在自由电流: J ⃗ = 0 \vec J=0 J=0
-
光波导材料一般无磁性: μ = μ 0 \mu=\mu_0 μ=μ0
结合上述条件,得到亥姆霍兹方程为:
∇
2
E
⃗
+
k
2
E
⃗
+
∇
(
E
⃗
⋅
∇
ε
ε
)
=
0
(1-1)
\nabla^2\vec E+k^2\vec E+\nabla(\vec E\cdot\frac{\nabla \varepsilon}{\varepsilon})=0 \tag{1-1}
∇2E+k2E+∇(E⋅ε∇ε)=0(1-1)
∇
2
H
⃗
+
k
2
H
⃗
+
∇
ε
ε
×
(
∇
×
H
⃗
)
=
0
(1-1)
\nabla^2\vec H+k^2\vec H+\frac{\nabla \varepsilon}{\varepsilon}\times(\nabla\times\vec H)=0 \tag{1-1}
∇2H+k2H+ε∇ε×(∇×H)=0(1-1)
1.3 正规光波导中模式场的亥姆霍兹方程及模式的概念
正规光波导
-
折射率沿纵向不变的一种波导
-
电容率可以写成: ε ( x , y , z ) = ε ( x , y ) \varepsilon(x,y,z)=\varepsilon(x,y) ε(x,y,z)=ε(x,y)
-
导波场可以写成:
E
⃗
(
x
,
y
,
z
)
=
E
⃗
(
x
,
y
)
e
−
j
β
z
(1-2)
\vec E(x,y,z)=\vec E(x,y)e^{-j\beta z} \tag{1-2}
E(x,y,z)=E(x,y)e−jβz(1-2)
H
⃗
(
x
,
y
,
z
)
=
H
⃗
(
x
,
y
)
e
−
j
β
z
(1-2)
\vec H(x,y,z)=\vec H(x,y)e^{-j\beta z} \tag{1-2}
H(x,y,z)=H(x,y)e−jβz(1-2)
β \beta β 称为传播系数,反应导波在波导内的传播速度
模式场的亥姆霍兹方程
将正规光纤中的导波场(1-2)代入亥姆霍兹方程(1-1),可以得到模式场的亥姆霍兹方程(1-3):
∇
t
2
E
⃗
(
x
,
y
)
+
(
k
0
2
n
2
−
β
2
)
E
⃗
(
x
,
y
)
+
∇
t
[
E
⃗
(
x
,
y
)
⋅
∇
t
ε
ε
]
+
j
β
[
E
⃗
(
x
,
y
)
⋅
∇
t
ε
ε
]
z
^
=
0
(1-3)
\nabla^2_t\vec E(x,y)+(k^2_0n^2-\beta^2)\vec E(x,y)+\nabla_t\left[ \vec E(x,y)\cdot\frac{\nabla_t \varepsilon}{\varepsilon} \right]+j\beta\left[ \vec E(x,y)\cdot\frac{\nabla_t \varepsilon}{\varepsilon} \right]\hat z=0 \tag{1-3}
∇t2E(x,y)+(k02n2−β2)E(x,y)+∇t[E(x,y)⋅ε∇tε]+jβ[E(x,y)⋅ε∇tε]z^=0(1-3)
∇
t
2
H
⃗
(
x
,
y
)
+
(
k
0
2
n
2
−
β
2
)
H
⃗
(
x
,
y
)
+
∇
t
ε
ε
×
[
∇
t
×
H
⃗
(
x
,
y
)
]
+
j
β
[
H
⃗
(
x
,
y
)
⋅
∇
t
ε
ε
]
z
^
=
0
(1-3)
\nabla^2_t\vec H(x,y)+(k^2_0n^2-\beta^2)\vec H(x,y)+\frac{\nabla_t \varepsilon}{\varepsilon}\times\left[ \nabla_t\times\vec H(x,y) \right]+j\beta\left[ \vec H(x,y)\cdot\frac{\nabla_t \varepsilon}{\varepsilon} \right]\hat z=0 \tag{1-3}
∇t2H(x,y)+(k02n2−β2)H(x,y)+ε∇tε×[∇t×H(x,y)]+jβ[H(x,y)⋅ε∇tε]z^=0(1-3)
根据式(1-3),由偏微分方程相关理论可知:
- 在给定边界条件下,可以得到一个个离散的特征解
- 每个特征解与一个特征值相对应
- 通解是这些特征解的线性叠加
- 给定初始条件时,可以确定特征解的系数
模式的概念
- 一个特征解就是一个光波导的模式
- 数学上,模式是满足式(1-3)及边界条件的一个特解
- 物理上,模式是正规光波导中光波的一种可能的存在形式;模式场是正规光波导的光场在横截面上的一种可能的场分布
1.4 模式场横、纵向分量的关系
横向分量: x − y x-y x−y 平面内的分量为横向分量,记 E ⃗ t \vec E_t Et、 H ⃗ t \vec H_t Ht
纵向分量: z z z 方向的分量为纵向分量,记 E ⃗ z \vec E_z Ez、 H ⃗ z \vec H_z Hz
拆分微分算子: ∇ = ∇ t + ∂ ∂ z \nabla=\nabla_t+\frac{\partial}{\partial z} ∇=∇t+∂z∂
模式场的横向分量可用纵向分量表示
结合单色光、线性、静止、各向同性介质的物质方程,可以得到单频电磁场的麦克斯韦方程组。将其横、纵电磁场拆分,进一步推到可以得到:
E
⃗
t
(
x
,
y
)
=
j
ω
2
μ
0
ε
−
β
2
[
−
ω
μ
0
z
^
×
∇
t
H
⃗
z
(
x
,
y
)
+
β
∇
t
E
⃗
z
(
x
,
y
)
]
(1-4)
\vec E_t(x,y)=\frac{j}{\omega^2\mu_0\varepsilon-\beta^2}\left[ -\omega\mu_0\hat z\times\nabla_t\vec H_z(x,y)+\beta\nabla_t\vec E_z(x,y) \right] \tag{1-4}
Et(x,y)=ω2μ0ε−β2j[−ωμ0z^×∇tHz(x,y)+β∇tEz(x,y)](1-4)
H
⃗
t
(
x
,
y
)
=
j
ω
2
μ
0
ε
−
β
2
[
ω
μ
0
z
^
×
∇
t
E
⃗
z
(
x
,
y
)
+
β
∇
t
H
⃗
z
(
x
,
y
)
]
(1-4)
\vec H_t(x,y)=\frac{j}{\omega^2\mu_0\varepsilon-\beta^2}\left[ \omega\mu_0\hat z\times\nabla_t\vec E_z(x,y)+\beta\nabla_t\vec H_z(x,y) \right] \tag{1-4}
Ht(x,y)=ω2μ0ε−β2j[ωμ0z^×∇tEz(x,y)+β∇tHz(x,y)](1-4)
1.5 模式的正交性与模式展开
正/反向模模式场的关系
正向模:沿 z z z 方向传播的模式,记 E ⃗ ( x , y ) \vec E(x,y) E(x,y), H ⃗ ( x , y ) \vec H(x,y) H(x,y)
反向模:沿 − z -z −z 方向传播的模式,记 E ⃗ ~ ( x , y ) \widetilde{ \vec E}(x,y) E (x,y), H ⃗ ~ ( x , y ) \widetilde{\vec H}(x,y) H (x,y)
反向模与正向模相比,仅有 β \beta β 变为 − β -\beta −β
根据模式场的亥姆霍兹方程(1-3)可知,反向模的横向分量满足的亥姆霍兹方程与正向模相同。即方程的解相同或差一个负号:
- E ⃗ ~ t ( x , y ) = ± E ⃗ t ( x , y ) \widetilde{ \vec E}_t(x,y)=\pm\vec E_t(x,y) E t(x,y)=±Et(x,y)
- H ⃗ ~ t ( x , y ) = ± H ⃗ t ( x , y ) \widetilde{ \vec H}_t(x,y)=\pm\vec H_t(x,y) H t(x,y)=±Ht(x,y)
由于正反模能流方向相反,有:
- E ⃗ ~ t ( x , y ) × H ⃗ ~ t ( x , y ) = − E ⃗ ( x , y ) × H ⃗ ( x , y ) \widetilde{ \vec E}_t(x,y)\times\widetilde{\vec H}_t(x,y)=-\vec E(x,y)\times\vec H(x,y) E t(x,y)×H t(x,y)=−E(x,y)×H(x,y)
即分为两种情况:
| E ⃗ t \vec E_t Et | H ⃗ t \vec H_t Ht | E ⃗ z \vec E_z Ez | H ⃗ z \vec H_z Hz | |
|---|---|---|---|---|
| 情况一 | E ⃗ ~ t ( x , y ) = E ⃗ t ( x , y ) \widetilde{ \vec E}_t(x,y)=\vec E_t(x,y) E t(x,y)=Et(x,y) | H ⃗ ~ t ( x , y ) = − H ⃗ t ( x , y ) \widetilde{ \vec H}_t(x,y)=-\vec H_t(x,y) H t(x,y)=−Ht(x,y) | E ⃗ ~ z ( x , y ) = E ⃗ z ( x , y ) \widetilde{ \vec E}_z(x,y)=\vec E_z(x,y) E z(x,y)=Ez(x,y) | H ⃗ ~ z ( x , y ) = − H ⃗ z ( x , y ) \widetilde{ \vec H}_z(x,y)=-\vec H_z(x,y) H z(x,y)=−Hz(x,y) |
| 情况二 | E ⃗ ~ t ( x , y ) = − E ⃗ t ( x , y ) \widetilde{ \vec E}_t(x,y)=-\vec E_t(x,y) E t(x,y)=−Et(x,y) | H ⃗ ~ t ( x , y ) = H ⃗ t ( x , y ) \widetilde{ \vec H}_t(x,y)=\vec H_t(x,y) H t(x,y)=Ht(x,y) | E ⃗ ~ z ( x , y ) = − E ⃗ z ( x , y ) \widetilde{ \vec E}_z(x,y)=-\vec E_z(x,y) E z(x,y)=−Ez(x,y) | H ⃗ ~ z ( x , y ) = H ⃗ z ( x , y ) \widetilde{ \vec H}_z(x,y)=\vec H_z(x,y) H z(x,y)=Hz(x,y) |
模式的正交性
正规光波导中,两种模式分别记为
μ
\mu
μ,
ν
\nu
ν。经推导可得:
∬
−
∞
∞
[
E
⃗
t
μ
(
x
,
y
)
×
H
⃗
t
ν
∗
(
x
,
y
)
]
⋅
z
^
d
x
d
y
=
0
β
μ
≠
β
ν
∬
−
∞
∞
[
E
⃗
t
ν
∗
(
x
,
y
)
×
H
⃗
t
μ
(
x
,
y
)
]
⋅
z
^
d
x
d
y
=
0
β
μ
≠
β
ν
\iint_{-\infty}^{\infty}\left[ \vec E_{t\mu}(x,y)\times\vec H_{t\nu}^*(x,y) \right]\cdot\hat zdxdy=0\quad \beta_\mu\neq\beta_\nu \\ \iint_{-\infty}^{\infty}\left[ \vec E_{t\nu}^*(x,y)\times\vec H_{t\mu}(x,y) \right]\cdot\hat zdxdy=0\quad \beta_\mu\neq\beta_\nu \\
∬−∞∞[Etμ(x,y)×Htν∗(x,y)]⋅z^dxdy=0βμ=βν∬−∞∞[Etν∗(x,y)×Htμ(x,y)]⋅z^dxdy=0βμ=βν
∗
^*
∗ 表示取复共轭。上式证明了正规光波导中,模式与模式相互正交。即
- 如果 μ \mu μ、 ν \nu ν 均为导模,则两模式正交
- 如果 μ \mu μ、 ν \nu ν 中,一个是导模,一个是辐射模,两模式依然正交(涉及辐射模的振荡性质,暂不证明)
模式的归一化与模式的展开
模式展开:
- 因为模式之间相互正交,所以可以用模式作为基矢量,将波导中的任意场分布的横向分量表示为模式场横向分量的线性叠加,即(
a
a
a 为展开系数):
- E ⃗ t ( x , y ) = ∑ μ a μ E ⃗ t μ ( x , y ) \vec E_t(x,y)=\sum_\mu a_\mu \vec E_{t\mu}(x,y) Et(x,y)=∑μaμEtμ(x,y)
- H ⃗ t ( x , y ) = ∑ μ a μ H ⃗ t μ ( x , y ) \vec H_t(x,y)=\sum_\mu a_\mu \vec H_{t\mu}(x,y) Ht(x,y)=∑μaμHtμ(x,y)
- 由于辐射模不能在波导中持续传播,所以在模式展开中忽略
- 通常把波导中的模式场归一化(功率为1),使之成为正交、归一化的基矢量
- P = 1 2 ∬ − ∞ ∞ [ E ⃗ ( x , y ) × H ⃗ ∗ ( x , y ) ] ⋅ z ^ d x d y P=\frac12\iint_{-\infty}^\infty\left[ \vec E(x,y)\times\vec H^*(x,y) \right]\cdot\hat zdxdy P=21∬−∞∞[E(x,y)×H∗(x,y)]⋅z^dxdy
- 任意 z z z 方向传播的场所携带的总功率 = 各模式场所携带的功率之和
- 波导中,沿
z
z
z 轴传播的任意电磁场同样可以展开。其中
c
μ
(
z
)
c_\mu(z)
cμ(z)、
d
μ
(
z
)
d_\mu(z)
dμ(z) 之所以不同且随
z
z
z 变化,是考虑到波导不同模式之间可能存在耦合
- E ⃗ ( x , y , z ) = ∑ μ c μ ( z ) E ⃗ μ ( x , y ) e x p ( j β μ z ) \vec E(x,y,z)=\sum_\mu c_\mu(z) \vec E_{\mu}(x,y)exp(j\beta_\mu z) E(x,y,z)=∑μcμ(z)Eμ(x,y)exp(jβμz)
- H ⃗ ( x , y , z ) = ∑ μ d μ ( z ) H ⃗ μ ( x , y ) e x p ( j β μ z ) \vec H(x,y,z)=\sum_\mu d_\mu(z) \vec H_{\mu}(x,y)exp(j\beta_\mu z) H(x,y,z)=∑μdμ(z)Hμ(x,y)exp(jβμz)
二、光在介质中的传播特性
2.1 反射、折射、全反射
光在通过两种不同介质的分界面时,会发生反射与折射现象。假设入射、反射光均为理想平面波且具有单一波长。
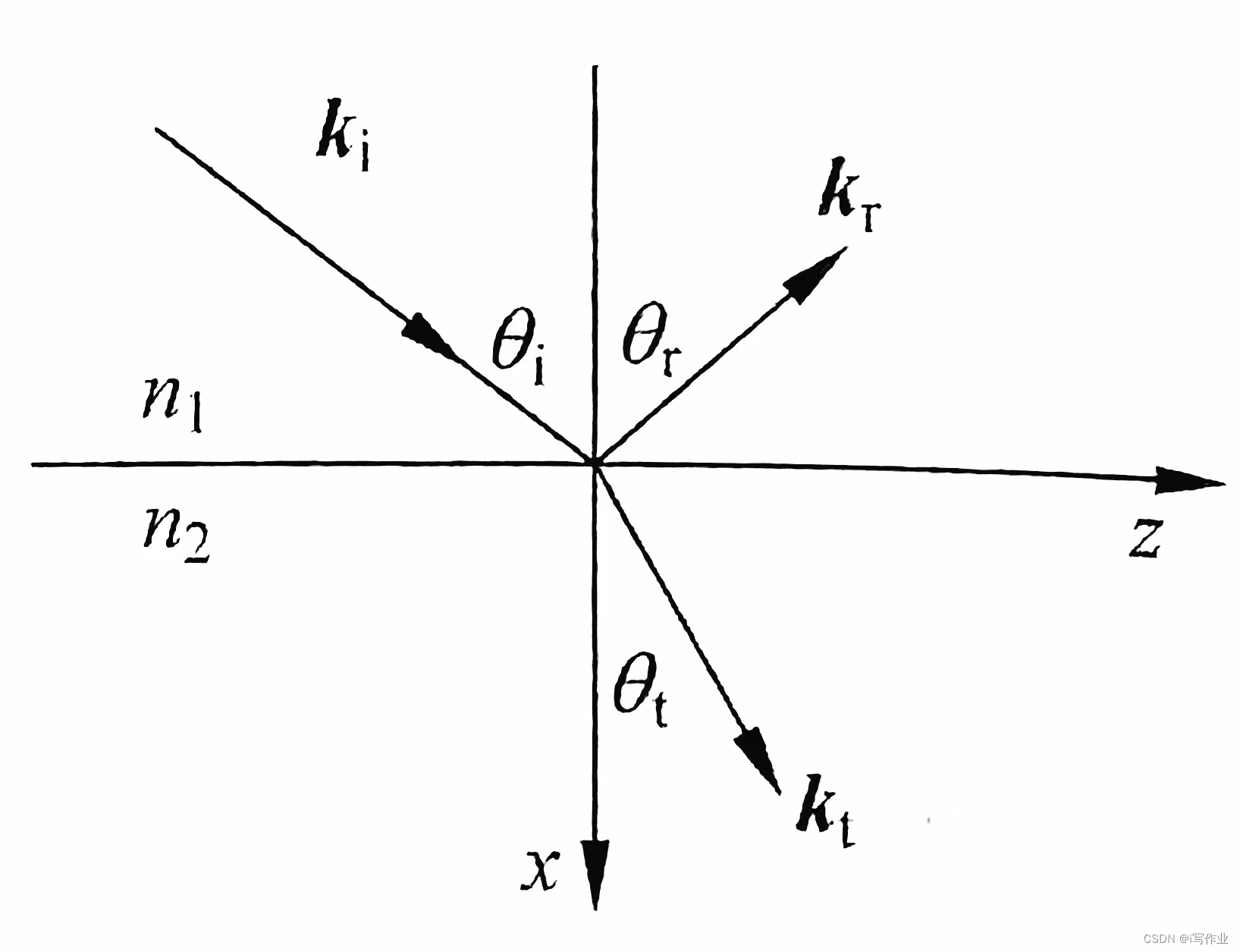
入射光、折射光、反射光的表示方式
入射光:
- E ⃗ 0 e x p ( j ( k ⃗ i ⋅ r ⃗ − ω i t ) ) \vec E_0 exp(j(\vec k_i\cdot\vec r-\omega_it)) E0exp(j(ki⋅r−ωit))
- H ⃗ 0 e x p ( j ( k ⃗ i ⋅ r ⃗ − ω i t ) ) \vec H_0 exp(j(\vec k_i\cdot\vec r-\omega_it)) H0exp(j(ki⋅r−ωit))
反射光:
- E ⃗ 0 ′ e x p ( j ( k ⃗ r ⋅ r ⃗ − ω i t ) ) \vec E_0^\prime exp(j(\vec k_r\cdot\vec r-\omega_it)) E0′exp(j(kr⋅r−ωit))
- H ⃗ 0 ′ e x p ( j ( k ⃗ r ⋅ r ⃗ − ω i t ) ) \vec H_0^\prime exp(j(\vec k_r\cdot\vec r-\omega_it)) H0′exp(j(kr⋅r−ωit))
折射光:
- E ⃗ 0 ′ ′ e x p ( j ( k ⃗ t ⋅ r ⃗ − ω i t ) ) \vec E_0^{\prime\prime} exp(j(\vec k_t\cdot\vec r-\omega_it)) E0′′exp(j(kt⋅r−ωit))
- H ⃗ 0 ′ ′ e x p ( j ( k ⃗ t ⋅ r ⃗ − ω i t ) ) \vec H_0^{\prime\prime} exp(j(\vec k_t\cdot\vec r-\omega_it)) H0′′exp(j(kt⋅r−ωit))
不同介质间界面的边界条件
边界处 E ⃗ \vec E E、 H ⃗ \vec H H 可以得到的边界条件:
- ω i = ω r = ω t \omega_i=\omega_r=\omega_t ωi=ωr=ωt
- θ i = θ r = θ 1 \theta_i=\theta_r=\theta_1 θi=θr=θ1; n 1 sin θ 1 = n 2 sin θ 2 n_1\sin\theta_1=n_2\sin\theta_2 n1sinθ1=n2sinθ2, ( θ t = θ 2 ) (\theta_t=\theta_2) (θt=θ2)
- 入射波、反射波在同一平面内
菲涅尔(Fresnel)公式
由边界条件可以导出菲涅尔(Fresnel)公式。用 r r r 表示入射波与反射波振幅的比值
- 对于 TE 模偏振( E ⃗ \vec E E 垂直于入射面)的波:
r T E = E ⃗ 0 ′ E ⃗ 0 = n 1 cos θ 1 − n 2 2 − n 1 2 s i n 2 θ 1 n 1 cos θ 1 + n 2 2 − n 1 2 s i n 2 θ 1 (2-1) r_{TE}=\frac{\vec E_0^\prime}{\vec E_0}=\frac {n_1\cos\theta_1-\sqrt{n_2^2-n_1^2sin^2\theta_1}} {n_1\cos\theta_1+\sqrt{n_2^2-n_1^2sin^2\theta_1}} \tag{2-1} rTE=E0E0′=n1cosθ1+n22−n12sin2θ1n1cosθ1−n22−n12sin2θ1(2-1)
- 对于 TM 模偏振( M ⃗ \vec M M 垂直于入射面)的波:
r T M = H ⃗ 0 ′ H ⃗ 0 = n 2 2 cos θ 1 − n 1 n 2 2 − n 1 2 s i n 2 θ 1 n 2 2 cos θ 1 + n 1 n 2 2 − n 1 2 s i n 2 θ 1 (2-2) r_{TM}=\frac{\vec H_0^\prime}{\vec H_0}=\frac {n_2^2\cos\theta_1-n_1\sqrt{n_2^2-n_1^2sin^2\theta_1}} {n_2^2\cos\theta_1+n_1\sqrt{n_2^2-n_1^2sin^2\theta_1}} \tag{2-2} rTM=H0H0′=n22cosθ1+n1n22−n12sin2θ1n22cosθ1−n1n22−n12sin2θ1(2-2)
- 其中一个特例——当 θ 1 = 0 \theta_1=0 θ1=0 时,TE、TM偏振的入射-反射振幅比值相同,相位差 π \pi π
r T E = − r T M = n 1 − n 2 n 1 + n 2 r_{TE}=-r_{TM}=\frac{n_1-n_2}{n_1+n_2} rTE=−rTM=n1+n2n1−n2
全反射时折射光的能流
- 全反射时,能量并非不进入 n 2 n_2 n2 介质。只是某个半周期内,能流流入 n 2 n_2 n2 介质,而另一个半周期内,能流又从 n 2 n_2 n2 介质流回来。最终平均能流为 0
- 进入 n 2 n_2 n2 介质的折射光电磁场按指数规律衰减,折射光平均能流为 0,这种电磁场成为消逝场
- 全反射临界角 sin θ c = n 2 / n 1 \sin \theta_c=n_2/n_1 sinθc=n2/n1
反射光的相移
由(2-1)、(2-2)可得:
- 若 θ 1 < θ c \theta_1<\theta_c θ1<θc, r < 1 r<1 r<1,说明光被部分反射,且没有发生相移
- 若 θ 1 > θ c \theta_1>\theta_c θ1>θc,讲(2-1)、(2-2)变换为虚指数形式有:
r T E = E ⃗ 0 ′ E ⃗ 0 = n 1 cos θ 1 − n 2 2 − n 1 2 s i n 2 θ 1 n 1 cos θ 1 + n 2 2 − n 1 2 s i n 2 θ 1 = e x p [ − j 2 arctan ( n 1 2 sin 2 θ 1 − n 2 2 n 1 cos θ 1 ) ] = e − j 2 ϕ T E r_{TE}=\frac{\vec E_0^\prime}{\vec E_0}=\frac {n_1\cos\theta_1-\sqrt{n_2^2-n_1^2sin^2\theta_1}} {n_1\cos\theta_1+\sqrt{n_2^2-n_1^2sin^2\theta_1}} =exp\left[ {-j2\arctan\left( \frac{\sqrt{n_1^2\sin^2\theta_1-n_2^2}}{n_1\cos\theta_1} \right)} \right] =e^{-j2\phi_{TE}} rTE=E0E0′=n1cosθ1+n22−n12sin2θ1n1cosθ1−n22−n12sin2θ1=exp −j2arctan n1cosθ1n12sin2θ1−n22 =e−j2ϕTE
r T M = H ⃗ 0 ′ H ⃗ 0 = n 2 2 cos θ 1 − n 1 n 2 2 − n 1 2 s i n 2 θ 1 n 2 2 cos θ 1 + n 1 n 2 2 − n 1 2 s i n 2 θ 1 = e x p [ − j 2 arctan ( n 1 2 n 2 2 n 1 2 sin 2 θ 1 − n 2 2 n 1 cos θ 1 ) ] = e − j 2 ϕ T M r_{TM}=\frac{\vec H_0^\prime}{\vec H_0}=\frac {n_2^2\cos\theta_1-n_1\sqrt{n_2^2-n_1^2sin^2\theta_1}} {n_2^2\cos\theta_1+n_1\sqrt{n_2^2-n_1^2sin^2\theta_1}} =exp\left[ {-j2\arctan\left( \frac{n_1^2}{n_2^2}\frac{\sqrt{n_1^2\sin^2\theta_1-n_2^2}}{n_1\cos\theta_1} \right)} \right] =e^{-j2\phi_{TM}} rTM=H0H0′=n22cosθ1+n1n22−n12sin2θ1n22cosθ1−n1n22−n12sin2θ1=exp −j2arctan n22n12n1cosθ1n12sin2θ1−n22 =e−j2ϕTM
可以看到此时 ∣ r T E ∣ = ∣ r T M ∣ = 1 |r_{TE}|=|r_{TM}|=1 ∣rTE∣=∣rTM∣=1,即光被全部反射,且反射光产生相移 2 ϕ r T E 2\phi r_{TE} 2ϕrTE 或 2 ϕ r T M 2\phi r_{TM} 2ϕrTM
2.2 古斯-汉欣(Goos-Hänchen)位移
对于实际的光线,1947年古斯-汉欣曾做过实验,证明反射点与入射点间具有一段位移。此位移成为古斯-汉欣位移,与 θ 1 \theta_1 θ1、 n 1 n_1 n1、 n 2 n_2 n2、 λ \lambda λ 有关
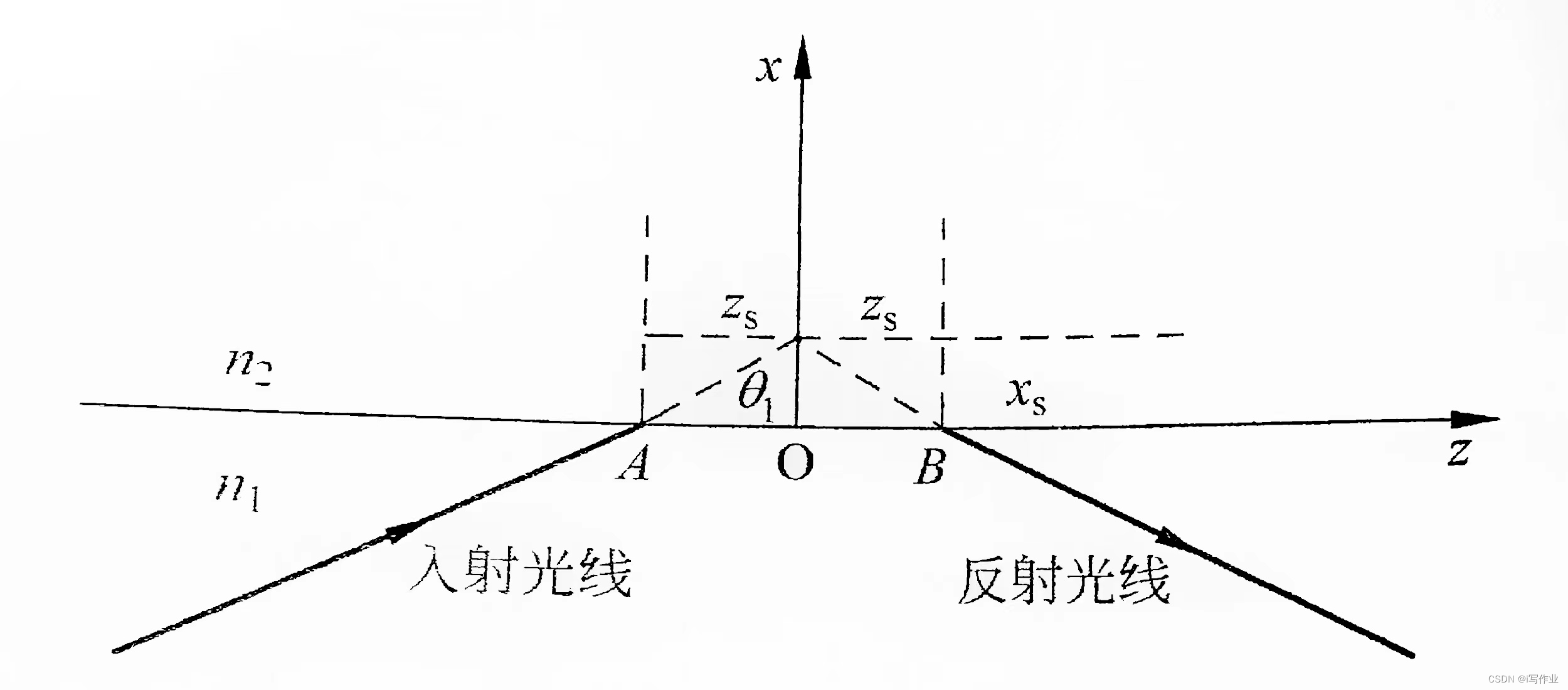
基于实际的空间光具有一定的宽度(而不是平面电磁波),推导出 TE、TM 波的古斯-汉欣位移的 1/2 为:
z
s
=
{
tan
θ
1
α
T
E
波
n
2
2
n
1
2
sin
2
θ
1
−
n
2
2
cos
2
θ
1
tan
θ
1
α
T
M
波
z_s= \begin{cases} \frac{\tan\theta_1}{\alpha} &TE波 \\ \frac{n_2^2}{n_1^2\sin^2\theta_1-n_2^2\cos^2\theta_1} \frac{\tan\theta_1}{\alpha} &TM波 \\ \end{cases}
zs={αtanθ1n12sin2θ1−n22cos2θ1n22αtanθ1TE波TM波
式中
α
=
k
0
n
1
2
sin
2
θ
1
−
n
2
2
\alpha=k_0\sqrt{n_1^2\sin^2\theta_1-n_2^2}
α=k0n12sin2θ1−n22
光线进入
n
2
n_2
n2 介质的深度
x
s
x_s
xs 为:
x
s
=
z
s
/
tan
θ
1
=
{
1
α
T
E
波
n
2
2
n
1
2
sin
2
θ
1
−
n
2
2
cos
2
θ
1
1
α
T
M
波
x_s=z_s/\tan\theta_1= \begin{cases} \frac{1}{\alpha} &TE波 \\ \frac{n_2^2}{n_1^2\sin^2\theta_1-n_2^2\cos^2\theta_1} \frac{1}{\alpha} &TM波 \\ \end{cases}
xs=zs/tanθ1={α1n12sin2θ1−n22cos2θ1n22α1TE波TM波
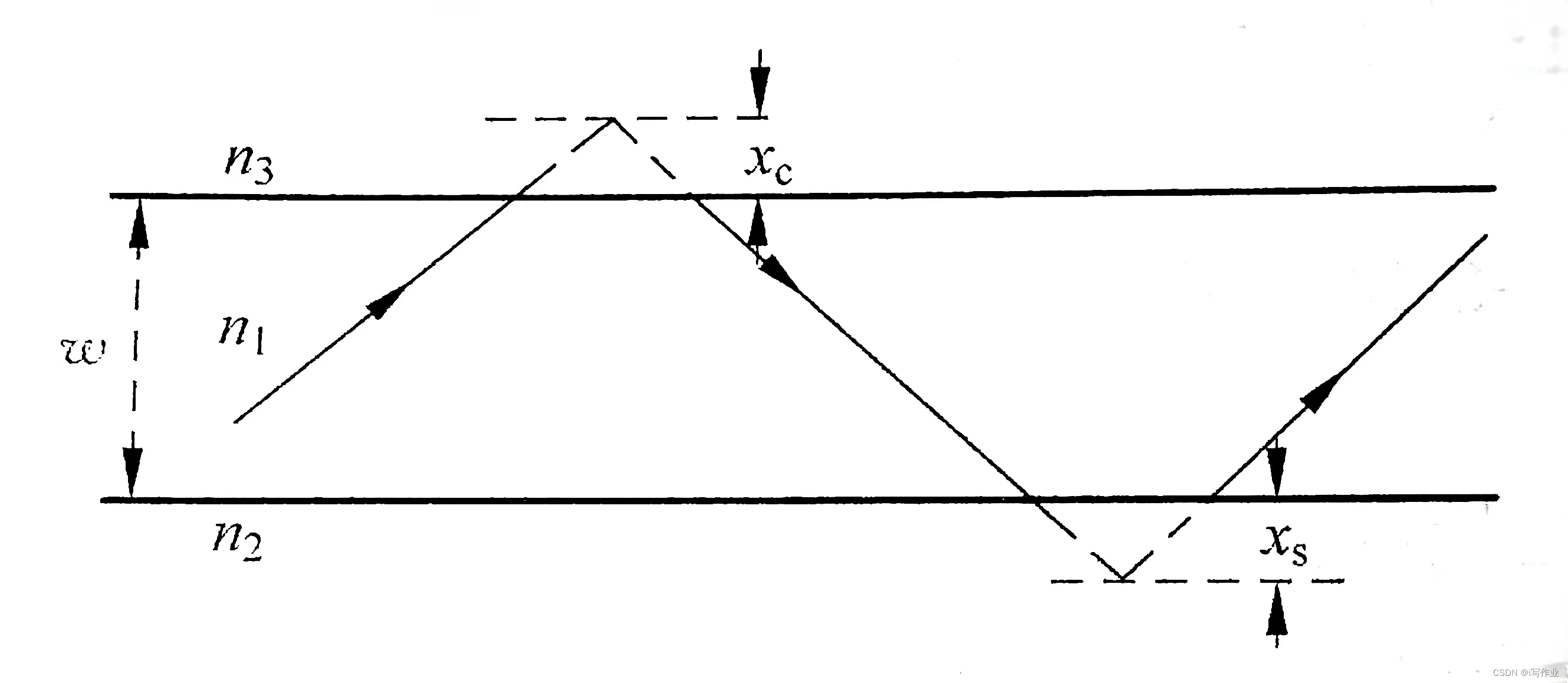
由于古斯-汉欣位移的存在,光线在三层平板波导中的传播轨迹如上图所示。可以看到:
- 波导芯区的有效厚度比实际厚度增加了
2.3 射线光学基础
前面对反射、折射、全反射、古斯-汉欣位移的分析,是在以下几个条件下分析的:
- 在均匀介质界面上
- 均匀波导
- 均匀平面电磁波
- 单频光
但是面对非均匀介质中传播的情况则无能为力了。为此下面讨论在非均匀介质中传播的情况
程函(eikonal)方程
在非均匀介质中,折射率是空间位置的函数,因此需要新的描述电磁场的方程:
- E ⃗ ( r ⃗ ) = E ⃗ 0 ( r ⃗ ) e j k 0 φ ( r ⃗ ) \vec E(\vec r)=\vec E_0(\vec r)e^{jk_0\varphi(\vec r)} E(r)=E0(r)ejk0φ(r)
- H ⃗ ( r ⃗ ) = H ⃗ 0 ( r ⃗ ) e j k 0 φ ( r ⃗ ) \vec H(\vec r)=\vec H_0(\vec r)e^{jk_0\varphi(\vec r)} H(r)=H0(r)ejk0φ(r)
这里振幅矢量 E ⃗ 0 ( r ⃗ ) \vec E_0(\vec r) E0(r)、 H ⃗ 0 ( r ⃗ ) \vec H_0(\vec r) H0(r) 都是位置的函数
φ
(
r
⃗
)
\varphi(\vec r)
φ(r) 称为光程函数,代表光射线的相位特性,在各向同性的介质中:
φ
(
r
)
=
∫
n
(
r
)
d
s
\varphi(r)=\int n(r)ds
φ(r)=∫n(r)ds
这里
n
(
r
)
n(r)
n(r) 表示各点的折射率,
d
s
ds
ds 表示光所走的微小路程
光程=折射率×距离,即将光在介质中走过的路程,通过折射率折算到真空中光走过的路程进行比较
程函方程:
∣
∇
φ
(
r
⃗
)
∣
=
n
(
r
⃗
)
(程函方程)
|\nabla\varphi(\vec r)|=n(\vec r) \tag{程函方程}
∣∇φ(r)∣=n(r)(程函方程)
此方程表明:
- 电场矢量、磁场矢量与等相位面/等光程面的法向量垂直,所以在非均匀介质中,波长极短的电磁波与平面电磁波一样,仍是横电磁波或TEM波
- 介质中各点电磁波的最大相位变化与该点的折射率成正比
射线方程
程函方程本身不能直接帮我们求解射线所走的路径,因此从程函方程推导出射线所遵循的方程——射线方程
此方程为
r
⃗
\vec r
r 的二阶微分方程,称为射线方程。在给定
n
(
r
⃗
)
n(\vec r)
n(r) 的分布及坐标的情况下,由初始条件就可以推出射线路径。
d
d
s
[
d
r
⃗
d
s
n
(
r
⃗
)
]
=
∇
n
(
r
⃗
)
(射线方程)
\frac d{ds}\left[ \frac{d\vec r}{ds}n(\vec r) \right]=\nabla n(\vec r) \tag{射线方程}
dsd[dsdrn(r)]=∇n(r)(射线方程)
射线总是向介质折射率增大的方向弯曲