6.6 Differentiating trigonometric functions(反三角函数求导)
Edexcel Pure Mathematics 3(2018版本教材)
/--------------------------------------------------------------------------------------------------------------------
Prior Knowledge(预备知识温习)
①
(
s
i
n
x
)
′
=
c
o
s
x
+
C
(sinx)'=cosx+C
(sinx)′=cosx+C
②
(
c
o
s
x
)
′
=
−
s
i
n
x
+
C
(cosx)'=-sinx+C
(cosx)′=−sinx+C
③
(
u
v
)
′
=
u
′
v
−
v
′
u
v
2
(\frac{u}{v})'=\frac{u'v-v'u}{v^2}
(vu)′=v2u′v−v′u
④三角形六边形法则-对角线上 两个函数互为倒数
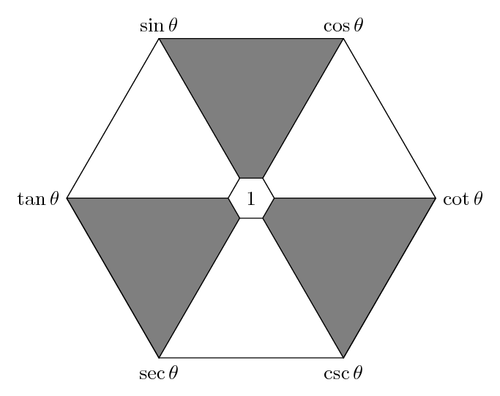
对角线上 两个函数互为倒数
根据上述知识,我们下面看一道 习题
Example 14
If
y
=
k
⋅
t
a
n
x
y=k·tanx
y=k⋅tanx,find
d
y
d
x
\frac{dy}{dx}
dxdy
Solution:
y
=
k
tan
x
=
k
sin
x
cos
x
Let
u
=
sin
x
v
=
cos
x
d
u
d
x
=
cos
x
and
d
v
d
x
=
−
sin
x
d
y
d
x
=
k
v
d
u
d
x
−
u
d
v
d
x
v
2
=
k
cos
x
×
cos
x
−
sin
x
(
−
sin
x
)
cos
2
x
=
k
cos
2
x
+
sin
2
x
cos
2
x
=
k
1
cos
2
x
=
k
sec
2
x
\begin{array}{l} y=k\tan x=k\frac{\sin x}{\cos x} \\ \text { Let } u=\sin x \text v=\cos x \\ \qquad \begin{aligned} \frac{d u}{d x} & =\cos x \text { and } \frac{d v}{d x}=-\sin x \\ \frac{d y}{d x} & =k\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^{2}} \\ & =k\frac{\cos x \times \cos x-\sin x(-\sin x)}{\cos ^{2} x} \\ & =k\frac{\cos ^{2} x+\sin ^{2} x}{\cos ^{2} x} \\ & =k\frac{1}{\cos ^{2} x}=k\sec ^{2} x \end{aligned} \end{array}
y=ktanx=kcosxsinx Let u=sinxv=cosxdxdudxdy=cosx and dxdv=−sinx=kv2vdxdu−udxdv=kcos2xcosx×cosx−sinx(−sinx)=kcos2xcos2x+sin2x=kcos2x1=ksec2x
Prior Knowledge(预备知识温习)
(
u
v
)
′
=
u
′
v
+
u
v
′
(uv)'=u'v+uv'
(uv)′=u′v+uv′
(
t
a
n
x
)
′
=
s
e
c
2
x
(tanx)'=sec^2x
(tanx)′=sec2x
Example 15
y
=
x
tan
2
x
y=x\tan2x
y=xtan2x
=
x
×
2
sec
2
2
x
+
tan
2
x
=x\times2\sec^{2}2x+\tan2x
=x×2sec22x+tan2x
=
2
x
sec
2
2
x
+
tan
2
x
=2x\sec^{2}2x+\tan2x
=2xsec22x+tan2x
y
=
tan
4
x
=
(
tan
x
)
4
y=\tan^4x=(\tan x)^4
y=tan4x=(tanx)4
d
y
d
x
=
4
(
tan
x
)
3
(
sec
2
x
)
\frac{dy}{dx}=4(\tan x)^{3}(\sec^{2}x)
dxdy=4(tanx)3(sec2x)
=
4
tan
3
x
sec
2
x
=4\tan^{3}x\sec^{2}x
=4tan3xsec2x
Prior Knowledge(预备知识温习)
1
c
o
s
e
c
x
=
1
s
i
n
x
(
三角形六边形法则
)
\frac{1}{cosecx}=\frac{1}{sinx}(三角形六边形 法则)
cosecx1=sinx1(三角形六边形法则)
(
u
v
)
′
=
u
′
v
−
v
′
u
v
2
(\frac{u}{v})'=\frac{u'v-v'u}{v^2}
(vu)′=v2u′v−v′u
Example 16
y
=
c
o
s
e
c
x
=
1
sin
x
L
e
t
u
=
1
a
n
d
v
=
sin
x
d
u
d
x
=
0
a
n
d
d
v
d
x
=
cos
x
\begin{aligned}y&=\mathrm{cosec~}x=\frac1{\sin x}\\\mathrm{Let~}u&=1\mathrm{~and~}v=\sin x\\\frac{du}{dx}&=0\mathrm{~and~}\frac{dv}{dx}=\cos x\end{aligned}
yLet udxdu=cosec x=sinx1=1 and v=sinx=0 and dxdv=cosx
d y d x = v d u d x − u d v d x v 2 = sin x × 0 − 1 × cos x sin 2 x = − cos x sin 2 x = − 1 sin x × cos x sin x = − cosec x cot x \begin{aligned} \frac{dy}{dx}& =\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2} \\ &=\frac{\sin x\times0-1\times\cos x}{\sin^2x} \\ &=-\frac{\cos x}{\sin^2x} \\ &=-\frac1{\sin x}\times\frac{\cos x}{\sin x}=-\cosec x\cot x \end{aligned} dxdy=v2vdxdu−udxdv=sin2xsinx×0−1×cosx=−sin2xcosx=−sinx1×sinxcosx=−cosecxcotx
Extension
If y=
s
e
c
k
x
seckx
seckx,find
d
y
d
x
\frac{dy}{dx}
dxdy
d
y
d
x
=
(
1
c
o
s
k
x
)
′
1
′
c
o
s
k
x
−
(
c
o
s
k
x
)
′
⋅
1
c
o
s
2
k
x
=
−
k
(
−
s
i
n
k
x
)
c
o
s
2
k
x
=
=
k
1
c
o
s
k
x
s
i
n
k
x
c
o
s
k
x
=
k
⋅
s
e
c
k
x
⋅
t
a
n
k
x
\frac{dy}{dx}=(\frac{1}{coskx})'\\ \\ \frac{1'coskx-(coskx)'·1}{cos^2kx}\\ =\frac{-k(-sinkx)}{cos^2kx}=\\ =k\frac{1}{coskx}\frac{sinkx}{coskx}\\ =k·seckx·tankx
dxdy=(coskx1)′cos2kx1′coskx−(coskx)′⋅1=cos2kx−k(−sinkx)==kcoskx1coskxsinkx=k⋅seckx⋅tankx
Example 17