目录

基本概念

定义

分类：

数学模型

 分为

 整数规划和松弛的线性规划的关系​编辑

---

基本概念

定义

数学规划中变量限制为整数时，称为整数规划

线性规划中变量限制为整数时，称为整数线性规划

分类：

变量全限制为整数时，称纯（完全）整数规划

变量部分限制为整数时，称混合整数规划

特点：

原线性规划有最优解，当自变量限制为整数后，其整数规划出现下述情况

1. 最优解全为整数，则整数规划最优解与线性规划最优解一致
2. 整数规划无可行解（解都有小数）
3. 有可行解，但最优解值变差（有可以的点，但无法取到最优解）

数学模型

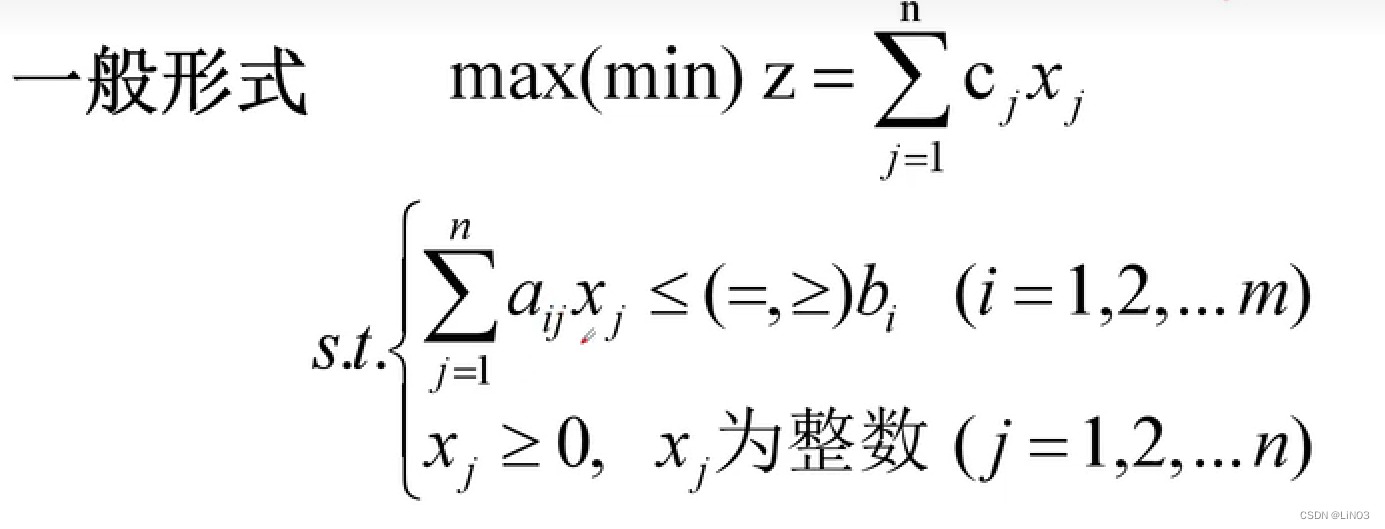
 分为

 整数规划和松弛的线性规划的关系

关系

整数规划可行域是松弛的整数格数

松弛无可行解，整数规划必没有可行解

整数规划的最优解小于等于松弛的最优解