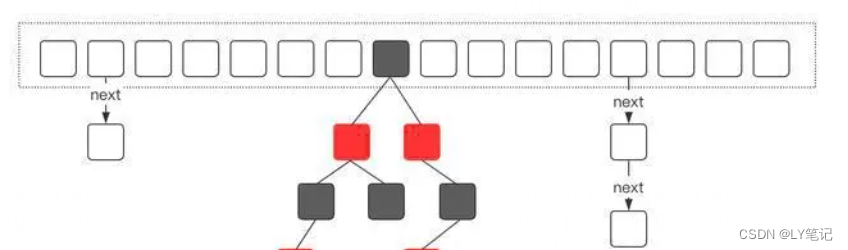
Morris 遍历的是指就是避免用栈结构,而是让下层到上层有指针,具体时通过让底层节点指向 null 的空闲指针指回上层的某个节点,从而完成下层到上层的移动。
Morris 遍历的过程:
假设当前节点为cur,初始时cur就是整棵树的头节点,根据以下标准让cur移动:
1. 如果 cur 为 null,则过程停止,否则继续下面的过程。
2. 如果 cur 没有左子树,则让cur向右移动,即令 cur = cur.right。
3. 如果 cur 有左子树,则找到cur左子树上最右的节点,记为 mostRight。
1)如果 mostRight 的right指针指向null,则令 mostRight.right = cur,也就是让mostRight 的right指针指向当前节点,然后让cur向左移动,即令 cur = cur.left。
2)如果 mostRight 的right指针指向cur,则令 mostRight.right = null,也就是让 mostRight的right指针指向null,然后让cur向右移动,即令cur = cur.right。
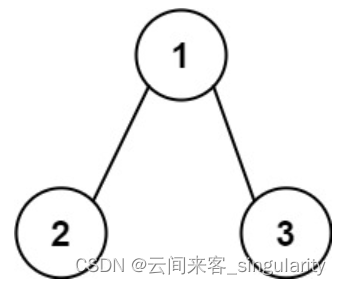
举例:
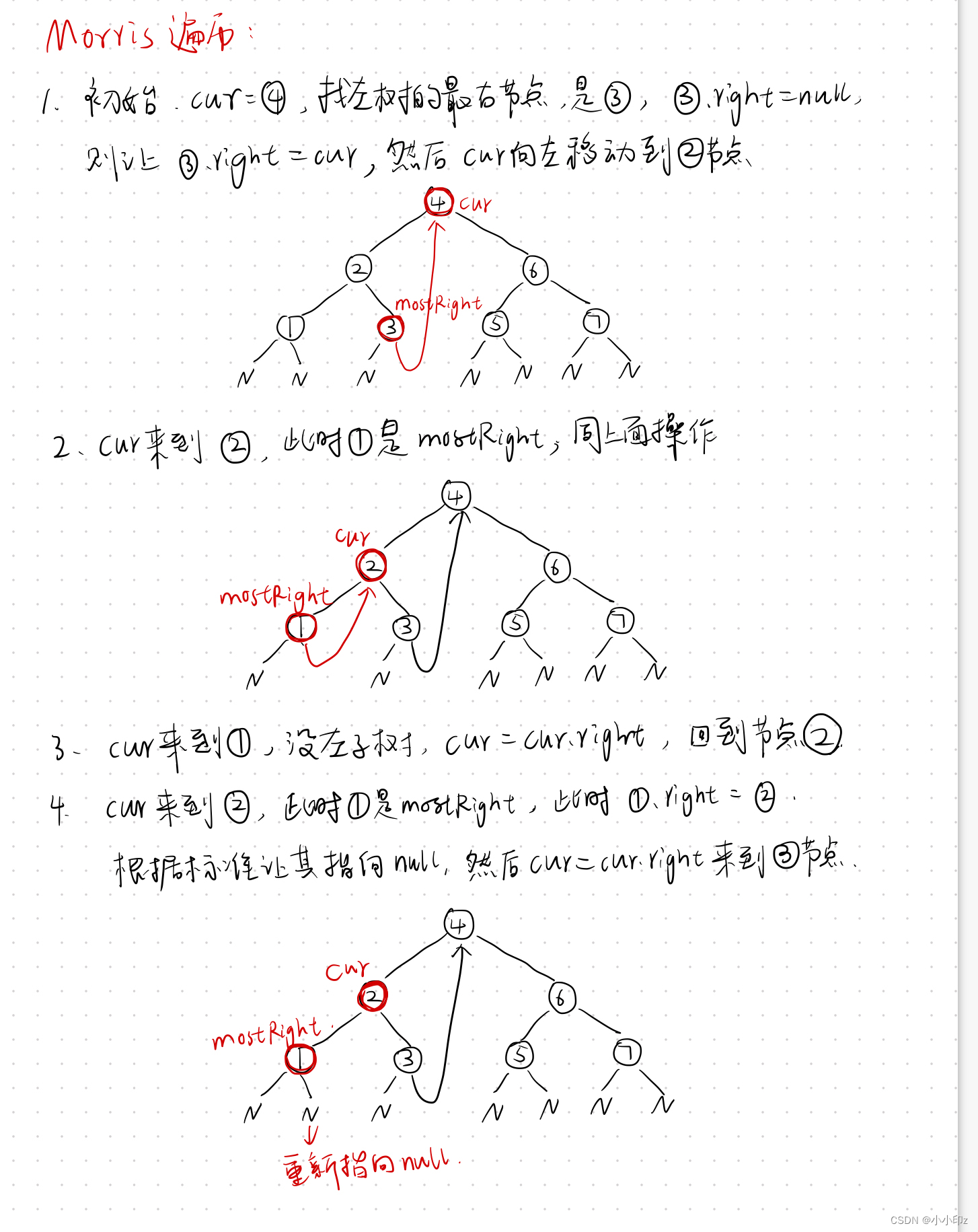
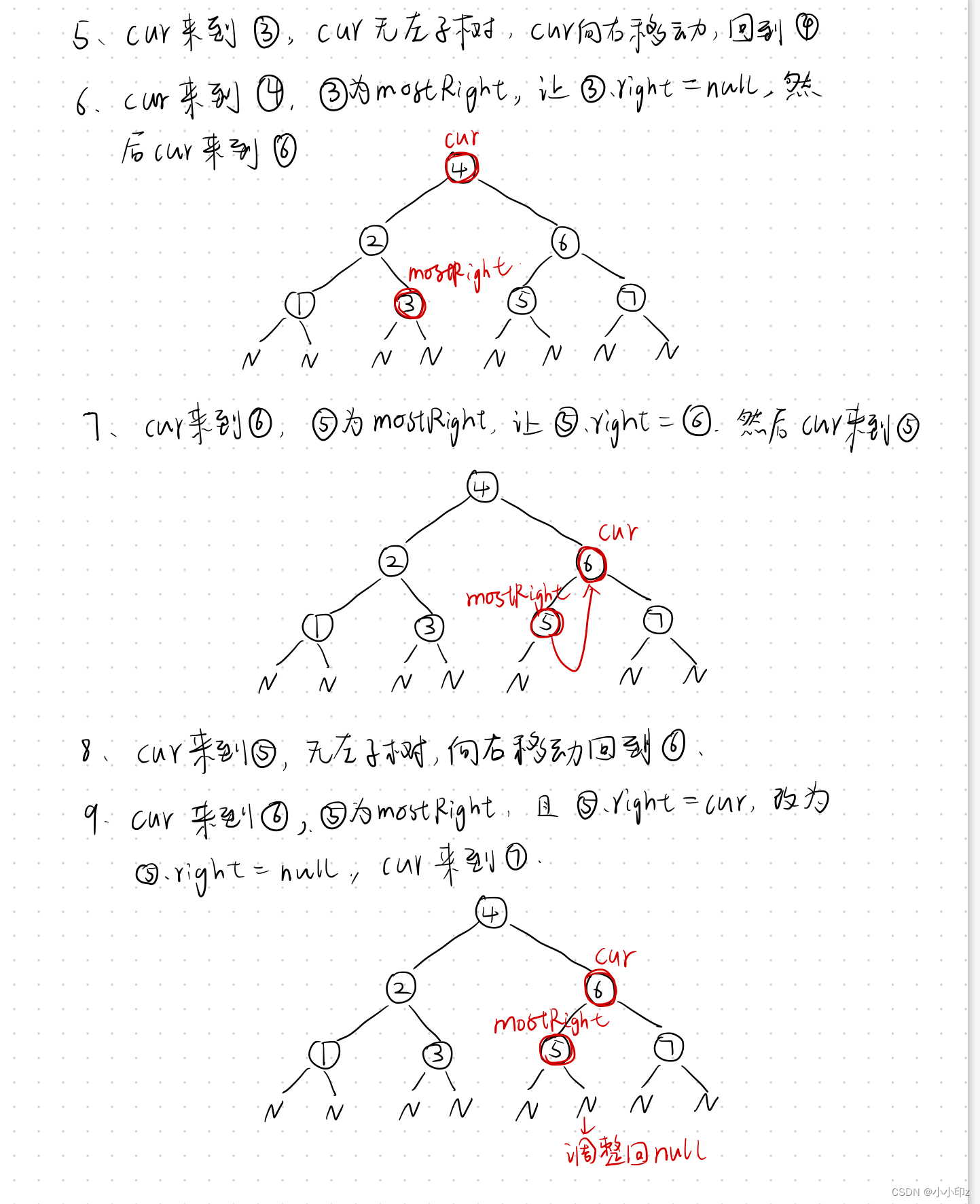

Morris 序代码实现:
public static void morris(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
//如果当前cur有左子树
if (mostRight != null) {
//找到左子树上最右的节点
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
//上面的while结束后,mostRight就是最右的节点
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;//回到最外层的while,继续判断cur的情况
} else {
//如果mostRight指向cur 让其指回null
mostRight.right = null;
}
}
//cur如果没有左子树,cur向右移动
//或者cur左子树的最右节点的右指针是指向cur的,cur向右移动
cur = cur.right;
}
}根据 Morris 遍历,加工出先序遍历:
1. 对于cur只能到达一次的节点(无左子树的节点),cur到达时直接打印
2. 对于cur可以到达两次的节点(有左子树的节点),cur第一次到达时打印,第二次到达时不打印。
先序遍历:
public static void morrisPre(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
//这里是有左子树的情况
if (mostRight != null) {
//这个while循环就是找 mostRight节点
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
//当mostRight 为空时,说明第一次到达这个节点 直接打印。
if (mostRight.right == null) {
mostRight.right = cur;
System.out.print(cur.value + " ");
cur = cur.left;
continue;
//这里说明第二次到达这个节点 在先序中不在此处打印
} else {
mostRight.right = null;
}
//这里就是没有左子树的情况 直接打印
} else {
System.out.print(cur.value + " ");
}
cur = cur.right;
}
}根据 Morris 遍历,加工出中序遍历:
1. 对于cur只能到达一次的节点(无左子树的节点),cur到达时直接打印
2. 对于cur可以到达两次的节点(有左子树的节点),cur第一次到达时不打印,第二次到达时打印。
中序遍历:
public static void morrisIn(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
//这里是有左子树的情况
if (mostRight != null) {
//这个while循环就是找 mostRight节点
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
//当mostRight 为空时,说明第一次到达这个节点 中序中不打印。
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
//这里说明第二次到达这个节点 在中序中此处需要打印
} else {
System.out.print(cur.value + " ");
mostRight.right = null;
}
//这里就是没有左子树的情况 直接打印
} else {
System.out.print(cur.value + " ");
}
cur = cur.right;
}
}测试结果:
Node head = new Node(1);
Node node1 = new Node(2);
Node node2 = new Node(3);
Node node3 = new Node(4);
Node node4 = new Node(5);
Node node5 = new Node(6);
head.left = node1;
head.right = node2;
node1.left = node3;
node1.right = node4;
node2.right = node5;
morrisPre(head);
System.out.println();
morrisIn(head);