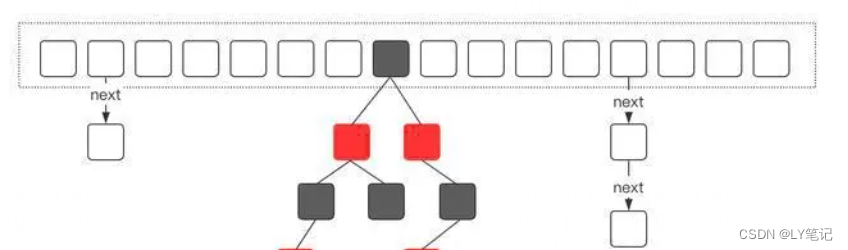
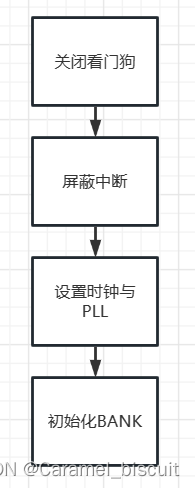
众所周知，深度神经网络（DNN）容易受到对抗性攻击，这种攻击是通过在良性示例中添加精心设计的扰动来实现的。基于最小-最大鲁棒优化的对抗性训练可以提供对抗性攻击的安全概念。然而，对抗性鲁棒性需要比仅具有良性示例的自然训练更大的网络容量。本文提出了一种并行对抗性训练和权重修剪的框架，该框架在保持对抗性鲁棒性的同时实现了模型压缩，并从本质上解决了对抗性训练的困境。此外，本工作研究了传统环境中关于权重修剪的两个假设，并发现在对抗环境中，权重修剪对于减小网络模型大小至关重要；即使从大模型继承了初始化，从头开始训练小模型也不能实现对抗性鲁棒性和高标准精度。

我们构建了一个框架，通过实现并行权重修剪和对抗性训练，实现对抗性鲁棒性和模型压缩。具体而言，由于其与对抗性训练的兼容性，我们在我们的框架中使用基于ADMM（交替方向乘数法）的修剪[50，51]。更重要的是，基于ADMM的修剪是通用的，因为它支持不规则修剪和不同类型的规则修剪，这样我们可以轻松地在不同的修剪方案之间进行切换，以进行公平比较。最终，我们的框架解决了对抗性训练的困境。

我们还研究了针对传统模型压缩设置提出的两个关于权重修剪的假设，并通过实验验证了它们对于对抗性训练设置的有效性。我们发现，权重修剪对于减少对抗性环境中的网络模型大小至关重要，即使从大模型继承初始化，从头开始训练小模型也无法同时实现对抗性鲁棒性和高标准精度。

利用所提出的并行对抗训练和权重剪枝框架，我们系统地研究了不同剪枝方案对对抗鲁棒性和模型压缩的影响。我们发现，在修剪DNN模型时，不规则修剪方案最能保持标准精度和对抗性鲁棒性

Concurrent Adversarial Training and Weight Pruning

在本节中，我们提供了并行对抗性训练和权重修剪的框架。我们以一种适用于ADMM（交替方向乘数法）的方式来表述问题：

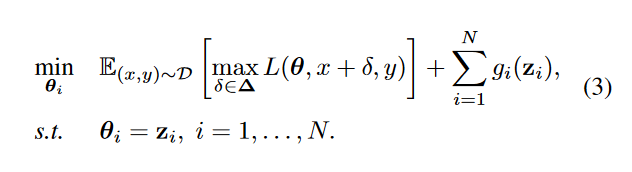
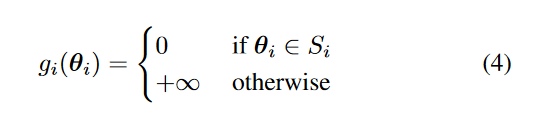
是结合权重稀疏性约束的指示符函数（可以通过集合Si定义不同的权重修剪方案）。zi是启用基于ADMM的解决方案的辅助变量

通过形成增广拉格朗日量，ADMM框架将问题（3）分解为迭代求解的两个子问题：

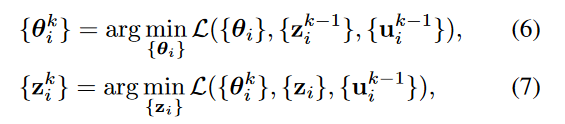
拉格朗日乘数更新为：

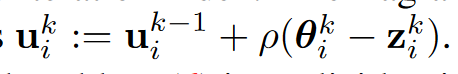
等式6可以被解决为：

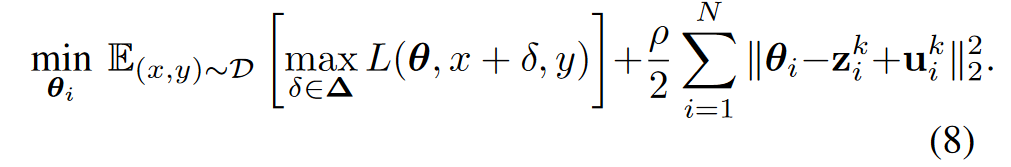
（8）的目标函数中的第一项是最小-最大问题。与解决对抗性训练问题相同，这里我们可以使用具有T次迭代和随机启动的PGD攻击来解决内部最大化问题。在一个普遍的第一级对手面前，内部问题是可以解决的。（8）中的第二凸二次项由于（5）中的增广项的存在而出现。给定对抗性扰动δ，我们可以应用随机梯度下降算法来解决总体最小化问题。由于损失函数的非凸性，不能保证解的全局最优性。然而，当适当选择ρ时，ADMM可以提供局部最优解，因为当ρ>0时，（8）中的二次项是强凸的，这稳定了ADMM的收敛。

等式7可以被解决为：

注意，gi（·）是Si定义的指标函数，因此可以解析和优化地解决此子问题[5]。最佳解决方案是

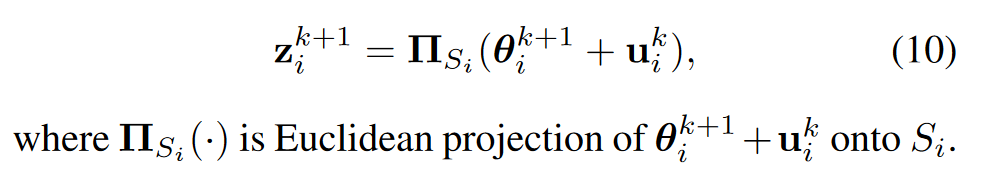
Definitions of Si for Weight Pruning Schemes

Filter pruning

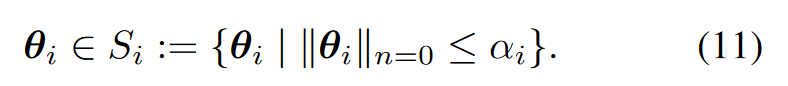
Column pruning

Irregular pruning

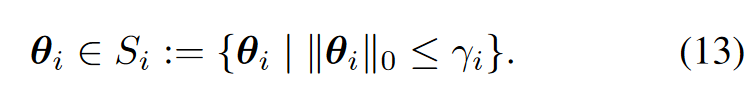
算法