策略迭代算法

通过策略评估与策略提升不断循环交替，得到最优策略。

策略评估

固定策略 $\pi$ 不变，估计状态价值函数V

一个策略的状态价值函数，在马尔可夫决策过程中提到过：
$$V^{\pi }(s)=\sum _{a\in A}\pi (a|s)\left(r(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)V^{\pi }(s^{\prime })\right)$$
$\pi (a|s)$ 是在状态 $s$ 下采取动作 $a$ 的概率。在知道奖励函数和状态转移函数后，可以用下一个状态的价值来计算当前状态的价值，更一般的，考虑所有的状态，就变成了用上一轮的状态价值函数来计算当前这一轮的状态价值函数。
$$V^{k+1}(s)=\sum _{a\in A}\pi (a|s)\left(r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^k(s^{\prime })\right)$$
可以选取初始值 $V^0$ ，当 $V^k=V^{\pi }$ 时，停止更新，若 $k\to \infty$ ，$V^k$ 会收敛到 $V^{\pi }$ ，若 ${\max }_{s\in \mathcal{S}}|V^{k+1}(s)-V^k(s)|$ 非常小，则也可以认为完成收敛。

策略提升

根据估计好的状态价值函数V结合策略推算出动作价值函数Q，并对 Q 函数优化然后进一步改进策略

假设确定存在一个确定性策略 ${\pi }^{\prime }$ ，在任意一个状态下，都满足：
$$Q^{\pi }(s,{\pi }^{\prime }(s))\ge V^{\pi }(s)$$
$$\begin{array}{rl}{V}^{\pi }(s)& \le Q^{\pi }(s,{\pi }^{\prime }(s))\\ & ={\mathbb{E}}_{{\pi }^{\prime }}[R_t+\gamma V^{\pi }(S_{t+1})|S_t=s]\\ & \le {\mathbb{E}}_{{\pi }^{\prime }}[R_t+\gamma Q^{\pi }(S_{t+1},{\pi }^{\prime }(S_{t+1}))|S_t=s]\\ & ={\mathbb{E}}_{{\pi }^{\prime }}[R_t+\gamma R_{t+1}+{\gamma }^2{V}^{\pi }(S_{t+2})|S_t=s]\\ & \le {\mathbb{E}}_{{\pi }^{\prime }}[R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{V}^{\pi }(S_{t+3})|S_t=s]\\ & \le {\mathbb{E}}_{{\pi }^{\prime }}[R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+\cdots |S_t=s]\\ & =V^{{\pi }^{\prime }}(s)\end{array}$$
通过选取动作从而得到新的策略的过程称为策略提升，当 ${\pi }^{\prime }$ 与 $\pi$ 一样好时，可以证明策略迭代达到了收敛：
π ′ ( s ) = arg ⁡ max ⁡ a Q π ( s , a ) = arg ⁡ max ⁡ a { r ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) } \pi'(s)=\arg\max_aQ^\pi(s,a)=\arg\max_a\{r(s,a)+\gamma\sum_{s'}P(s'|s,a)V^\pi(s')\} π′(s)=argamax​Qπ(s,a)=argamax​{r(s,a)+γs′∑​P(s′∣s,a)Vπ(s′)}

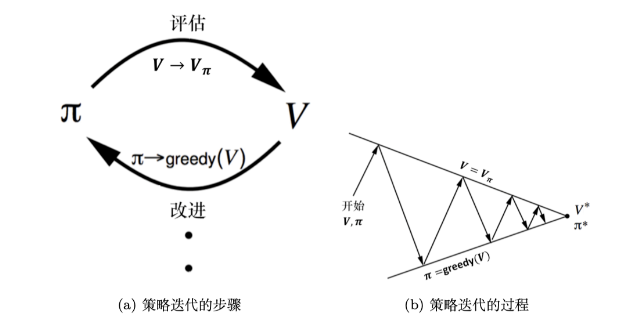
策略迭代算法的实现

• 随机初始化策略$\pi (s)$与价值函数$V(s)$
• while $\Delta >\theta$ do:（状态评估）
  • $\Delta \leftarrow 0$
  • 对于每个状态$s\in S$ :
    • $v\leftarrow V(S)$
    • $V(s)\leftarrow r(s,\pi (s))+\gamma {\sum }_{s^{\prime }}P(s^{\prime }|s,\pi (s))V(s^{\prime })$
    • $\Delta \leftarrow max(\Delta ,|v\ast V(s)|)$
• end while
• ${\pi }_{old}\leftarrow \pi$
• 对于每个状态$s\in S$:
  • $\pi (s)\leftarrow \arg {\max }_{a}r(s,a)+\gamma {\sum }_{s^{\prime }}P(s^{\prime }|s,a)V(s^{\prime })$
• 如果${\pi }_{old}=\pi$，则停止算法并返回V和$\pi$ ,否则转到策略评估循环

class PolicyIteration:
    def __init__(self,env,theta,gamma):
        self.env=env
        # 初始化价值为0
        self.v=[0]*self.env.ncol*self.env.nrow
        # 初始化为均匀随机策略
        self.pi=[[0.25,0.25,0.25,0.25] for i in range(self.env.ncol*self.env.nrow)]
        self.theta=theta # 策略评估收敛阈值
        self.gamma=gamma # 折扣因子
    
    # 策略评估
    def policyEvaluation(self):
        cnt =1 #计数
        while 1:
            maxDiff=0
            newV=[0] * self.env.ncol * self.env.nrow
            for s in range(self.env.ncol*self.env.nrow):
                #计算每一个状态s下所有Q(s,a)之和的价值
                qsaList=[]
                # 有四个动作
                for a in range(4):
                    qsa=0
                    for transition in self.env.P[s][a]:
                        p,nextState,r,done=transition
                        qsa+=p*(r+self.gamma*self.v[nextState]*(1-done))
                    # 策略*Q（s,a）=对应的价值
                    # 本章环境比较特殊,奖励和下一个状态有关,所以需要和状态转移概率相乘
                    qsaList.append(self.pi[s][a]*qsa)
                # 求和后得到状态s的状态价值
                newV[s]=sum(qsaList)
                maxDiff=max(maxDiff,abs(newV[s]-self.v[s]))
            self.v=newV
            #满足收敛条件，退出评估迭代
            if maxDiff<self.theta:
                break
            cnt +=1
        print(f'policyEvaluation 次数为{cnt}')

    def policyImprovement(self):
        # 策略提升
        for s in range(self.env.ncol*self.env.nrow):
            qsaList=[]
            for a in range(4):
                qsa=0
                for transition in self.env.P[s][a]:
                    p,nextState,r,done=transition
                    qsa+=p*(r+self.gamma*self.v[nextState]*(1-done))
                # 策略*Q（s,a）=对应的价值
                qsaList.append(qsa)
            maxq=max(qsaList)
            cntq=qsaList.count(maxq)# 计算有几个动作得到了最大的Q值
            self.pi[s]=[1/cntq if q==maxq else 0 for q in qsaList]
        print('policyImprovement')
        return self.pi
    
    def policyIteration(self):   
        # 策略迭代
        while 1:
            self.policyEvaluation()
            oldPi=copy.deepcopy(self.pi)
            newPi=self.policyImprovement()
            if oldPi==newPi:
                break   

为了更好地展现最终的策略，接下来增加一个打印策略的函数，用于打印当前策略在每个状态下的价值以及智能体会采取的动作。对于打印出来的动作，我们用^o<o表示等概率采取向左和向上两种动作，ooo>表示在当前状态只采取向右动作。

def print_agent(agent, action_meaning, disaster=[], end=[]):
    print("状态价值：")
    for i in range(agent.env.nrow):
        for j in range(agent.env.ncol):
            # 为了输出美观,保持输出6个字符
            print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')
        print()

    print("策略：")
    for i in range(agent.env.nrow):
        for j in range(agent.env.ncol):
            # 一些特殊的状态,例如悬崖漫步中的悬崖
            if (i * agent.env.ncol + j) in disaster:
                print('****', end=' ')
            elif (i * agent.env.ncol + j) in end:  # 目标状态
                print('EEEE', end=' ')
            else:
                a = agent.pi[i * agent.env.ncol + j]
                pi_str = ''
                for k in range(len(action_meaning)):
                    pi_str += action_meaning[k] if a[k] > 0 else 'o'
                print(pi_str, end=' ')
        print()


env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001
gamma = 0.9
agent = PolicyIteration(env, theta, gamma)
agent.policy_iteration()
print_agent(agent, action_meaning, list(range(37, 47)), [47])

策略评估进行51轮后完成
policyImprovement
策略评估进行78轮后完成
policyImprovement
策略评估进行39轮后完成
policyImprovement
策略评估进行11轮后完成
policyImprovement
策略评估进行1轮后完成
policyImprovement
状态价值：
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000  0.000
策略：
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo ^v<> ^v<> ^v<> ^v<> ^v<> ^v<> ^v<> ^v<> ^v<> ^v<> ^v<>