SpikingJelly笔记之泊松编码

news2024/9/21 4:32:50

文章目录

前言
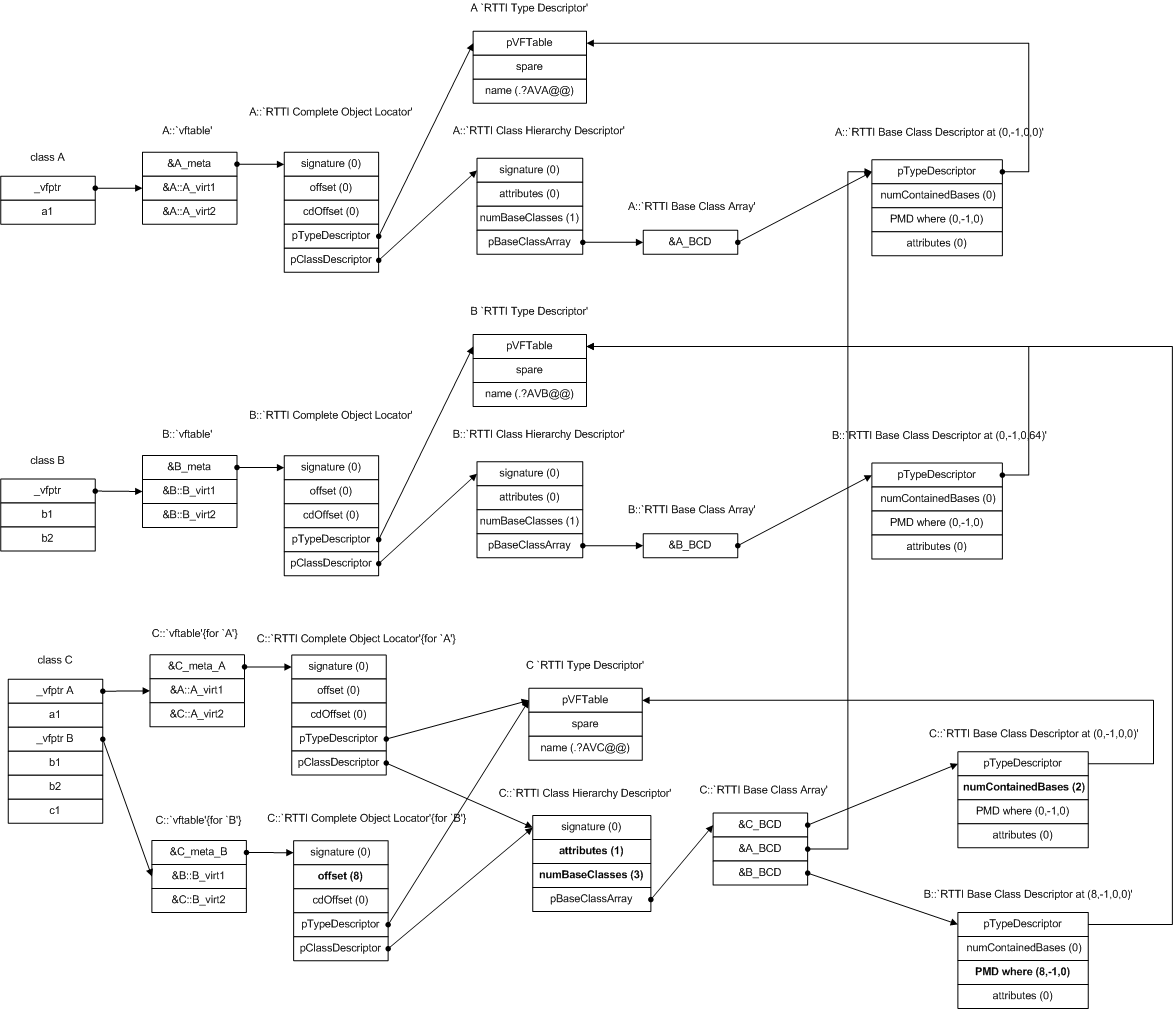
一、泊松编码的原理
二、生成符合泊松分布的脉冲序列
三、SpikingJelly中的泊松编码
四、Lena图像的泊松编码与还原
- 1.原始图像
- 2.图像编码
- 3.图像还原
总结

前言

记录SpikingJelly中泊松编码的使用方法，对图像数据进行编码与还原

一、泊松编码的原理

基于频率的编码方式，将输入编码为发放次数分布符合泊松过程的脉冲序列
$P(X=k)=\frac{{\lambda}^{k}}{k!}{e}^{-\lambda}$
均值λ：时间T内发放的脉冲数目
根据输入决定每个时间步发放脉冲的概率[0,1]，各时间步相互独立

二、生成符合泊松分布的脉冲序列

out_spike = torch.rand_like(x).le(x).to(x)

（1）生成与输入形状相同的标准正态分布随机值
（2）将生成值与输入[0,1]比较，<=为1，>为0
（3）将比较生成的布尔值转化为与输入相同的数据类型

三、SpikingJelly中的泊松编码

from spikingjelly.activation_based import encoding
pe = encoding.PoissonEncoder() # 泊松编码器
# 输出脉冲序列，T：时间步长，w：图像宽度，h：图像高度
out_spike = torch.zeros((T, w, h), dtype=torch.bool)
# 按时间步根据输入生成脉冲序列，相互独立
for t in range(T):
    out_spike[t] = pe(x) # x需要归一化[0,1]

四、Lena图像的泊松编码与还原

1.原始图像

读取、展示原始图像

####################泊松编码####################
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
import torch
from spikingjelly.activation_based import encoding
from spikingjelly import visualizing
####################读取图像####################
img = np.array(Image.open('../dataset/lena.bmp')) / 255
x = torch.from_numpy(img)
w, h = x.shape
plt.figure()
plt.imshow(x, cmap='gray')
plt.axis('off')

2.图像编码

输出泊松编码后每个时间步的图像

####################泊松编码####################
T = 9 # 时间步长
pe = encoding.PoissonEncoder()
out_spike = torch.zeros((T, w, h), dtype=torch.bool)
for t in range(T):
    out_spike[t] = pe(x)
# 每个时间步的编码图像
nrows, ncols, space = 3, 3, 30
figsize, dpi = (6, 4), 200
visualizing.plot_2d_feature_map(x3d=out_spike.float().numpy(),
                                nrows=nrows,
                                ncols=ncols,
                                space=space,
                                title='PoissonEncoder',
                                figsize=figsize,
                                dpi=dpi)

3.图像还原

按时间步累加可重构出原始图像，时间步T越长，累加结果越接近原始图像

####################编码结果累加####################
T = 100 # 时间步长
pe = encoding.PoissonEncoder()
out_spike = torch.zeros((w, h), dtype=torch.float)
out_spikes = torch.zeros((5, w, h), dtype=torch.float)
# 按时间步累加
show_step = 20
for t in range(T):
    out_spike += pe(x)
    if(t % show_step == 0):
        out_spikes[t//show_step] = out_spike
# 归一化
for i in range(T//show_step):
    out_spikes[i] = (out_spikes[i]-out_spikes[i].min()) / (out_spikes[i].max()-out_spikes[i].min())
# 按时间步累加的编码图像
nrows, ncols, space = 1, T//show_step, 30
figsize, dpi = (6, 4), 200
visualizing.plot_2d_feature_map(x3d=out_spikes.numpy(),
                                nrows=nrows,
                                ncols=ncols,
                                space=space,
                                title='PoissonEncoder',
                                figsize=figsize,
                                dpi=dpi)
plt.axis('off')
plt.show()