文章目录
- Roadmap
- 🟡基础概念
- 贝尔曼方程(Bellman Equation)
- 基本形式
- 矩阵-向量形式
- 迭代求解
- 状态值 vs. 动作值
- 🟡贝尔曼最优方程(Bellman Optimality Equation,BOE)
- 基本形式
- 迭代求解
本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程(参考资料1),并参考了部分参考资料2、3的内容进行补充。
系列博文索引:
- 强化学习的数学原理学习笔记 - RL基础知识
- 强化学习的数学原理学习笔记 - 基于模型(Model-based)
- 强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
- 强化学习的数学原理学习笔记 - 时序差分学习(Temporal Difference)
- 强化学习的数学原理学习笔记 - 值函数近似(Value Function Approximation)
- 强化学习的数学原理学习笔记 - 策略梯度(Policy Gradient)
- 强化学习的数学原理学习笔记 - Actor-Critic
参考资料:
- 【强化学习的数学原理】课程:从零开始到透彻理解(完结)(主要)
- Sutton & Barto Book: Reinforcement Learning: An Introduction
- 机器学习笔记
*注:【】内文字为个人想法,不一定准确
Roadmap
*图源:https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning
🟡基础概念
MDP概念:
- 状态(state)、动作(action)、奖励(reward)
- 状态转移概率: p ( s ′ ∣ s , a ) p(s'|s, a) p(s′∣s,a)
- 奖励概率: p ( r ∣ s , a ) p(r|s, a) p(r∣s,a)
马尔可夫性质:与历史无关(memoryless)
其他概念:轨迹(trajectory)、episode / trail、确定性(deterministic)、随机性(stochastic)
| 名称 | 含义 | 形式 | 备注 |
|---|---|---|---|
| 策略(policy) | 从状态映射至所有动作的概率分布 | π ( a ∣ s ) \pi(a | s) π(a∣s):在状态 s s s下选择动作 a a a的概率 | 策略决定了每个状态下应该执行什么样的动作 |
| 期望折扣回报(expected discounted return) | 略 *reward和return的区别:reward指单步的奖励,return指多步的折扣回报 |
G
t
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
⋯
=
∑
t
=
0
∞
γ
t
R
t
+
k
+
1
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{t=0}^{\infty} \gamma^t R_{t+k+1}
Gt=Rt+1+γRt+2+γ2Rt+3+⋯=∑t=0∞γtRt+k+1 - γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]:折扣因子 - 习惯性写成 R t + 1 R_{t+1} Rt+1,而非 R t R_t Rt | 评估某个策略的好坏,针对单个trajectory |
| 值函数 / 状态值函数(state-value function) | 从状态 s s s开始遵循策略 π \pi π取得的预期总回报(均值) | v π ( s ) = E π [ G t ∣ S t = s ] v_{\pi}(s) = \mathbb{E}_\pi [ G_t | S_t = s ] vπ(s)=Eπ[Gt∣St=s]:策略 π \pi π的状态-值函数 | 评估某个状态本身的价值,进而反映对应策略的价值 |
| Q函数 / 动作值函数(action-value function) | 从状态 s s s开始采取动作 a a a,之后遵循策略 π \pi π取得的预期总回报(均值) | q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] q_{\pi}(s, a) = \mathbb{E}_\pi [ G_t | S_t = s, A_t = a ] qπ(s,a)=Eπ[Gt∣St=s,At=a]:策略 π \pi π的动作-值函数 | 评估某个状态下特定动作的价值,注意动作 a a a可以不遵循策略 π \pi π |
贝尔曼方程(Bellman Equation)
基本形式
每个状态
S
t
S_t
St的值函数,实际上等于按照策略
π
\pi
π行动后的奖励(
R
t
+
1
R_{t+1}
Rt+1)加上后一个状态
S
t
+
1
S_{t+1}
St+1的值函数的折扣值(
γ
G
t
+
1
\gamma G_{t+1}
γGt+1),也就是即时奖励(immediate reward)和未来奖励(future rewards)的和。这种思想叫做Bootstrapping(自举法),对应的公式就是贝尔曼方程:
v
π
(
s
)
=
E
[
R
t
+
1
+
γ
G
t
+
1
∣
S
t
=
s
]
=
∑
a
π
(
a
∣
s
)
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
π
(
s
′
)
]
,
∀
s
∈
S
\begin{aligned} v_\pi(s) &= \mathbb{E}[R_{t+1} + \gamma G_{t+1} | S_t =s] \\ &= \sum_a \pi (a|s) \sum_{s', r} p(s', r|s, a) [r + \gamma v_\pi(s')], \quad \forall s\in \mathcal {S} \end{aligned}
vπ(s)=E[Rt+1+γGt+1∣St=s]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)],∀s∈S
贝尔曼方程描述了不同状态之间的值函数的关系。给定策略后求解贝尔曼方程的过程 也称之为策略评估(Policy Evaluation)。
比如有两个策略
π
1
\pi_1
π1和
π
2
\pi_2
π2,如果对于任何
s
∈
S
s\in \mathcal {S}
s∈S,
v
π
1
(
s
)
≥
v
π
2
(
s
)
v_{\pi_1} (s) \geq v_{\pi_2} (s)
vπ1(s)≥vπ2(s)都成立,那么可以认为
π
1
\pi_1
π1优于
π
2
\pi_2
π2。
矩阵-向量形式
贝尔曼方程也可以转化为矩阵-向量形式:
v
π
=
r
π
+
γ
P
π
v
π
v_\pi = r_\pi + \gamma P_\pi v_\pi
vπ=rπ+γPπvπ
- 状态向量: v π = [ v π ( s 1 ) , ⋯ , v π ( s n ) ] T ∈ R n v_\pi = [v_\pi(s_1), \cdots, v_\pi(s_n)]^T \in \mathbb{R}^n vπ=[vπ(s1),⋯,vπ(sn)]T∈Rn
- 奖励向量: r π = [ r π ( s 1 ) , ⋯ , r π ( s n ) ] T ∈ R n r_\pi = [r_\pi(s_1), \cdots, r_\pi(s_n)]^T \in \mathbb{R}^n rπ=[rπ(s1),⋯,rπ(sn)]T∈Rn
- 状态转移矩阵: P π ∈ R n × n P_\pi \in \mathbb{R}^{n\times n} Pπ∈Rn×n,其中 [ P π ] i j = p π ( s j ∣ s i ) [P_\pi]_{ij} = p_\pi (s_j|s_i) [Pπ]ij=pπ(sj∣si)
*四个状态时的示例:
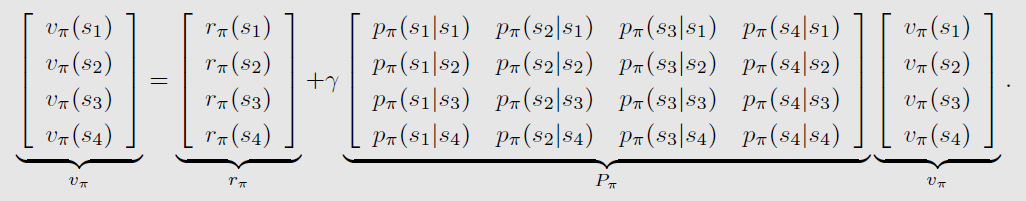
迭代求解
v
k
+
1
=
r
π
+
γ
P
π
v
k
v_{k+1} = r_\pi + \gamma P_\pi v_k
vk+1=rπ+γPπvk
先假设一个
v
k
v_k
vk的值,基于该值计算出
v
k
+
1
v_{k+1}
vk+1,进而重复该过程不断计算出
v
k
+
2
,
v
k
+
3
,
⋯
v_{k+2}, v_{k+3}, \cdots
vk+2,vk+3,⋯。
可以证明,当
k
→
∞
k \rarr \infin
k→∞时,
v
k
v_k
vk会收敛到
v
π
v_\pi
vπ。
状态值 vs. 动作值
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_\pi (s) = \sum_a \pi (a | s) q_\pi (s, a)
vπ(s)=∑aπ(a∣s)qπ(s,a)
状态值可以看作是策略
π
\pi
π的每个动作值的加权平均。
q
π
(
s
,
a
)
=
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
π
(
s
′
)
]
q_\pi (s,a) = \sum_{s', r} p(s', r|s, a) [r + \gamma v_\pi(s')]
qπ(s,a)=∑s′,rp(s′,r∣s,a)[r+γvπ(s′)]
动作值可以通过状态值求解,也可以不依赖于状态值求解。
🟡贝尔曼最优方程(Bellman Optimality Equation,BOE)
RL的目标是最大化累计奖励,则必然存在至少一个最优策略,记作 π ∗ \pi_* π∗,其对任意策略 π \pi π都满足: v π ∗ ( s ) ≥ v π ( s ) , ∀ s ∈ S v_{\pi_*} (s) \geq v_{\pi}(s), \forall s\in \mathcal{S} vπ∗(s)≥vπ(s),∀s∈S。
基本形式
最优策略共享相同的最优状态值
v
∗
v_*
v∗与最优动作值
a
∗
a_*
a∗。寻找最优策略相当于求贝尔曼方程(
v
π
v_\pi
vπ、
a
π
a_\pi
aπ)的最优解(
max
π
\max_\pi
maxπ),则贝尔曼最优方程为:
v
∗
(
s
)
=
max
π
v
π
(
s
)
=
max
π
∑
a
π
(
a
∣
s
)
q
π
(
s
,
a
)
\begin{aligned} v_*(s) &= \max_{\pi} v_{\pi}(s) \\ &= \max_{\pi} \sum_a \pi (a | s) q_\pi (s, a) \end{aligned}
v∗(s)=πmaxvπ(s)=πmaxa∑π(a∣s)qπ(s,a)
q
∗
(
s
,
a
)
=
max
π
q
π
(
s
,
a
)
=
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
∗
(
s
′
)
]
\begin{aligned} q_*(s, a) &= \max_{\pi} q_{\pi}(s, a) \\ &= \sum_{s',r} p(s', r|s, a) [r + \gamma v_* (s')] \end{aligned}
q∗(s,a)=πmaxqπ(s,a)=s′,r∑p(s′,r∣s,a)[r+γv∗(s′)]
对应的矩阵-向量形式:
v
=
max
π
(
r
π
+
γ
P
π
v
)
v = \max_\pi (r_\pi+\gamma P_\pi v)
v=maxπ(rπ+γPπv)
贝尔曼最优方程是一个特殊的贝尔曼方程,即当策略
π
\pi
π为最优策略
π
∗
\pi_*
π∗时的贝尔曼方程:
π
∗
=
arg max
π
(
r
π
+
γ
P
π
v
∗
)
\pi_* = \argmax_\pi (r_\pi + \gamma P_\pi v_*)
π∗=argmaxπ(rπ+γPπv∗)
v
∗
=
(
r
π
∗
+
γ
P
π
∗
v
∗
)
v_* = (r_{\pi_*}+\gamma P_{\pi_*} v_*)
v∗=(rπ∗+γPπ∗v∗)
注意:
- 最优状态值唯一,但最优策略并不唯一
- 对于一个给定系统,其最优状态值和最优策略受奖励值
r
r
r与折扣因子
γ
\gamma
γ的影响
- 最优策略不受奖励值的绝对大小影响,但受其相对大小影响
- 折扣因子越小(接近0),策略越短视,反之(接近1)策略越长远
迭代求解
考虑贝尔曼最优方程的矩阵-向量形式,设 f ( v ) = max π ( r π + γ P π v ) f(v) = \max_\pi (r_\pi+\gamma P_\pi v) f(v)=maxπ(rπ+γPπv),则贝尔曼最优方程可以写作: v = f ( v ) v = f(v) v=f(v)。
- 其中 f ( v ) f(v) f(v)为向量, [ f ( v ) ] s = max π ∑ a π ( a ∣ s ) q ( s , a ) , ∀ s ∈ S [f(v)]_s = \max_\pi \sum_a \pi(a|s)q(s, a), \quad\forall s\in\mathcal{S} [f(v)]s=maxπ∑aπ(a∣s)q(s,a),∀s∈S
基于压缩映射定理(contraction mapping theorem)可知,
v
=
f
(
v
)
v = f(v)
v=f(v)的解(即最优状态值
v
∗
v_*
v∗)存在且唯一。可以通过迭代的方式进行求解,即:
v
k
+
1
=
max
π
(
r
π
+
γ
P
π
v
k
)
v_{k+1} = \max_\pi (r_\pi+\gamma P_\pi v_k)
vk+1=maxπ(rπ+γPπvk),其中
k
=
0
,
1
,
2
,
⋯
k=0, 1,2,\cdots
k=0,1,2,⋯
可以证明,当
k
→
∞
k\rarr \infin
k→∞时,
v
k
→
v
∗
v_k\rarr v_*
vk→v∗。
通常的求解流程:【实际上就是基于模型(Model-based)中的值迭代(Value Iteration)算法】
- 对于任意一个状态 s ∈ S s\in\mathcal{S} s∈S,估计当前的状态值为 v k ( s ) v_k(s) vk(s)
- 对于任意一个动作
a
∈
A
(
s
)
a\in\mathcal{A}(s)
a∈A(s),计算
q
k
(
s
,
a
)
=
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
k
(
s
′
)
]
q_k(s,a) = \sum_{s',r} p(s', r|s, a) [r + \gamma v_k (s')]
qk(s,a)=∑s′,rp(s′,r∣s,a)[r+γvk(s′)]
- v k ( s ′ ) v_k (s') vk(s′)在第一次迭代时取初始值,后续迭代时使用前一轮迭代中更新后的值
- 计算状态s下的确定性贪婪策略
π
k
+
1
(
a
∣
s
)
=
{
1
a
=
a
k
∗
(
s
)
0
a
≠
a
k
∗
(
s
)
\pi_{k+1}(a|s) = \begin{cases} 1 &a = a_k^*(s) \\ 0 &a \neq a_k^*(s) \end{cases}
πk+1(a∣s)={10a=ak∗(s)a=ak∗(s)
- a k ∗ ( s ) = arg max a q k ( s , a ) a_k^*(s) = \argmax_a q_k(s, a) ak∗(s)=argmaxaqk(s,a),表示使得当前状态动作值最大的那个动作
- 计算
v
k
+
1
(
s
)
=
max
a
q
k
(
s
,
a
)
v_{k+1}(s) = \max_a q_k (s, a)
vk+1(s)=maxaqk(s,a),继续下一轮迭代
- v k + 1 ( s ) v_{k+1}(s) vk+1(s)实际上就是上一步的最优动作对应的动作值(因为当前策略下其他动作的概率均为0)
在实际应用中,当 ∥ v k + 1 ( s ) − v k ( s ) ∥ \|v_{k+1}(s) -v_{k}(s)\| ∥vk+1(s)−vk(s)∥低于某个阈值(如0.001)之后,就可以认为算法收敛了。
由于精确求解贝尔曼方程往往需要极高的计算开销,所以通常只获得近似解即可。
压缩映射定理(contraction mapping theorem),又称巴拿赫不动点定理(Banach fixed-point theorem)
参考:
- 非常神奇的数学结论有哪些? - 知乎
- Chapter 3: The Contraction Mapping Theorem - UC Davis Math
- 巴拿赫不动点定理 - 维基百科
直观认识:
将世界地图放在一个桌子上,则该桌子上必有一点,其实际位置会和地图上该点的对应位置重合,该点称之为“不动点(fixed point)”。
将该点的实际位置视作变量 x x x,其在地图上的位置视作函数 f ( x ) f(x) f(x),则 f ( x ) f(x) f(x)可以视作对于 x x x的一种“压缩映射”, f ( x ) = x f(x)=x f(x)=x的解即为不动点。
数学描述:
若 ∥ f ( x 1 ) − f ( x 2 ) ∥ ≤ γ ∥ x 1 − x 2 ∥ \|f(x_1)-f(x_2)\| \leq \gamma\| x_1 - x_2 \| ∥f(x1)−f(x2)∥≤γ∥x1−x2∥(其中 γ ∈ ( 0 , 1 ) \gamma\in (0, 1) γ∈(0,1)),则 f f f为关于 x x x的压缩映射。
- 此处 f ( x ) f(x) f(x)与 x x x均为向量, ∥ ⋅ ∥ \|\cdot\| ∥⋅∥为向量范数(vector norm)
- 例如: f ( x ) = 0.5 x f(x) = 0.5x f(x)=0.5x,取 γ = 0.6 \gamma=0.6 γ=0.6则上式成立。
压缩映射定理是指,若 f f f为压缩映射,则必然存在(exist)一个不动点 x ∗ x^* x∗使得 f ( x ∗ ) = x ∗ f(x^*)=x^* f(x∗)=x∗,且 x ∗ x^* x∗唯一(unique)。
求解算法:迭代式算法
对于迭代序列 x k + 1 = f ( x k ) x_{k+1} = f(x_k) xk+1=f(xk),随着 k → ∞ k\rarr\infin k→∞,该序列指数收敛至 x ∗ x^* x∗。
- 例如:以迭代式算法求 f ( x ) = 0.5 x f(x) = 0.5x f(x)=0.5x的不动点,假设 x 0 = 10 x_0=10 x0=10,则可迭代得到: x 1 = 5 , x 2 = 2.5 , x 3 = 1.25 , ⋯ x_1=5, x_2=2.5, x_3=1.25, \cdots x1=5,x2=2.5,x3=1.25,⋯,最终会逼近于0。