目录

一、题目描述

二、题解

思路分析

具体实现

完整代码

---

一、题目描述

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空） 子数组 的数目。

子数组 是数组的 连续 部分。

示例：

输入：nums = [4,5,0,-2,-3,1]，k = 5

输出：7

输入：nums = [ 5 ]，k = 9

输出：0

二、题解

思路分析

首先我们很容易想到暴力枚举的方法，即遍历数组，在遍历每个元素的同时向后寻找元素之和能够被k整除的子数组

暴力枚举代码如下：

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
       int ret = 0;
       for(int i = 0; i < nums.length; i++){
           int sum = 0;
           for(int j = i; j < nums.length; j++){
               sum += nums[j];
               if(sum % k == 0){
                   ret++;
               }
           }
       }
       return ret;
    }
}

其时间复杂度为O()，当输入的nums数组较大时，会超出时间限制，因此，暴力枚举方式行不通，我们继续考虑其他方法

题目中要求我们找到元素之和可被k整除的（连续、非空）子数组，因此我们可以想到使用双指针的思路，即考虑使用滑动窗口来解决这个问题，然而，本题不能使用滑动窗口来解决

为什么不能使用滑动窗口？

参照示例1，其输入的数组 nums = [4,5,0,-2,-3,1]，其中不仅有正整数，还有零和负数，

在使用滑动窗口时，当窗口内元素满足条件时，要移动left指针，向前滑动窗口，但在本题中，由于有零和负整数，在窗口内元素满足条件时，不能移动left指针，因为下一个元素可能是零，加入后任满足条件，也可能几个元素相加等于0，加入后也满足条件。因此，若是使用滑动窗口来解决本题，则会漏掉一些符合情况的子数组。

滑动窗口的思路也不行，我们继续思考新的方法，在涉及子数组问题时，我们也常使用前缀和来解决问题

什么是前缀和？

前缀和即某序列的前n项和，类似于数学中的数列前n项和。即从首元素位置到i位置这个区间内所有元素之和，前缀和只是一种思路，其不仅可以求和，也可以求从首元素位置到i位置区间内的乘积等等。

我们以示例1为例子，先求前缀和数组，再通过前缀和数组来求解子数组，

然而，在这种情况下，当我们求解子数组时，仍然需要后遍历，求得从i到j位置的元素之和，再判断其是否符合条件，

其时间复杂度仍是O()

在通过前缀和数组求解子数组时，我们可以考虑向前遍历，即i位置上的元素为到i位置的元素之和

此时，若以i位置为结尾的区间内的元素能够被被k整除，则

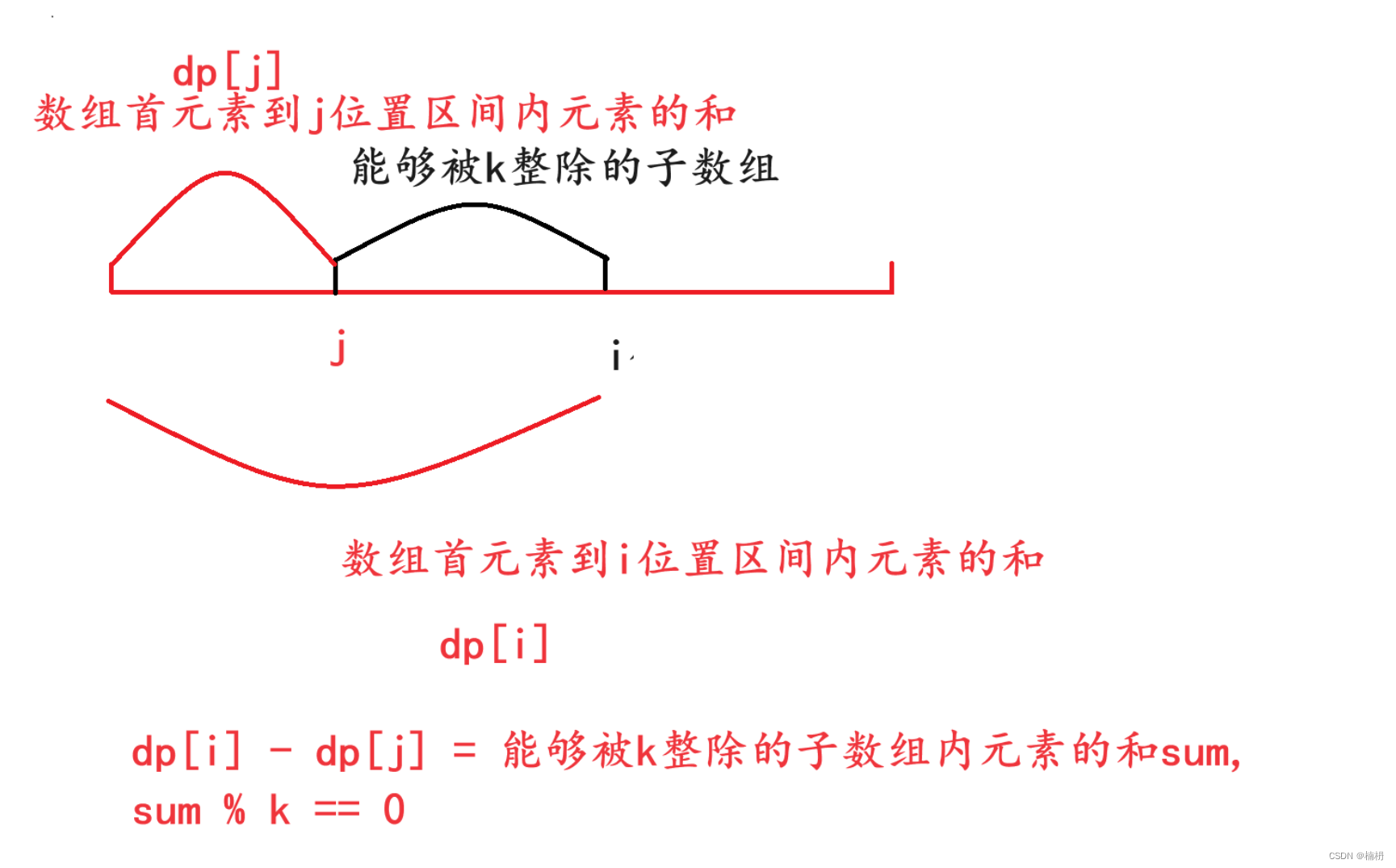
 此时dp[i] - dp[j] = mk，（m为系数），即dp[i]与dp[j]同余(dp[i]取余 k 与dp[j]取余 k 的余数相同）（两数余数相同，在相减时就将余数消去，剩下的数便能整除k)，此时，我们只需要找到，在i位置之前有多少个前缀和元素的余数与其前缀和相同，就能够得到以i位置为结尾的且能够被k整除的子数组个数。

然而，在求i位置之前有多少个前缀和元素的余数与其相同时，我们还需要再向前遍历一遍前缀和数组吗？

我们可以使用哈希表，存储前缀和元素的余数及其个数，这样，便只需要计算dp[i]的余数，再从哈希表中找到相同余数的元素个数，就可知道以i位置为结尾的且能够被k整除的子数组个数了。

在分析完思路后，我们来考虑其具体实现过程：

具体实现

首先我们需要一个哈希表，以前缀和元素模k的值为键，值的个数为值

// key：模k的的值，value：key的个数
Map<Integer, Integer> hash = new HashMap<>();

需要注意的是，在模k时，如果元素为负数，求出的值也为负数（例如 -4 % 5 = -4，-4 与 1 是同余的，若我们在哈希表中保存(-4, 1)，而 % i的结果为 1，并在哈希表中找到结果为1的元素个数，此时就漏掉了结果 为 -4 的情况），

因此我们需要对其进行处理，将其变为正数，可以将其+k，使其变成正数，即 dp[i] % k + k（-4 + 5 = 1）；当其为正数的时候则不需要 +k，若想要无需对元素进行正负数判断，则可在 +k 后再取余k，即 (dp[i] % k + k) % k，此时，若元素为正数，在 +k 后结果大于k，再对结果进行取余，又将其变为正确结果(（3 % 5 + 5）% 5）；若元素为负数，在 +k 后将负数变为正数，即正确结果，再对结果进行取余，仍是正确结果（（-4 % 5 + 5）% 5）

求出数组的前缀和数组

由于哈希表中保存的是模k的值及其个数，因此我们不需要再创建一个前缀和数组用来保存前缀和，只需使用变量sum 来保存前i-1个元素的和

何时将结果放到哈希表中？

我们要从哈希表中找到相同余数的元素个数，从而知道以i位置为结尾的且能够被k整除的子数组个数，因此哈希表中不能存放i位置之后的元素结果，因此，每遍历一个元素，就将其结果更新到哈希表中

然而，此时还有一个细节问题

若以i位置为结尾的数组本身便能被k整除，此时模k的结果为 0，即从0位置到i位置的子数组之和能够被k整除，则在第一次出现该情况时，哈希表内没有key = 0的元素，会漏掉该结果，因此，我们需要处理这种特殊情况，即手动将(0, 1)放入哈希表中

完整代码

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        // key：模k的的值，value：key的个数
       Map<Integer, Integer> hash = new HashMap<>();
       //处理特殊情况
        hash.put(0,1);
        int ret = 0;//子数组的个数
        int sum = 0;//用来保存前i-1个元素之和
        for(int i = 0; i < nums.length; i++){
            sum += nums[i];
            //求出与 前i个元素之和 同余的元素个数
            int same = hash.getOrDefault((sum % k + k) % k, 0);
            ret += same;//更新结果
            hash.put((sum % k + k) % k,same + 1);//更新哈希表
        }
        return ret;
    }
}

题目来自：

974. 和可被 K 整除的子数组 - 力扣（LeetCode）