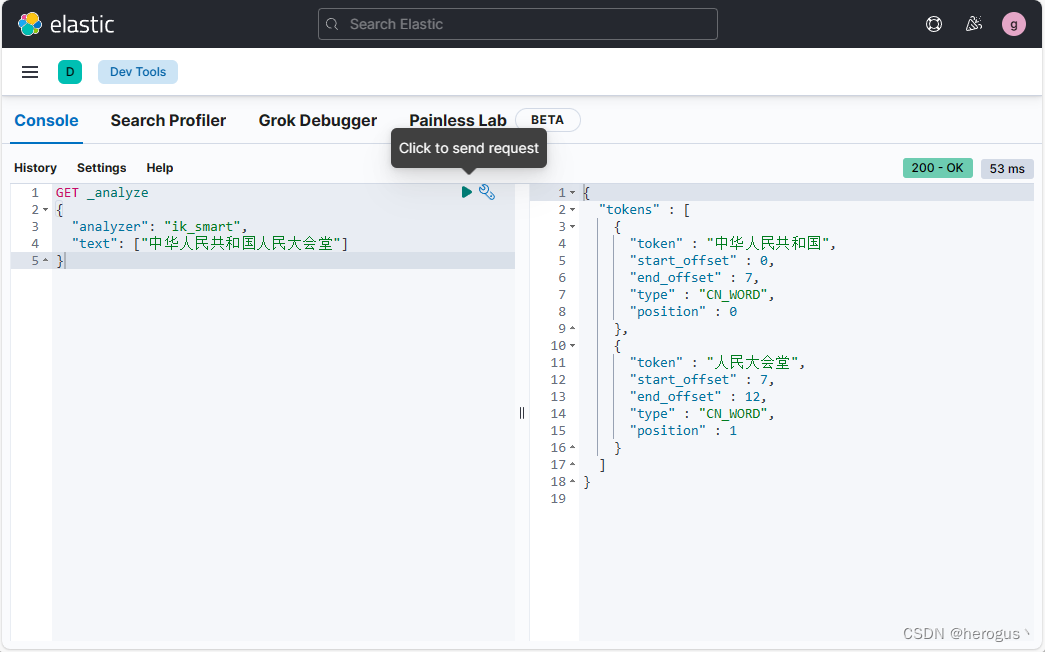
1D、2D或3D线程组织的选择通常基于数据的性质。图片是2D像素阵列。使用由2D块组成的2D网格通常可以方便地处理图片中的像素。图3.2显示了处理76×62图片P的这种安排（水平或x方向为76像素，垂直或y方向为62像素）。假设我们决定使用16 x 16块，x方向有16个线程，y方向有16个线程。我们需要x方向的5个块和y方向的4个块，结果是5个x 4=20个块，如图3.2所示，沉重的线条标志着block的边界。阴影区域描绘了覆盖像素的线程。很容易验证是否可以用公式识别由块（1,0）的线程（0,0）处理的Pin元素：


请注意，我们在x方向有4个额外的线程，在y方向有2个额外的线程——也就是说，我们将生成80×64个线程来处理76×62像素。这种情况类似于图2.11中1D内核vecAddKernel处理1000元素向量的情况。使用四个256线程块。回想一下，需要一个if语句来防止额外的24个线程生效。类似地，我们应该期望图片处理内核函数将有if语句来测试线程索引threadldx.x和threadldx.y是否在有效的像素范围内。

假设主机代码使用整数变量m来跟踪x方向的像素数，另一个整数变量n来跟踪y方向的像素数。我们进一步假设输入图片数据已复制到设备内存中，可以通过指针变量d_Pin访问。输出图片已分配到设备内存中，可以通过指针变量d_Pout访问。以下主机代码可用于启动2D内核colorToGreyscaleConversion来处理图片，如下所示：

dim3 dimGrid(ceil(m/16.0), ceil(n/16.0), 1);
dim3 dimBlock(16, 16, 1);
colorToGreyscaleConversion<<<dimGrid,dimBlock>>>(d_Pin,d_Pout,m,n);

在本例中，为了简单起见，我们假设块的尺寸固定在16×16。与此同时，网格的尺寸取决于图片的尺寸。为了处理2000×1500（3百万像素）的图片，我们将生成11,750个块——x方向的125个，y方向的94个。在内核函数中，对gridDim.x、gridDim.y、blockDim.x和blockDim.y的引用将分别导致125、94、16和16。

记忆空间
内存空间是处理器如何在现代计算机中访问其内存的简化视图。它通常与每个正在运行的应用程序相关联。应用程序要处理的数据和为应用程序执行的指令存储在其内存空间中的位置。通常，每个位置可以容纳一个字节，并且有一个地址。需要多个字节的变量（浮点为4字节，双字节为8字节）存储在连续的字节位置。处理器生成起始地址（起始字节位置的地址）和从内存空间访问数据值时所需的字节数。
内存空间中的位置类似于电话系统中的电话，每个人都有一个唯一的电话号码。大多数现代计算机至少有4G字节大小的位置，其中每个G为1,073,741,824（2^30）。所有位置都标有从0到最大数字的地址。每个位置只有一个地址；因此，我们说内存空间有一个“扁平”的组织。因此，所有多维数组最终都会“扁平化”成等效的一维数组。C程序员可以使用多维语法访问多维数组的元素，而编译器将这些访问转换为指向数组初始元素的基指针，以及从这些多维索引计算的偏移量。

在显示内核代码之前，我们首先需要了解C语句如何访问动态分配的多维数组的元素。理想情况下，我们希望以二维数组的方式访问d_Pin，其中行j和列i的元素可以作为d_Pin[j][i]访问。然而，CUDA C开发所依据的ANSI C标准要求在编译时知道d_Pin中的列数，以便将d_Pin作为2D数组访问。不幸的是，对于动态分配的数组，此信息在编译器时是未知的。事实上，使用动态分配数组的部分原因是允许这些数组的大小和尺寸在运行时根据数据大小而变化。因此，根据设计，在编译时，动态分配的二维数组中的列数信息是未知的。因此，程序员需要将动态分配的二维数组显式线性化或“flatten”为当前CUDA C中等效的一维数组。较新的C99标准允许动态分配数组的多维语法。未来的CUDA C版本可能支持动态分配数组的多维语法。

实际上，由于在现代计算机中使用了“平面”内存空间，C中的所有多维阵列都是线性化的（见“内存空间”侧边栏）。在静态分配的数组中，编译器允许程序员使用更高维的索引语法，如d_Pin[j][i] 来访问他们的元素。在引擎盖下，编译器将它们线性化为等效的一维数组，并将多维索引语法转换为一维偏移量。在动态分配数组中，由于在编译时缺乏维度信息，当前的CUDA C编译器将此类翻译工作留给了程序员。

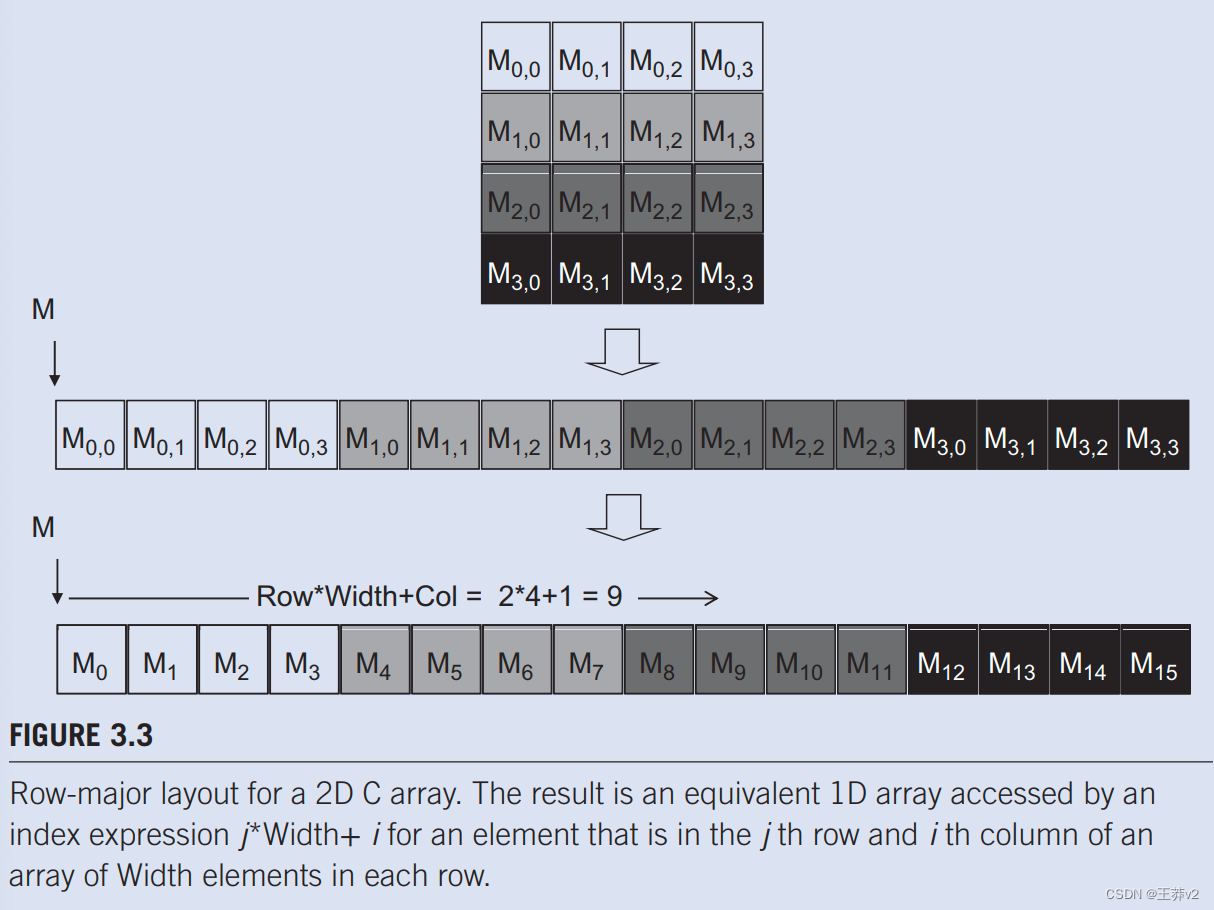
二维数组至少可以通过两种方式线性化。一种方法是将同一行的所有元素放置到连续的位置。然后将行一个接一个地放置在内存空间中。这种安排被称为行主要布局，如图3.3.所示。为了提高可读性，我们将使用Mji来表示j”行和i列的M元素。$P_{j,i}$等价于C表达式M[j][i]，但可读性稍高。图3.3说明了4×4矩阵M如何线性化为16个元素的一维数组，首先是0行的所有元素，然后是第1行的四个元素，以此为例。因此，j行和i列中M的一维等效索引是j4 + i。j4项跳过行j之前行的所有元素。然后，i术语在j行的部分中选择正确的元素。M2.1的一维指数为24 + 1 = 9，如图所示。3.3，其中Mg是M2,1的一维等价物。这个过程展示了C编译器将二维数组线性化的方式。$M_{2,1}$的一维指数为24 + 1 = 9，如图3.3所示，其中$M_9$是$M_{2,1}$的一维等价物。这个过程展示了C编译器将二维数组线性化的方式。

线性化二维数组的另一种方法是将同一列的所有元素放入连续的位置。然后将列一个接一个地放置在内存空间中。这种安排，称为列主要布局，由FORTRAN编译器使用。二维数组的列-主要布局等同于其转置形式的行-主要布局。之前主要编程经验是FORTRAN的读者应该知道，CUDA C使用行主要布局，而不是列主要布局。此外，许多为FORTRAN程序设计的C库使用列主要布局来匹配FORTRAN编译器布局。因此，这些库的手册页，如基本线性代数子程序（BLAS）（见“线性代数函数”侧边栏），通常指示用户从C程序调用这些库时转置输入数组。

线性代数函数
线性代数运算广泛用于科学和工程应用。BLAS是发布执行基本代数运算的库的事实标准，包括三个级别的线性代数函数。随着水平的增加，该函数执行的操作数量也会增加。1级函数执行形式为y =ax + y的向量操作，其中x和y是向量，a是标量。我们的向量加法示例是具有a=1的1级函数的特殊情况。2级函数执行形式为y = αAx + βy的矩阵向量运算，其中A是矩阵，x和y是向量，a是裸标量。我们将研究稀疏线性代数中2级函数的一种形式。3级函数执行C = αAB + βC形式的矩阵矩阵运算，其中A、B、C是矩阵，a、b是标量。我们的矩阵-矩阵乘法示例是3级函数的特殊情况，其中a=1和B=0。这些BLAS函数被用作线性系统求解器和特征值分析等高级代数函数的基本构建块。正如我们稍后将讨论的那样，在顺序和并行计算机中，BLAS函数的不同实现的性能可能因数量级而异。

我们现在准备研究图3.4.中所示的colorToGreyscaleConversion的源代码。内核代码使用公式

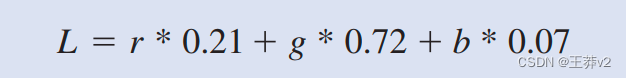
将每个颜色像素转换为灰度对应物。

在水平方向上可以找到总共的blockDim.xgridDim.x线程。与vecAddKernel示例一样，表达式Col=blockIdx.xblockDim.x+threadIdx.x生成从0到blockDim.xgridDim.x-1的每个整数值。我们知道gridDim.xblockDim.x大于或等于宽度（从主机代码传递的m值）。我们的线程数量至少与水平方向的像素数一样多。同样，我们知道线程至少与垂直方向的像素数一样多。因此，只要我们测试并确保只有具有行和Col值的线程在范围内——即（Col<width）&&（Row<height）——我们就可以覆盖图片中的每个像素。

鉴于每行都有宽度像素，因此我们可以为行Row和列Col的像素生成一维索引为Row*width+Col。这个一维索引greyOffset是Pout的像素索引，因为输出灰度图像中的每个像素都是一个字节（无符号字符）。通过使用我们的76×62图像示例，Pout像素的线性化一维索引由块（1,0）的线程（0,0）计算，公式为：

至于Pin，我们将灰色像素索引乘以3，因为每个像素存储为（r，g，b），每个像素等于一个字节。生成的rgboffset给出了Pin数组中颜色像素的起始位置。我们从Pin数组的三个连续字节位置读取r、g和b值，执行灰度像素值的计算，并使用greyOffset将该值写入Pout数组。在我们的76×62图像示例中，引脚像素的线性化一维索引由块（1,0）的线程（0,0）计算，公式如下：


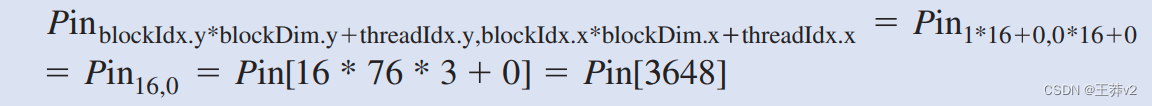
正在访问的数据是三个字节，从字节索引3648开始。

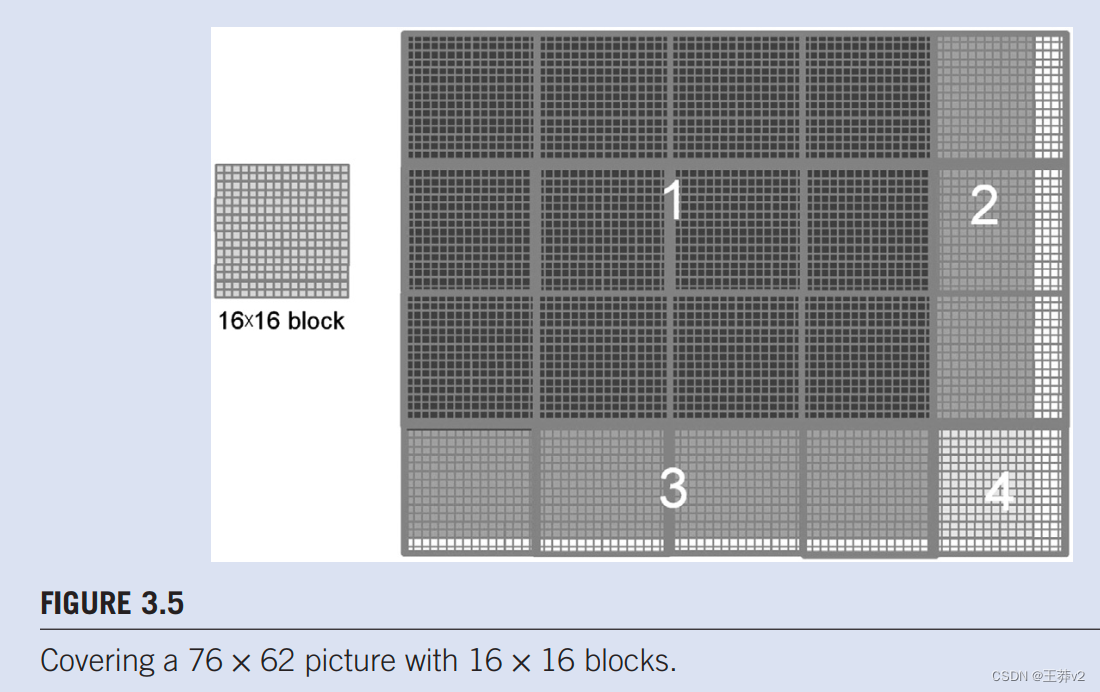
图3.5说明了在处理我们的76×62示例时执行colorToGreyscaleConversion。假设我们使用16×16块，启动colorToGreyscaleConversion会生成80 x 64线程。网格将有20个块——5个水平方向，4个垂直方向。块的执行行为将分为四种不同情况之一，在图3.5.中描述为四个阴影区域。

第一个区域，在图3.5中标记为“1”，由属于覆盖图片中大部分像素的12个块的线程组成。这些线程的Col和Row值都在范围内；所有这些线程都将通过if-statement测试，并在图片的阴影严重区域处理像素——即每个块中的所有16×16=256线程都将处理像素。第二个区域，在图中标记为“2”。3.5，包含属于覆盖图片右上角像素的中等阴影区域中三个块的线程。虽然这些线程的行值总是在范围内，但一些Col值超过m值（76）。原因是水平方向的线程数总是程序员选择的blockDim.x值的倍数（在本例中为16）。覆盖76像素所需的16的最小倍数是80。因此，每行中的12个线程将具有范围内的Col值，并将处理像素。与此同时，每行中的4个线程将具有不在范围内的Col值，因此无法满足if-statement条件。这些线程不会处理任何像素。总体而言，每个块中的16×16=256个线程中的12×16=192将处理像素。

第三个区域，在图中标记为“3”。3.5，占了3个左下角的blocks，覆盖了图片中的中等阴影区域。虽然这些线程的Col值总是在范围内，但一些行值超过m值（62）。原因是垂直方向的线程数总是程序员选择的blockDim.y值的倍数（在这种情况下是16）。覆盖62的16的最小倍数是64。因此，每列中的14个线程将具有范围内的行值，并将处理像素。与此同时，每列中的2个线程将失败区域2的if-statement，并且不会处理任何像素。在256个线程中，16×14 = 224将处理像素。第四个区域，在图中标记为“4”。3.5，包含覆盖图片右下角、轻度阴影区域的线程。在前14行中的每行中，4个线程的Col值将处于范围之外，类似于区域2。该块的整个底部两行将具有范围之外的行值，类似于区域“3”。因此，16 × 16 = 256个线程中只有14 x 12 = 168将处理像素。

当我们线性化数组时，我们可以通过包括另一个维度，轻松地将2D数组的讨论扩展到3D数组。这是通过将数组的每个“plane”一个接一个地放入地址空间来实现的。假设程序员使用变量m和n来跟踪3D数组中的列数和行数。程序员在启动内核时还需要确定b1ockDim.z和gridDim.z的值。在内核中，数组索引将涉及另一个全局索引：

int Plane = blockIdx.z*blockDim.z + threadIdx.z

对三维数组P的线性访问将以P[Planemn+Row*m+Col]的形式进行。处理3D P阵列的内核需要检查所有三个全局索引（Plane、Row和Co1）是否都在数组的有效范围内。