题目链接

1 前言

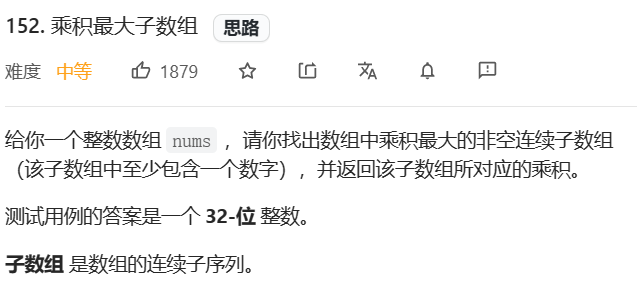
翻译成大白话：就是找一个数组，其连续子数组的乘积最大值。

2 算法思路：

一般求最值的问题首选动态规划。

这道题与[LC.53 最大子序和]很类似。我们假设状态转移方程为:

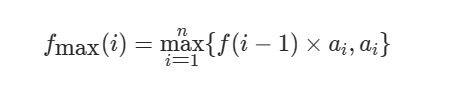
它表示以第 i 个元素结尾乘积最大子数组的乘积

可是在这里，这样做是错误的。为什么呢？

因为这里的定义并不满足「最优子结构」。具体地讲，如果 a = {5, 6, −3, 4, −3}，那么此时 f(i)对应的序列是 {5,30,-3,4,-3}，按照前面的算法我们可以得到答案为 30，即前两个数的乘积，而实际上答案应该是全体数字的乘积。我们来想一想问题出在哪里呢？问题出在最后一个 -3。所以我们得到了一个结论：当前位置的最优解未必是由前一个位置的最优解转移得到的。

我们可以根据正负性进行分类讨论。

由于负数存在的原因，我们可根据负数分类，使用来个动态数组。

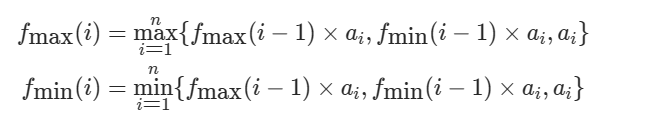
中记录的是以第 i 个元素结尾乘积最大子数组的乘积。

中记录的是以第 i 个元素结尾乘积最小子数组的乘积。

3 具体代码

package cn.msf.hot100;

/**
 * @author : msf
 * @date : 2023/1/3
 * lc.152:乘积最大子数组：应该是用动态规划
 */
public class MaxProduct {
    public static void main(String[] args) {
        int[] nums = {2, 3, -2, 4};
        int res = new MaxProduct().maxProduct(nums);
    }

    public int maxProduct(int[] nums) {
        int n = nums.length;
        // 定义dp[i]：从nums[...i]为止，乘积最小的子数组。
        int[] dp = new int[n];
        // 定义dp[i]：从nums[...i]为止，乘积最大的子数组。
        int[] dp1 = new int[n];
        // base case
        dp[0] = nums[0];
        dp1[0] = nums[0];
        for (int i = 1; i < n; i++) {
            // 在不考虑0的前提下，如果考虑0 则需要将nums[i]考虑
            // 如果有nums[i]<0，那么dp1[i-1] * 负值 = dp[i].
            dp[i] = min(dp[i - 1] * nums[i], dp1[i - 1] * nums[i], nums[i]);
            // 如果是正值，那么dp1[i-1] * 正值最大。 如果是负值，那么dp[i-1] * 负值肯定是最大。
            dp1[i] = max(dp[i - 1] * nums[i], dp1[i - 1] * nums[i], nums[i]);
        }
        // 遍历所有子数组的最大乘积，求最大值
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < n; i++) {
            res = Math.max(res, dp1[i]);
        }
        return res;
    }

    int min(int a, int b, int c) {
        return Math.min(Math.min(a, b), c);
    }

    int max(int a, int b, int c) {
        return Math.max(Math.max(a, b), c);
    }
}