文章目录
- 1. AOE网
- 2. 拓扑排序
- C++代码
1. AOE网
AOV网∶若用DAG 图(有向无环图)表示一个工程,其顶点表示活动,用有向边<Vi,Vj>表示活动 Vi必须先于活动Vj进行的这样一种关系,则将这种有向图称为顶点表示活动的网络,记为 AOV网。
在AOV网中,活动Vi是活动Vj的直接前驱,活动Vj是活动Vi的直接后继,这种前驱和后继关系具有传递性,且任何活动V不能以它自己作为自己的前驱或后继
2. 拓扑排序
拓扑排序∶在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序∶
- 每个顶点出现且只出现一次。
- 若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。
或定义为∶
拓扑排序是对有向无环图的顶点的一种排序,它使得若存在一条从顶点A到顶点
B的路径,则在排序中顶点B出现在顶点A的后面。
每个AOV 网都有一个或多个拓扑排序序列。
对一个AOV 网进行拓扑排序的算法有很多,下面介绍比较常用的一种方法的步骤:
- 从AOV网中选择一个没有前驱的顶点并输出。
- 从网中删除该顶点和所有以它为起点的有向边。
- 重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
eg:
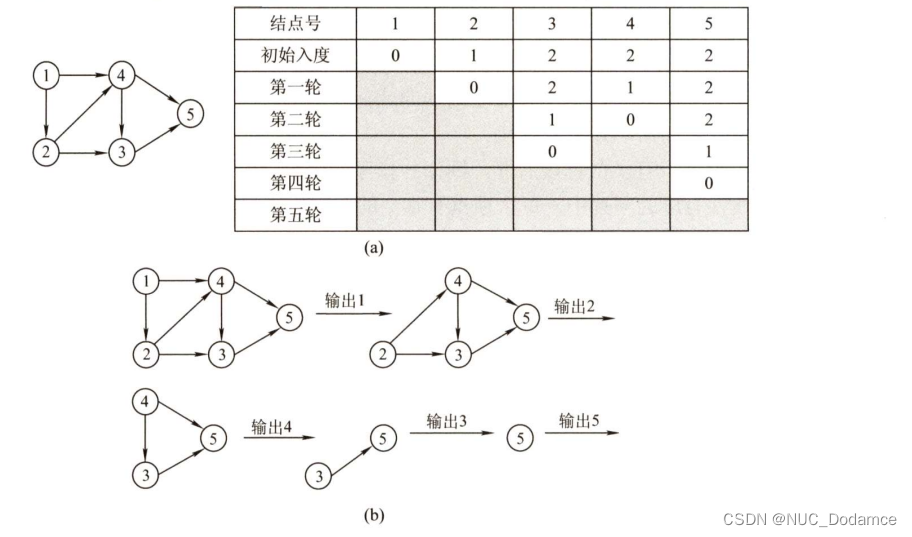
拓扑排序结果1,2,4,3,5
C++代码
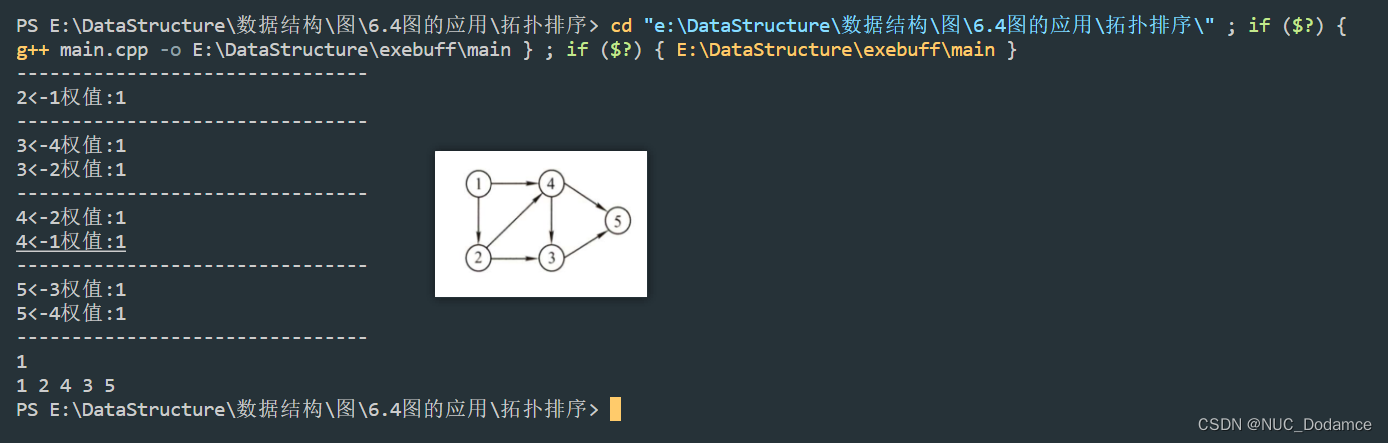
图采用邻接表储存,
由于输出每个顶点的同时还要删除以它为起点的边,故采用邻接表存储时拓扑排序的时间复杂度为O(V+E),采用邻接矩阵存储时拓扑排序的时间复杂度为 O(V2)
#include <iostream>
#include <vector>
#include <assert.h>
#include <unordered_map>
#include <stack>
template <class w>
struct Edge
{
int srcPos = -1;
w weight; // 权值
Edge<w> *next;
Edge(int _srcPos, const w &_weight) : srcPos(_srcPos), weight(_weight), next(nullptr) {}
};
// v:节点的值,w节点的权值 flag==false为无向图
template <class v, class w, bool flag = false>
class linkTable
{
typedef Edge<w> Edge;
private:
std::vector<Edge *> _matrix; // 邻接表
std::unordered_map<v, int> _indexMap; // 保存图节点对应邻接表数组的下标
std::vector<v> _points; // 顶点集合
int _getPointPos(const v &point)
{
typename std::unordered_map<v, int>::iterator pos = _indexMap.find(point);
if (pos == _indexMap.end())
return -1; // 没找到
return pos->second;
}
public:
linkTable(const std::vector<v> &src)
{
int size = src.size();
assert(size > 0);
_points.resize(size);
for (int i = 0; i < size; i++)
{
_points[i] = src[i];
_indexMap[src[i]] = i;
}
_matrix.resize(size, nullptr);
}
// 添加边的关系,储存入度边
void AddEdge(const v &src, const v &dst, const w &weight)
{
int posSrc = _getPointPos(src);
int posDst = _getPointPos(dst);
assert(posSrc >= 0 && posSrc >= 0);
// 构建Edge,头插到数组上
Edge *edge = new Edge(posSrc, weight);
edge->next = _matrix[posDst];
_matrix[posDst] = edge;
if (!flag)
{
// 无向图,两条边都要构建
edge = new Edge(posSrc, weight);
edge->next = _matrix[posSrc];
_matrix[posSrc] = edge;
}
}
// 打印邻接表信息
void PrintGraph()
{
for (int i = 0; i < _matrix.size(); i++)
{
Edge *edge = _matrix[i];
while (edge != nullptr)
{
std::cout << _points[i] << "<-";
std::cout << _points[edge->srcPos] << "权值:" << edge->weight << std::endl;
edge = edge->next;
}
std::cout << "--------------------------------" << std::endl;
}
}
//---------------------------拓扑排序-----------------
/**
* @brief 返回图的拓扑排序是否完成
*
* @param buff 有向无环图的拓扑排序结果数组
* @return true 这个图是完成了拓扑排序
* @return false 这个图带环,没有拓扑排序
*/
bool Topological(std::vector<v> &buff)
{
std::stack<v> st;
std::vector<bool> visit(_points.size(), false); // 判断这个节点是否被访问过
// 储存入度为0节点
for (size_t i = 0; i < _matrix.size(); ++i)
{
if (_matrix[i] == nullptr)
{
st.push(i);
visit[i] = true;
}
}
int count = 0;
while (!st.empty())
{
int top = st.top();
buff.push_back(_points[top]);
st.pop();
count++;
// 将所有top指向的顶点度-1,如果度为0继续入栈
for (size_t i = 0; i < _matrix.size(); i++)
{
if (_matrix[i] != nullptr)
{
Edge *node = _matrix[i];
Edge *prev = nullptr;
while (node != nullptr)
{
if (node->srcPos == top)
{
if (prev == nullptr)
{
// 头删
_matrix[i] = node->next;
delete node;
node = _matrix[i];
}
else
{
prev->next = node->next;
delete node;
node = prev->next;
}
}
else
{
prev = node;
node = node->next;
}
}
}
}
// 储存入度为0节点
for (size_t i = 0; i < _matrix.size(); ++i)
{
if (_matrix[i] == nullptr && visit[i] == false)
{
st.push(i);
visit[i] = true;
}
}
}
return _points.size() == count;
}
};
#include "topological.h"
int main(int argc, char const *argv[])
{
linkTable<char, int, true> graph({'1', '2', '3', '4', '5'});
graph.AddEdge('1', '4', 1);
graph.AddEdge('1', '2', 1);
graph.AddEdge('2', '4', 1);
graph.AddEdge('2', '3', 1);
graph.AddEdge('4', '3', 1);
graph.AddEdge('4', '5', 1);
graph.AddEdge('3', '5', 1);
graph.PrintGraph();
std::vector<char> buff;
std::cout << graph.Topological(buff) << "\n";
for (auto num : buff)
{
std::cout << num << " ";
}
return 0;
}
对一个AOV网,如果采用下列步骤进行排序,则称之为逆拓扑排序∶
- 从AOV网中选择一个没有后继(出度为0)的顶点并输出。
- 从网中删除该顶点和所有以它为终点的有向边。
- 重复1和2直到当前的AOV网为空。
用拓扑排序算法处理 AOV网时,应注意以下问题;
- 入度为零的顶点,即没有前驱活动的或前驱活动都已经完成的顶点,工程可以从这个顶点所代表的活动开始或继续。
- 若一个顶点有多个直接后继,则拓扑排序的结果通常不唯一,但若各个顶点已经排在一个线性有序的序列中,每个顶点有唯一的前驱后继关系,则拓扑排序的结果是唯一的。
- 由于AOV网中各顶点的地位平等,每个顶点编号是人为的,因此可以按拓扑排序的结果重新编号,生成 AOV 网的新的邻接存储矩阵,这种邻接矩阵可以是三角矩阵但对于一般的图来说,若其邻接矩阵是三角矩阵,则存在拓扑序列;反之则不一定成立
使用DFS算法递归的遍历一个无环有向图,在退出递归时输出响应的顶点,这样得到的序列时这个图的逆拓扑排序序列
图的深度优先遍历有一个特点:
当一个顶点的子结点都被访问完了,该顶点才会结束访问,并开始向上回溯访问它的父结点的其它子结点。
这意味着,一个顶点的结束访问时间与其子结点的结束访问时间存在先后关系,而这个顺序刚好与拓扑排序是相反的!
简单地说,在深度优先遍历中,顶点A要结束访问的前提是其子结点B、C、D…都被访问完了,而在拓扑排序中,事件A完成之后其后面的事件B、C、D…才可以继续进行。这也就是上面的深度优先搜索为什么要记录结点被访问完成的次序,因为这个次序倒过来就是拓扑排序的顺序!