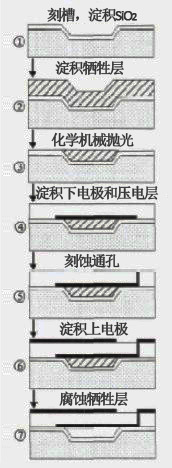
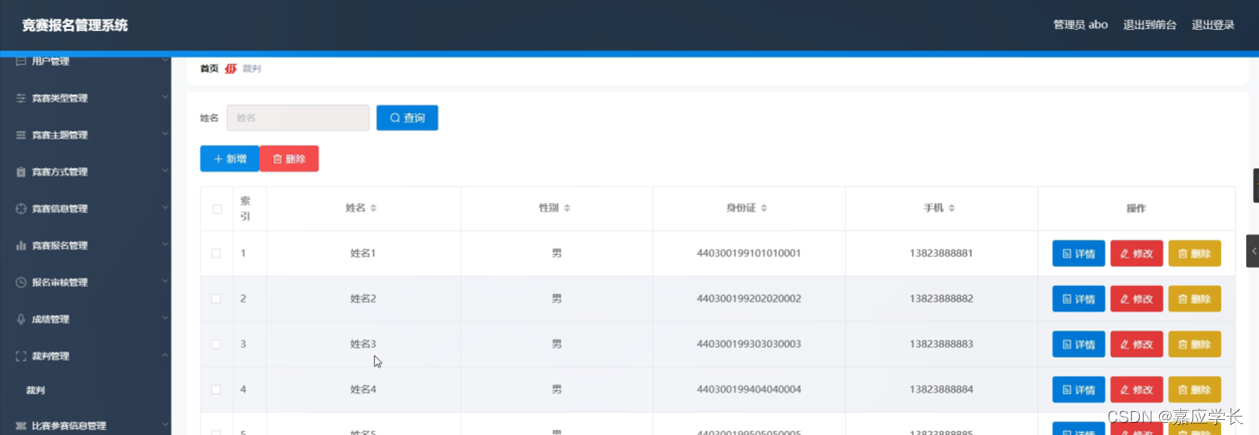
如果有错误请及时指出,大家一起学习交流。
目录
一、PID的概述
二、PID三个参数的控制原理
1、P控制器
2、I控制器
3、D控制器
4、PID控制器
5、PID的数学公式
三、位置式PID和增量式PID的差别和代码实现
1、位置式PID和增量式PID的差别
2、位置式PID
3、增量式PID
一、PID的概述
将采集的实际值与给定的目标值进行比较,对产生的偏差用比例、积分和微分进行控制的控制系统,简称PID(Proportional Integral Derivative)控制系统,也是大学里面用得较多的算法之一,比如做一些匀速行驶的小车或者是一些恒温系统都能见到PID的身影。
比例(P)控制能迅速反应误差,从而减小稳态误差。但是并不能消除稳态误差。比例放大系数的加大.会引起系统的不稳定。
积分(I)控制器的作用是只要系统有偏差存在,积分控制器就会不断地积累偏差,输出控制量,以消除偏差。也就是说,只要有足够的时间,积分控制器就能完全消除误差,使系统误差为零,从而消除稳态误差。但是积分项太强会使系统出现超调加大,或者使系统出现振荡。
微分(D)控制器可以减小超调量,克服振荡,使系统的稳定性提高,同时加快系统的动态响应速度.减小调整时间,从而改善系统的动态性能。
根据不同的被控对象的控制特性,又可以分为P、PI、PD、PID等不同的控制模型。
二、PID三个参数的控制原理
首先说明一下用到的参数含义以及一些原理
target:目标值,也就是小车需要达到的目标速度值。
practical:实际值,也就是小车当前行驶的实际速度。
error:偏差值,也就是目标值 - 实际值(error = target - practical)。
设当前有一个测试温度的系统,到达规定时间 t 就返回一个当前的实际温度值T(x),即可得到集合{T(x1),T(x2),T(x3)......T(n-1),T(xn)},来分别表示返回来的温度值。
1、P控制器
由error = target - T(x) 可以得到温度的偏差值,即目标温度值 - 实际温度值,
得,当 error > 0时:表示目标值大于实际值,即当前控制未达到预期要求。
当error = 0时:表示目标值等于实际值,即当前控制刚好达到预期要求。
当error < 0时:表示目标值小于实际值,即当前控制超过预期要求。
P控制器是通过error来输出信号的 ,即输出公式为
Pout = Kp * error
也就是输出信号和和当前的偏差值成正比关系。Kp为比例系数,当Kp > 0时,输出为正,此时为一个放大器,当Kp < 0时,输出为负,此时为一个衰减器,Kp = 0时,输出为0,此时的系统已经脱离了控制,也就是说P控制器是一个始终有偏差的控制器,有偏差才控制,没有偏差就不关我的事,输出为0就好。
2、I控制器
由上面P控制器得到实际温度 T(x) 的集合{T(x1),T(x2),T(x3)......T(x-1),T(xn)},以及设置的目标温度值 target 可得当前所有偏差的集合{Error(x1),Error(x2),Error(x3)......Error(n-1),Error(xn)},(Error = target - T(x) )。
设偏差和用SumError表示
则 SumError = Error(x1) + Error(x2) + Error(x3) + ...... + Error(n-1) + Error(xn)
当SumError > 0 时,整体的偏差大于0,说明在过去的一段时间里大部分参数是没有达标的。
当SumError = 0 时,整体的偏差等于0,说明在过去的一段时间里控制效果是达到了标准的。
当SumError < 0 时,整体的偏差小于0,说明在过去的一段时间里大部分参数是超过目标值的。
I控制器公式:
Iout = Kp * SumError
也就是说积分控制器的输出和总的偏差值是成正比关系的。Iout 为积分控制器的输出,Ki为比例系数,SumError为偏差和。
如果大部分参数没达标,那积分控制器就会输出一个正值,来增强输出,即SumError 是大于0 的,如果大部分参数都超过目标值,那么积分控制器会输出负值,来削弱输出,即SumError是小于0的。
积分控制器就是需要看以前一段时间的总偏差值,当前是否合适都没关系,它是看以前怎么样。
3、D控制器
和 I 控制器一样,实际温度 T(x) 的集合{T(x1),T(x2),T(x3)......T(x-1),T(xn)},由设置的目标温度值 target 可得当前所有偏差的集合{Error(x1),Error(x2),Error(x3)......Error(n-1),Error(xn)}。
设当前偏差为Error(n),前一时刻偏差为 Error(n -1),设偏差的差值用 ErrorSubtract 表示
则 ErrorSubtract = Error(n) - Error(n-1),ErrorSubtract的值是表示两个时刻偏差的变化趋势。
当 ErrorSubtract > 0 时,也是当前偏差比上一次的偏差还要大,系统会越来越偏离目标值。
当 ErrorSubtract = 0 时,也就是当前偏差和上一次偏差相等,系统没有变化。
当 ErrorSubtract < 0 时,也就是当前偏差比上一次偏差要小,偏差有变小的趋势,系统会越来越接近目标值。
D控制器公式:
Dout = Kp * ErrorSubtract , 即D控制器的输出是和偏差的差成正比关系。
4、PID控制器
PID控制器就是将三个控制器加起来就得到PID控制器,即PIDout = Pout + Iout + Dout
即可得到 PID 的数学公式
其中 out 是为了不让系统失控,也就是为了不让系统输出为 0 。
SumError 和 ErrorSubtract 的整理
(1)SumError
Ti表示积分时间常数,也指积分项的运行时间,T表示计算周期,也就是更新PID的时间,Ti越大输出越小。
(2)ErrorSubtract
Td表示微分时间常数,也指微分的运行时间,T表示计算周期,也就是多久更新计算一下PID。
5、PID的数学公式
有上面可的PID的数学公式为
其中:PIDout 为控制系统的输出值,error(t)为偏差信号,Kp 为比例项系数,Ki = Kp * (1 / Ti) * T 为积分项系数,Kd = Kp * Td * 1/T 为微分项系数。
根据上述公式可写出如下代码
float Error,lastError, //本次偏差,上次偏差
float IntegralError,DifferentialError, //偏差的积分,偏差的微分
float ProportionOut,IntegralOut,DifferentialOut, //比例项输出,积分项输出,微分项输出
float T,Ti,Td, //控制周期,积分时间常数,微分时间常数
float PidOut; //PID最终输出
float Kp,Ki,Kd; //比例项系数,积分项系数,微分项系数
int PID_Controller(float Target,float practical)
{
Ki = Kp * T * (1/Ti); //积分项系数
Kd = Kp * Td * (1/T); //微分项系数
Error = Target - practical; //偏差
IntegralError = IntegralError + Error; //偏差的积分
DifferentialError = Error - lastError; //偏差的微分
ProportionOut = Kp * Error; //比例项输出 = Kp * 偏差
IntegralOut = Ki * IntegralError; //积分项输出 = Ki * 偏差的积分
DifferentialOut = Kd * DifferentialError; //微分项输出 = Kd * 偏差的微分
PidOut = ProportionOut + IntegralOut + DifferentialOut; //三个项相加
return PidOut; //返回PID计算值
}三、位置式PID和增量式PID的差别和代码实现
1、位置式PID和增量式PID的差别
这两种PID算法最大的差别就是位置式PID的输出与整个过去的状态都是有关的,用到了误差的累加值,也就是用到了积分运算,而增量式PID的输出只与当前误差以及前两次的误差有关,和以前的误差无关,没有积分的作用。
2、位置式PID
公式如下:
比例项e(k):偏差,即目标值 - 实际值。
积分项∑e(i):偏差的累加。
微分项e(k) - e(k-1):偏差的差,即这次偏差 - 上一次偏差。
即当前系统的实际位置,与你想要达到的目标位置的偏差,来进行PID计算控制。
有积分 ∑e(i)的加入,偏差会一直累加,也就是当前的输出与过去的所有状态都有关系,用到了偏差的累加值,位置式PID在积分项达到饱和时误差依然会继续累积,一旦误差开始反向变化,系统则需要一定的时间从饱和区中退出,所以在输出达到最大值或最小值时,要停止积分的作用,并且要有积分限幅和输出限幅的加入,在使用位置式PID时,一般直接使用PD控制,而避免了积分项的影响,位置式 PID 适用于执行机构不带积分部件的对象,如舵机和平衡小车的直立和温控系统的控制。
参考代码如下:
float Error,lastError, //本次偏差,上次偏差
float IntegralError,DifferentialError, //偏差的积分,偏差的微分
float ProportionOut,IntegralOut,DifferentialOut, //比例项输出,积分项输出,微分项输出
float PidOut; //PID最终输出
float Kp,Ki,Kd; //比例项系数,积分项系数,微分项系数
int PID_Controller(float Target,float practical)
{
Error = Target - practical; //偏差
IntegralError = IntegralError + Error; //偏差的积分
DifferentialError = Error - lastError; //偏差的微分
ProportionOut = Kp * Error;
IntegralOut = Ki * IntegralError;
DifferentialOut = Kd * DifferentialError;
PidOut = ProportionOut + IntegralOut + DifferentialOut; //三个项相加
return PidOut; //返回PID计算值
}3、增量式PID
公式如下:
比例项e(k)-e(k-1):偏差的差,即当前偏差 - 上次偏差
积分项e(i):偏差
微分项e(k) - 2e(k-1)+e(k-2):当前这次的偏差 - 2倍上次偏差 + 上上次的偏差
由增量式PID的公式可以看出,如果确定了 Kp、Ki 、Kd的值,再使用计算的三次的偏差, 即可求出输出量。
增量式PID得出的输出量是对应的近几次的偏差增量,而不是对应与实际位置的偏差,并没有误差的累加,也就是说增量式PID是取的增量,并不需要累积误差,输出只与近3次的采样值有关,减少控制量。
参考代码如下:
float LastError = 0; //Error[-1]
float PrevError = 0; //Error[-2]
double Proportion; //比例常数 Proportional Const
double Integral; //积分常数 Integral Const
double Derivative; //微分常数 Derivative Const
int PID_Calc(int NextPoint,int SetPoint)
{
float Error,Outpid;
iError = SetPoint - NextPoint; //偏差计算
Outpid = (Proportion * Error) //E[k]
-(Integral * LastError) //E[k-1]
+(Derivative * PrevError); //E[k-2]
PrevError = LastError; //存储误差
LastError = Error;
return Outpid; //返回输出
}
![[C++基础]-初识模板](https://img-blog.csdnimg.cn/b6aa563e84fe47acb989c952444f798d.png)