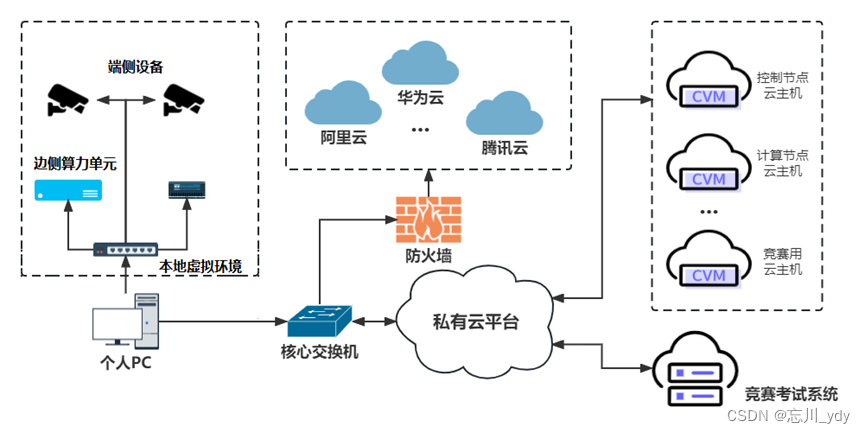
倍增法

倍增法（Binary Lifting），顾名思义，就是利用“以翻倍的速度增长”的思想来解决问题的一类算法，它能够使线性的处理转化为对数级的处理，大大地优化时间复杂度。这个方法在很多算法中均有应用，其中最常用的是 RMQ 问题和求 LCA（最近公共祖先）。

下面介绍如何使用倍增法在有序的序列中查找满足条件的位置。

题目描述

给定一个单调不降的序列，以及$m$个查询，每个查询是一个数字$k$，查找第一个大于等于$k$的位置。

输入格式

第一行 $n$ 和 $m$；

第二行 $n$ 个元素的序列；

第三行 $m$ 个数字，表示 $m$ 个查询的 $k$， 每个查询的 $k$，确保在序列的最大值范围内。

输出格式

$m$ 个数字，表示第一个大于等于 $k$ 的位置，用空格隔开。

样例输入

10 1 
1 2 3 4 6 6 6 8 9 10
6

样例输出

5

数据范围

• 20%的数据，$1\le n,m\le 1000$
• 100%的数据，$1\le n,m\le 10^5$，$1\le$所有元素$\le 10^9$，所有$1\le k\le$序列最大值

算法思想

在单调不降的序列中查找一个大于等于 $k$ 的位置，朴素的做法是从位置$1$开始判断，不满足要求则每次向右移动$1$个位置，重复进行直到找到满足条件的位置，时间复杂度为$O(n)$。

倍增法也从位置$1$开始判断，如果该位置上的数小于 $k$，则将移动的距离增加$1$倍，然后向右移动；否则，如果该位置上的数大于等于$k$，则将移动的距离减半，继续判断。重复进行直到不能移动为止，时间复杂度为$O(logn)$。

移动过程如下图所示：

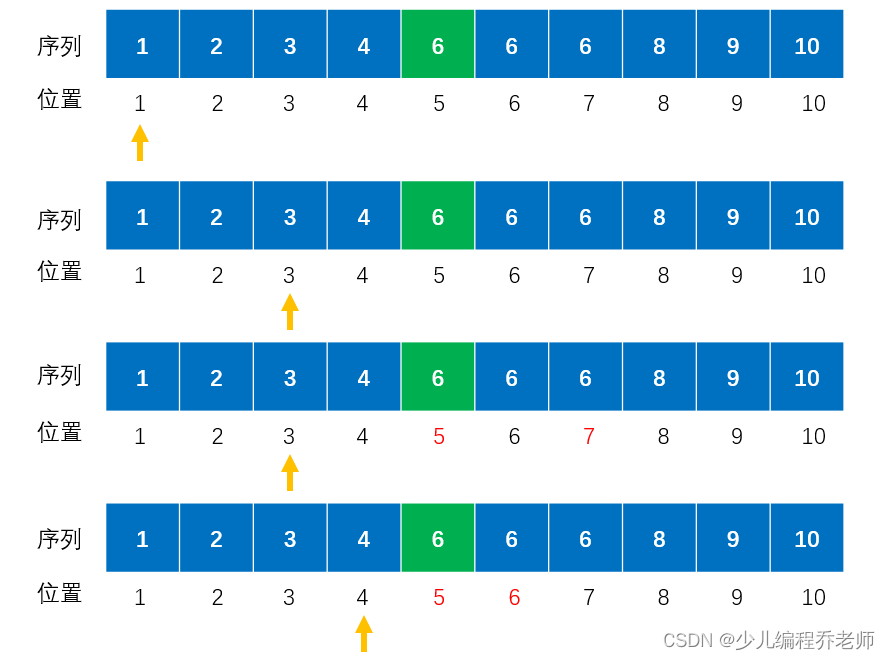
查找结束后会停留在最后一个小于$k$的位置上。

代码实现

#include <iostream>
using namespace std;
const int N = 5e5 + 10;
int a[N];
int main()
{
    int n, m, k;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++) scanf("%d", a + i);
    while(m --) {
        scanf("%d", &k);
        //x表示位置，p表示增加距离
        int x = 0, p = 1;
        while(p != 0) {
        	//x位置上的数小于k，则将移动的距离增加1倍
            if(x + p <= n && a[x + p] < k) {
                x += p;
                p *= 2;
            }
            //x位置上的数大于等于k，则将移动的距离减半
            else p /= 2;
        }
        //x最终停留在最后一个小于k的位置上，应输出x + 1
        printf("%d ", x + 1); 
    }
}