一、基本概述
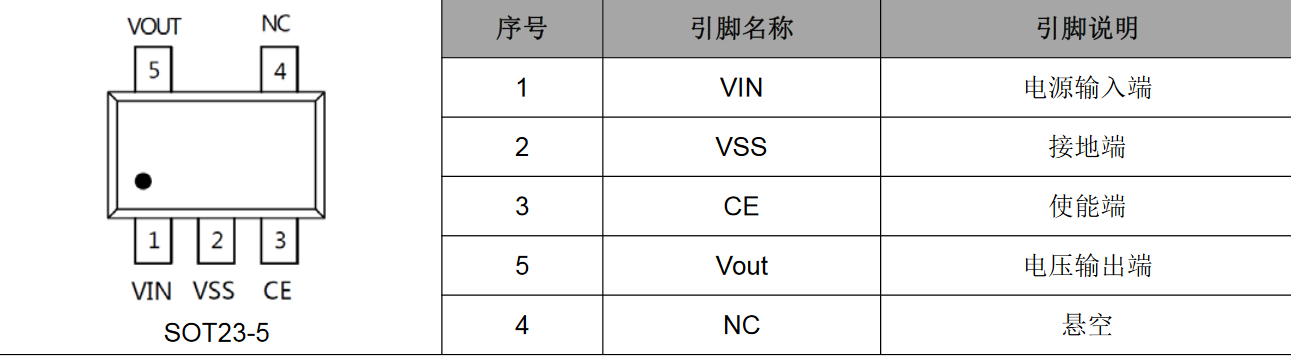
FM6215 系列采用 CMOS 工艺制造的高精度、低功耗低压差稳压器。该系列具有极低的静态电流, 输出电压 3.3v的产品静态功耗仅为 0.9uA(TYP),最大输出电流可达到 300mA。 产品采用 SOT23-5 封装,因此,该系列适用于需要高密度安装的应用场合,例如便携式移动设备。
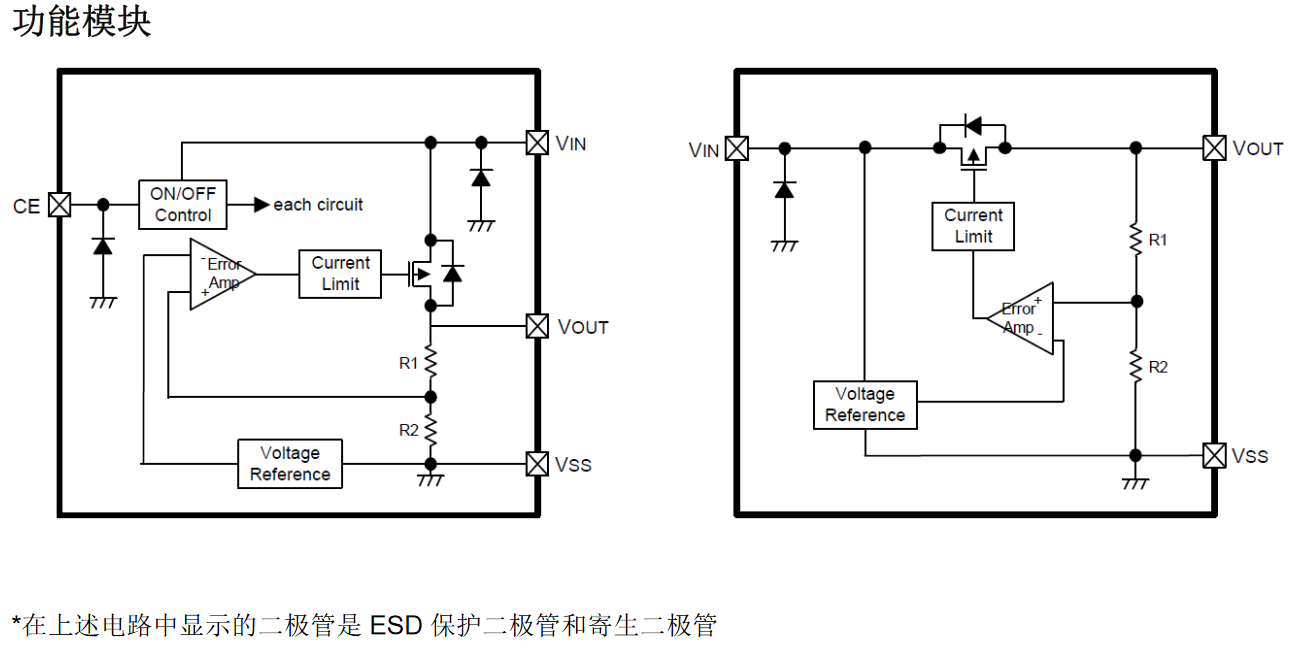
该系列产品可根据客户需要选择 1.2V ~ 5.0V 的输出电压。该系列产品还可使用低 ESR 陶瓷电容器增加输出稳定性。芯片内置折返式限流电路,可有效保护负载短路等异常情况。此外,CE 使能可允许关闭 LDO 的输出,从而进一步降低了系统功耗。
二、产品特性
-
输出电流能力:200mA(,最大值 300mA,@Vout= 3.3V,VIN = 4.3V)
-
输入输出电压差:320mV @ Iout = 100mA Vout= 3.3V
-
输入电压范围:1.5V ~ 6.0V
-
输出电压范围:1.2V ~ 5.0V(0.1V 增量)
-
输出电压精度::±2% @1.5V<Vout≤5.0V
-
±30 mv@1.2V≤Vout≤1.5V
-
低静态功耗:0.9uA(TYP)@Vout=3.3v。待机电流:小于 0.1uA
-
工作温度范围:- 40℃~ 85℃
-
低 ESR 电容兼容:陶瓷电容器
-
内置限流器电路
-
封装形式:SOT23-5

三、产品应用
-
智能手机/移动电话
-
便携式游戏机
-
数码相机/摄像机
-
数字音频设备
-
移动设备/终端
四、电特性指标

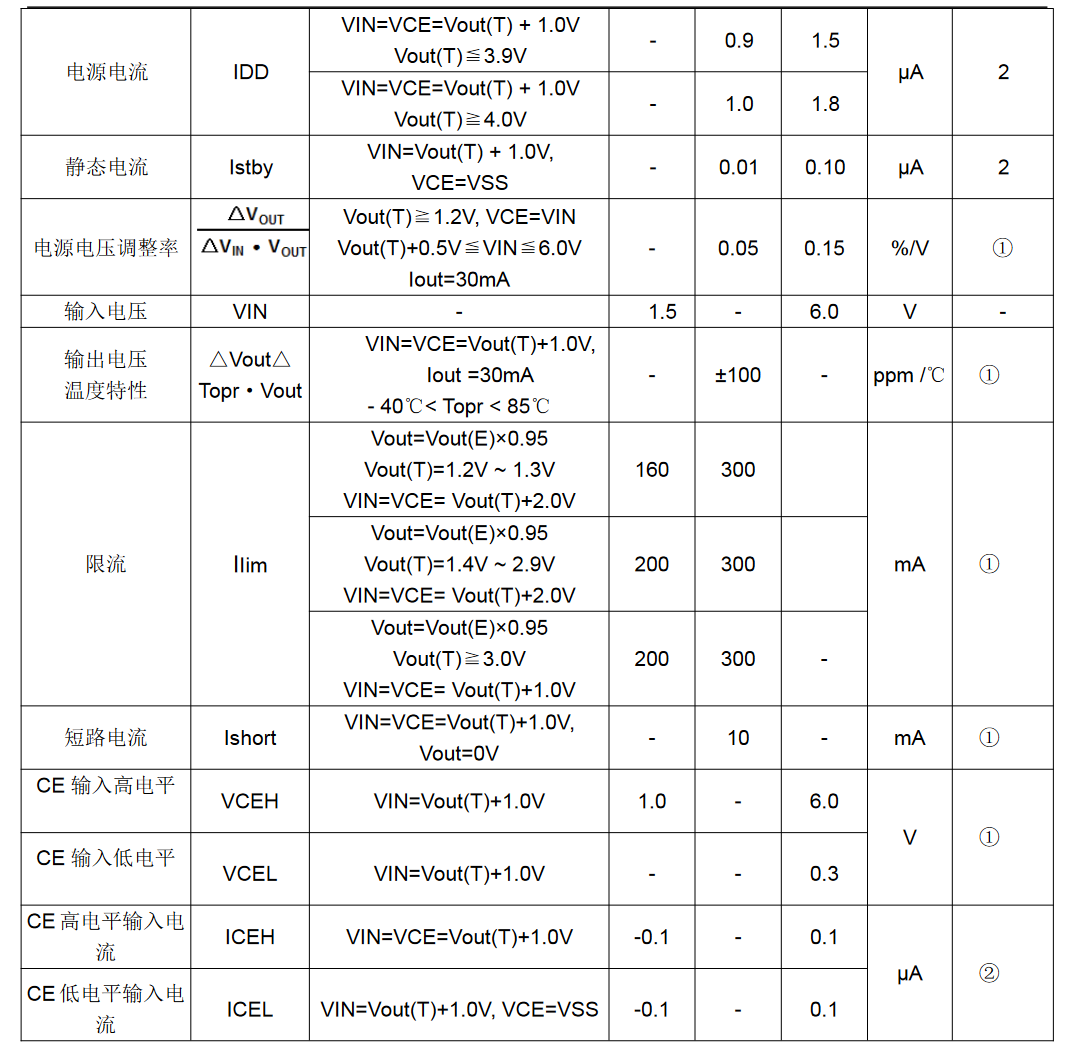
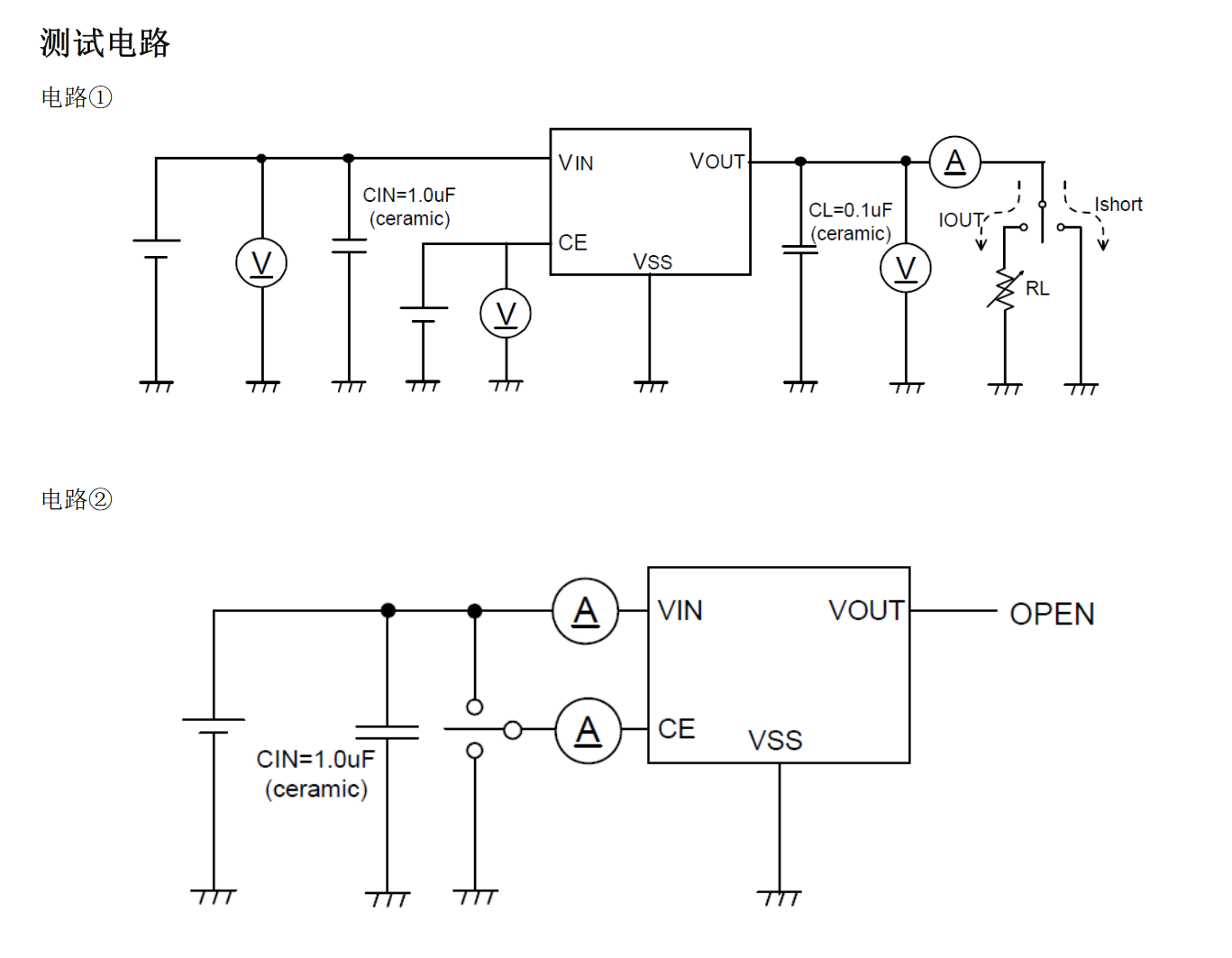
五、操作说明
短保护电路
FM6215 系列的调节器通过内置的折返式限流保护电路。当负载电流达到当前的极限水平时,限流电路开始工作,输出电压下降。由于输出电压下降,折返式限流电路控制,输出电流进一步降低。当输出销短路时,电流约为10mA。
CE 引脚
集成电路的内部电路可以通过与 FM6215B 系列的 CE 信号进行操作或关闭。在关机模式下,VOUT pin 的输出将通过内部下拉电阻下拉到 VSS 水平。FM6215 系列的“CE”使能控制电压。建议使用 VIN 或 VSS 电压。CE电平设置不合理,可能会导致集成电路内部电路的电流增加。

使用说明
1.请在规定的绝对最大额定值下使用这个 IC。如果超过额定值,IC 可能会发生故障。
2.如果布线阻抗高,操作可能变得不稳定。 噪声和/或相位滞后取决于输出电流。
3. FM6215 系列,为了稳定 VIN 的电压水平,建议 VIN 引脚和 VSS 引脚之间采用 0.1 至 1μF 输入电容(CIN)。
此外,为了防止瞬态响应引起的下冲和过冲,建议 VOUT 引脚和 VSS 引脚之间采用 0.1~1.0uF 的输出电容(CL)。
并且,请将输入电容(CIN)和输出电容(CL)尽可能靠近芯片。