信源编码与信道转移矩阵

news2024/11/17 5:23:30

一. 信息论模型

二. 点对点通信模型

三. 信源编码

四. 信道转移矩阵

4.1 二进制对称信道

4.2 二进制擦除信道

五. 小结

（1）信道直射与反射

（2）信道散射

（3）信道时变性

一. 信息论模型

1948年，Claude E. Shannon在《A mathematical theory of communication》论文中提出了信息论（information theory）。在点对点的通信中，发射方产生一个信息（比如像素的灰度值，传感器测量的物理量），接收方恢复出该信息。

信源（information source）：根据随机性产生消息；

发射机（transmitter）：产生信号；

信道（channel）：包含噪声源，比如电路的热噪声，无线信道的多径衰落；

接收机（receiver）：根据接受信号，恢复出消息；

一般提前已知信源与信道的统计特征，信息论尝试从数学的角度来解释安全传输流程。

二. 点对点通信模型

从模块化的角度来讲，物理层安全通信需要编码和解码的过程。信源编码的本质是压缩。

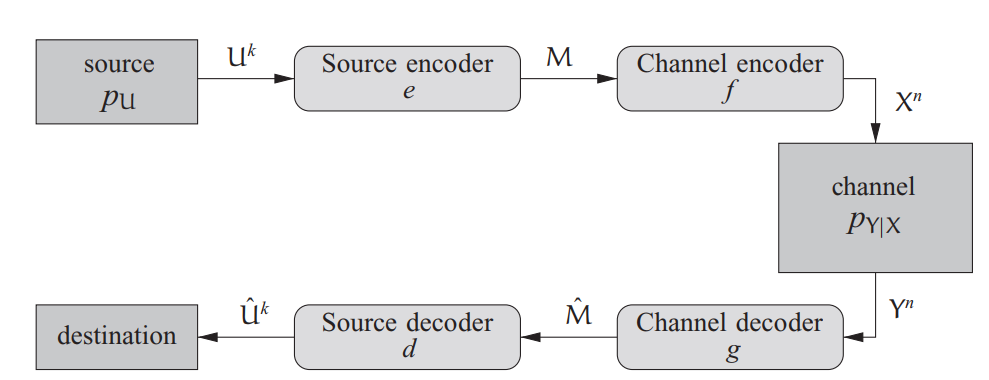
$U^k$ ：信源符号；

M：消息；

$X^n$ :信道编码结果；

$Y^n$ ：信道传输结果；

$\hat M$ ：信道解码后的消息；

$\hat U^k$ ：解码后的信源符号；

三. 信源编码

信源是离散无记忆的DMS（discrete memoryless source），代表产生的符号都是独立同分布的，写做：

$(U,P_u)$

其中U代表有限字母集（alphabet）， $P_u$ 代表概率分布，也可以把U看做随机变量。

信源编码写做 $C_k$ ，其中k代表序列长度。编码后的消息集合为：

$M=[1,2^{kR}]$

编码函数e可以将k长的信源符号 $u^k$ 编码成消息m，如下：

$e:U^k\to M$

解码函数可以将一个消息m解码成k长的信源符号，当然也可能会出现解码失误，如下：

$d:M\to U^k\cup\lbrace ?\rbrace$

输入长度为k，输出长度为kR，所以压缩率为R。考虑一般性，kR可能非整数，所以压缩率（compression rate）的一般表达形式为：

$\frac{1}{k}log\lceil 2^{kR}\rceil$

单位为bit/source symbol。

当 $\hat U^k\neq U^k$ 时，则会出现译码错误，由此可定义错误概率：

其中编码译码方案 $C_k$ 全局已知。在网络安全通信中，我们希望合法端错误概率低，窃听端错误概率高。

四. 信道转移矩阵

信道模型抽象成离散无记忆信道（discrete memoryless channel DMC），表示为：

$(X,P_{Y|X},Y)$

其中X代表输入字母集，Y代表输出字母集， $P_{Y|X}$ 代表条件概率分布，也就是X代表信道输入，Y代表信道输出。

条件概率也可以写做信道转移矩阵，如下：

$(P_{Y|X}(y|x))_{X,Y}$

4.1 二进制对称信道

二进制对称信道，binary symmetric channel，BSC

BSC(P)也属于离散无记忆信道DMC，写做：

$(\lbrace0,1\rbrace,P_{Y|X},\lbrace0,1\rbrace)$

输入为0或1，输出为0或1。转移概率为P，代表0变1的概率为P，1变0的概率为P，0变0的概率为1-P，1变1的概率为1-P。写成信道转移矩阵，如下：

4.2 二进制擦除信道

二进制擦除信道，binary erasure channel, BEC

擦除概率写做 $\epsilon\in [0,1]$ ，该信道模型为 $BEC(\epsilon)$ ，同样也属于离散无记忆信道DMC，如下：

$(\lbrace0,1\rbrace,P_{Y|X},\lbrace0,?,1\rbrace)$

0变成？的概率为 $\epsilon$ ，0变成0的概率为1- $\epsilon$ ，0变成1的概率为0

1变成？的概率为 $\epsilon$ ，1变成1的概率为1- $\epsilon$ ，1变成0的概率为0

写成信道转移矩阵如下：

五. 小结

无线信道具有互易性，时变性和空间唯一性。

典型无线信道环境中电磁波的基本传播机制如下图：

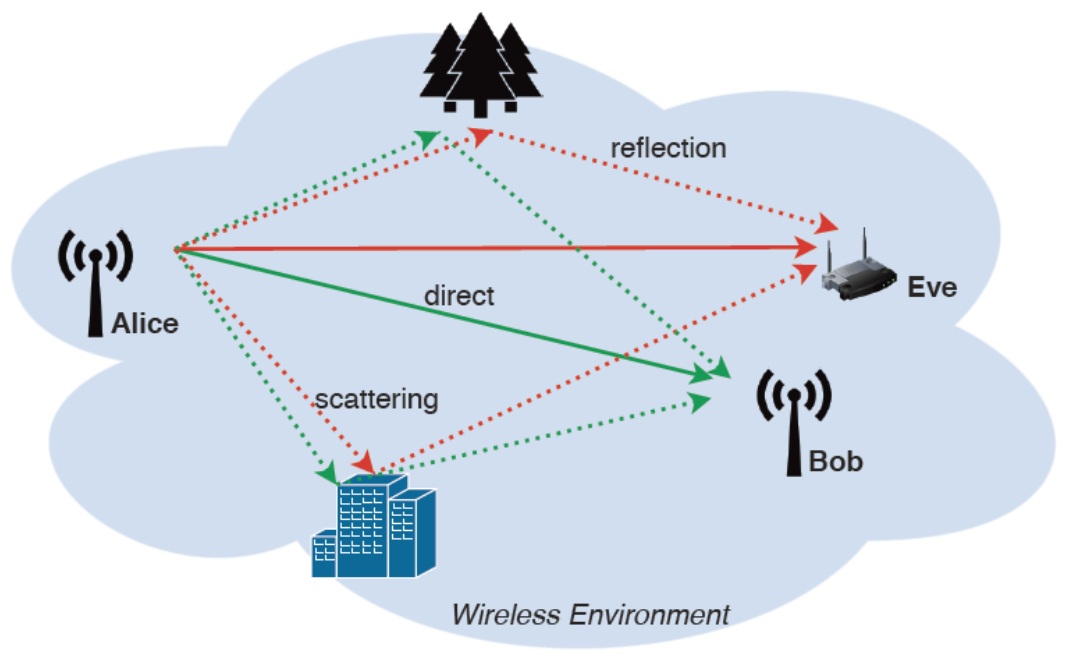
一般认为，无线通信中电波传播机制主要包括直射（direct）、反射（reflection）和散射（Scattering），有的场景还会涉及到折射、穿透等。

（1）信道直射与反射

直射传播指信号直接从发射天线到达接收天线，没有经过任何障碍物的传播方式。这种传播方式在空旷的地区效果最好，信号传输距离远，信噪比高。

反射传播指无线信号在遇到介质表面时，一部分能量被反射回去，沿原路返回，另一部分能量则继续传播的现象。这种传播方式通常发生在金属、水面、建筑物等表面。

反射信号与直射信号叠加在一起，形成多路径传播的效应。

（2）信道散射

散射传播指信号在经过物体表面或介质中微小不规则的颗粒或边缘时，发生多次反射、折射、绕射等现象，使得信号在空间中分散的传播方式。这种传播方式会造成信号的强度分布不均匀，信号失真和多径效应等问题。

另外，存在直射传播的信道被称为视距传输（Line-of-Sight， LOS），而其他传播机制的信道被称为非视距传输（Non-line of Sight， NLOS）。

（3）信道时变性

无线信道衰落可以分为大尺度衰落和小尺度衰落，又称为快衰落和慢衰落。大尺度衰落是指在信号传输的大范围距离内（一般为数百米以上），由于信号的路径损耗和阴影衰落等因素导致的信号功率变化。大尺度衰落的特点是空间相关性强，变化缓慢，可以通过减小传输距离、使用更高的天线高度、增大发送功率等方法来降低其影响。

小尺度衰落是指在信号传输的短距离范围内（一般为数十米以下），由于信号经历多条不同路径导致的信号幅度和相位的随机变化，包括多径效应和多普勒效应等。小尺度衰落的特点是空间相关性弱，变化快速，可以通过使用合适的调制技术、信号预处理、天线阵列等方法来抑制或利用其特性来提高系统性能。

小尺度衰落，时域上对应多径效应，频率域上对应多普勒频移效应引发的频率色散。若考虑多输入多输出 MIMO技术，小尺度衰落还需要考虑空域上的特性，即无线信道的空间角度扩展信息。

总的来说，大尺度衰落主要受到距离和环境的影响，而小尺度衰落主要受到多径效应和信号随机性的影响。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1363533.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！