生成式AI在自动化新时代中重塑RPA
news2026/2/8 10:46:43
核心RPA技术专注于自动化企业中常规的重复性任务。与传统的RPA不同,新一代的RPA融合了生成式AI技术,赋予自动化操作更高的灵活性和效率。
生成式对抗网络(GAN)和检索增强生成(RAG)这样的生成式AI技术,已经证明了其在创造逼真图像和提供上下文相关信息方面的强大能力。将生成式AI整合进RPA框架,能够为自动化流程带来以下多维度的机遇:
在银行业中,贷款审批流程是核心业务环节之一。这一流程传统上依赖于大规模的数据收集和基于规则的决策模式。在这一背景下,RPA能够高效处理标准化流程。它开始于从新的贷款申请中提取关键信息,包括申请人的个人资料、职业状态、信用评分及就业记录等。接着,RPA工具会按照既定的贷款准则对这些信息进行核查,并依据预设的商业规则做出初步决策。
在医疗保健行业,RPA和生成式AI的应用正在深度重塑流程自动化的格局,尤其在患者诊断这一关键环节体现尤为显著。RPA在医疗领域扮演着基础性角色,其职能范畴包括从提取患者历史病例、实验室测试结果到药品信息的整合,以及处理第三方授权和患者入院手续等环节。
在最新科技潮流面前,公司的CIO和CRO可能会感到充满挑战,他们必须在创新与保护既有投资之间找到平衡点。
这涉及审视现有的工作流程,以识别那些适宜借助人工智能进行人机协作和处理复杂决策的领域。评估支持人工智能所需的基础设施和资源,考虑数据的准备和标注要求,确保获取高质量且多样化的数据集以便于人工智能做出有效的决策,并与专业的人工智能解决方案供应商和专家合作,确保技术能够与业务需求相匹配。
构建一个对人工智能及其他新技术持续学习的企业文化。提供全面的关于人工智能应用、决策解释及反馈机制的培训,鼓励人工智能专家与员工之间的协作,并获得实际操作的经验。
初始时,通过试点项目评估人工智能的有效性,之后再逐步扩展规模。持续监控由人工智能增强的流程,并设立明确的成功评价标准。同时,确保人工智能的应用遵循法律和伦理标准,以及准备管理由人工智能集成带来的组织变革。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1363524.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Blazor项目如何调用js文件
以下是来自千问的回答并加以整理:(说一句,文心3.5所给的回答不完善,根本运行不起来,4.0等有钱了试试)
在Blazor项目中引用JavaScript文件(.js)以实现与JavaScript的互操作ÿ…
GAMES101:作业6记录
1 总览
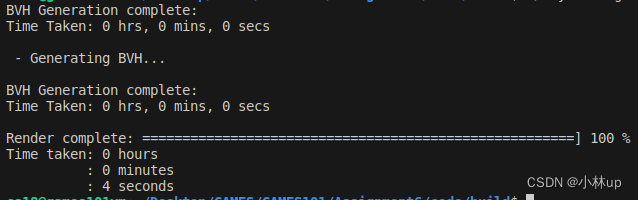
在之前的编程练习中,我们实现了基础的光线追踪算法,具体而言是光线传输、光线与三角形求交。我们采用了这样的方法寻找光线与场景的交点:遍历场景中的所有物体,判断光线是否与它相交。在场景中的物体数量不大时,该做法可以取得良好的结果,但当物体数量增多、模型变得更…
前端JS加密对抗由浅入深-1
前言:
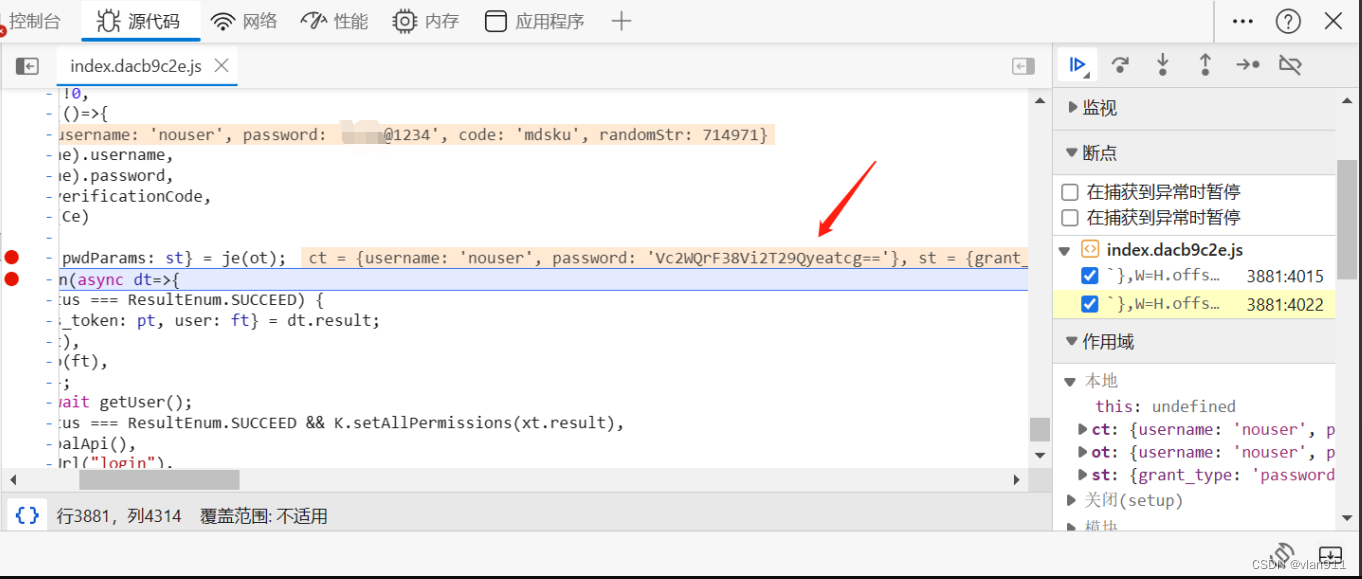
本文主要讲解,针对前端加密数据传输站点,如何进行动态调试以获取加密算法、秘钥,本次实验不涉及漏洞挖掘,仅为学习演示,环境为本地搭建环境
此次站点加密方式为AES加密方式,现如今越来越…
【STM32】STM32学习笔记-DMA直接存储器存储(23)
00. 目录 文章目录 00. 目录01. DMA简介02. DMA主要特性03. 存储器映像04. DMA框图05. DMA基本结构06. DMA请求07. 数据宽度与对齐08. 数据转运DMA09. ADC扫描模式DMA10. 附录 01. DMA简介
小容量产品是指闪存存储器容量在16K至32K字节之间的STM32F101xx、STM32F102xx和STM32F…
Mybatis-Mapper代理开发
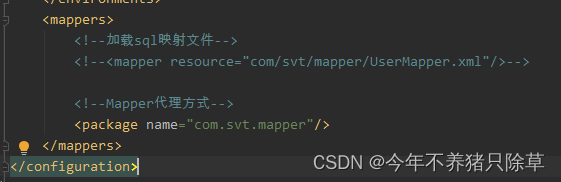
Mapper代理开发 目的使用Mapper代理方式入门1.定义与SQL映射文件同名的Mapper接口,并且将Mapper接口和SQL映射文件放置在同一目录下首先新建一个Mapper接口编译mybatis-demo更改sql映射文件路径 2.设置SQL映射文件的namespace属性为Mapper接口全限定名3.在Mapper 接…
论文浅尝 | 以词-词关系进行分类的统一命名实体识别
笔记整理:曹旭东,东南大学硕士,研究方向为知识图谱构建、自然语言处理 链接:https://arxiv.org/abs/2112.10070 1. 动机 在以前的工作中,命名实体识别(NER)涉及的主要问题有三种类型,…
Java数据结构:1. 数据结构前置知识
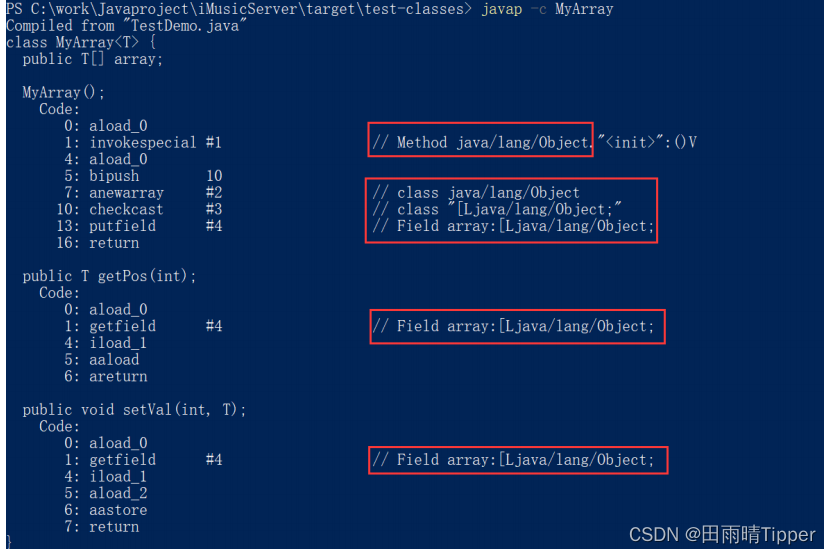
文章目录 一、初识数据结构二、初识集合框架1. 什么是集合框架2. 集合框架的重要性3. 背后所涉及的数据结构以及算法 三、时间复杂度空间复杂度1. 算法效率2. 时间复杂度(1)概念(2)大O的渐进表示法(3)推导大…
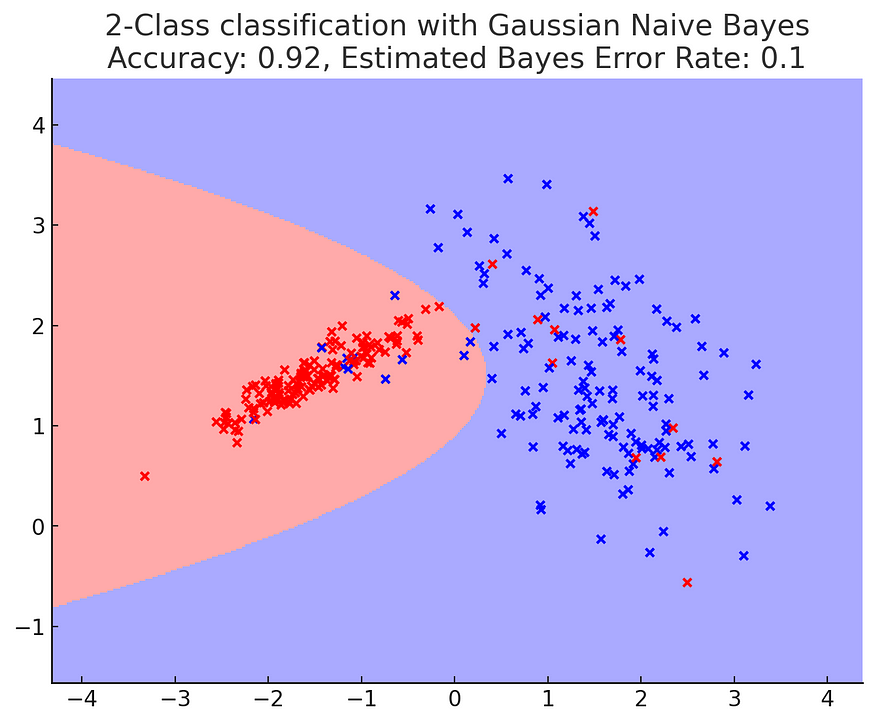
了解统计分类中的贝叶斯理论误差限
一、介绍 统计分类和机器学习领域正在不断发展,努力提高预测模型的准确性和效率。这些进步的核心在于一个基本基准,即贝叶斯理论误差极限。这个概念深深植根于概率和统计学,是理解分类算法的局限性和潜力的基石。本文深入探讨了贝叶斯错误率的…
Java技术栈 —— Hadoop入门(一)
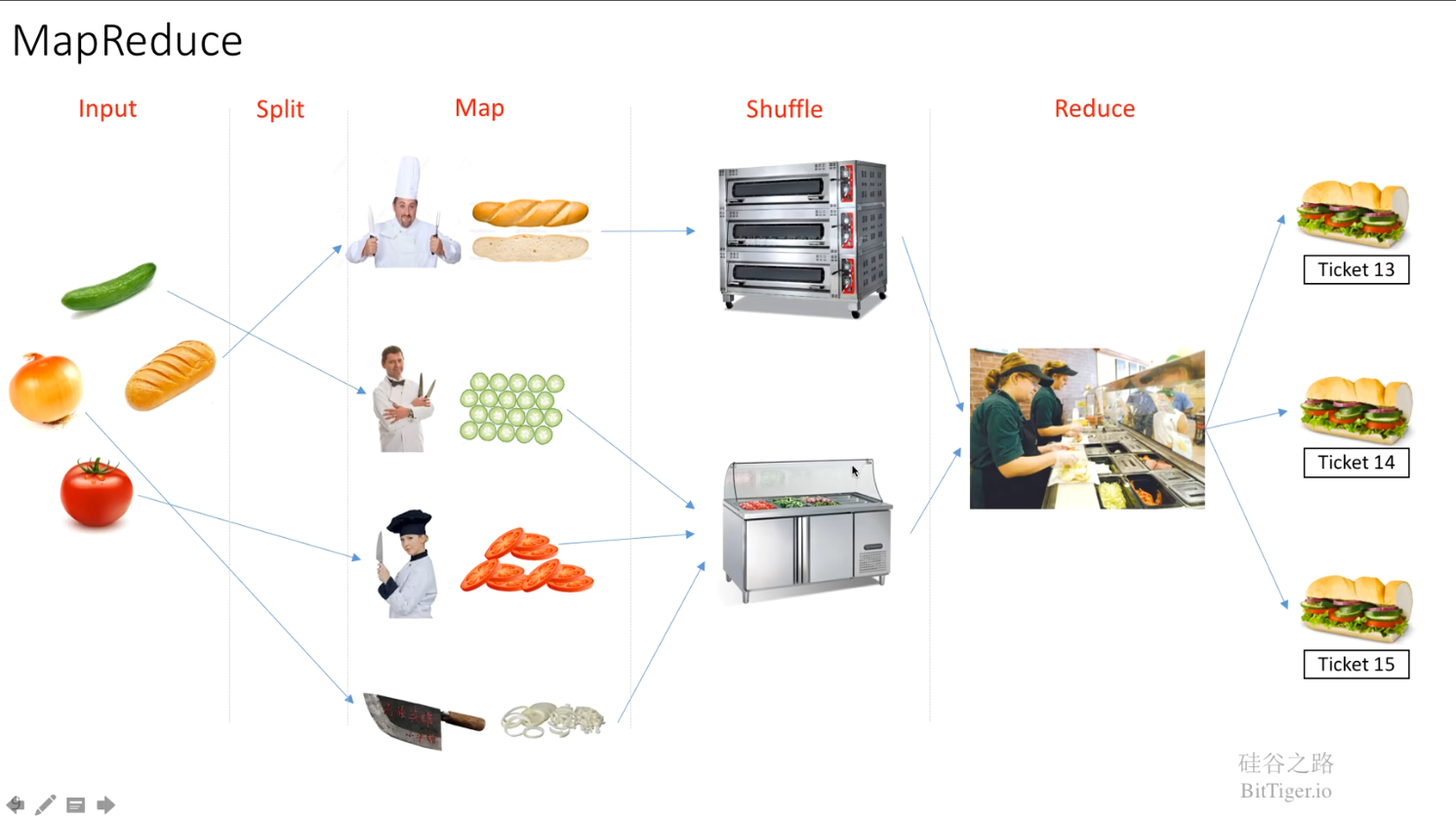
Java技术栈 —— Hadoop入门(一) 一、Hadoop第一印象二、安装Hadoop三、Hadoop解析3.1 Hadoop生态介绍3.1.1 MapReduce - 核心组件3.1.2 HDFS - 核心组件3.1.3 YARN - 核心组件3.1.4 其它组件3.1.4.1 HBase3.1.4.2 Hive3.1.4.3 Spark 一、Hadoop第一印象…
用通俗易懂的方式讲解:万字长文带你入门大模型
告别2023,迎接2024。大模型技术已成为业界关注焦点,你是否也渴望掌握这一领域却又不知从何学起?
本篇文章将特别针对入门新手,以浅显易懂的方式梳理大模型的发展历程、核心网络结构以及数据微调等关键技术。
如果你在阅读中收获…
NJIT数据结构期末复习
任何时候学习都不算晚,保持终身学习!!!
数据结构期末复习
第一章 1.以下程序段的时间复杂是多少? int sum 0; for(i1;i<n;i) { for(j1;j<n;j) { sum; } }
答:O(n^2)
第二章 2.遍历单链表&…
【计算机组成原理】总复习笔记(上)
特别声明: 本文仅供参考,本文部分内容来自AI总结、网络搜集与个人实践。如果任何信息存在错误,欢迎读者批评指正。本文仅用于学习交流,不用作任何商业用途。 文章目录 第 1 章 计算机系统概述1.1 冯诺依曼计算机结构1.2 高级语言与机器级目标代码1.3 计算…
【AI】搭建Windows Linux子系统(WSL2)CUDA环境
0.准备工作
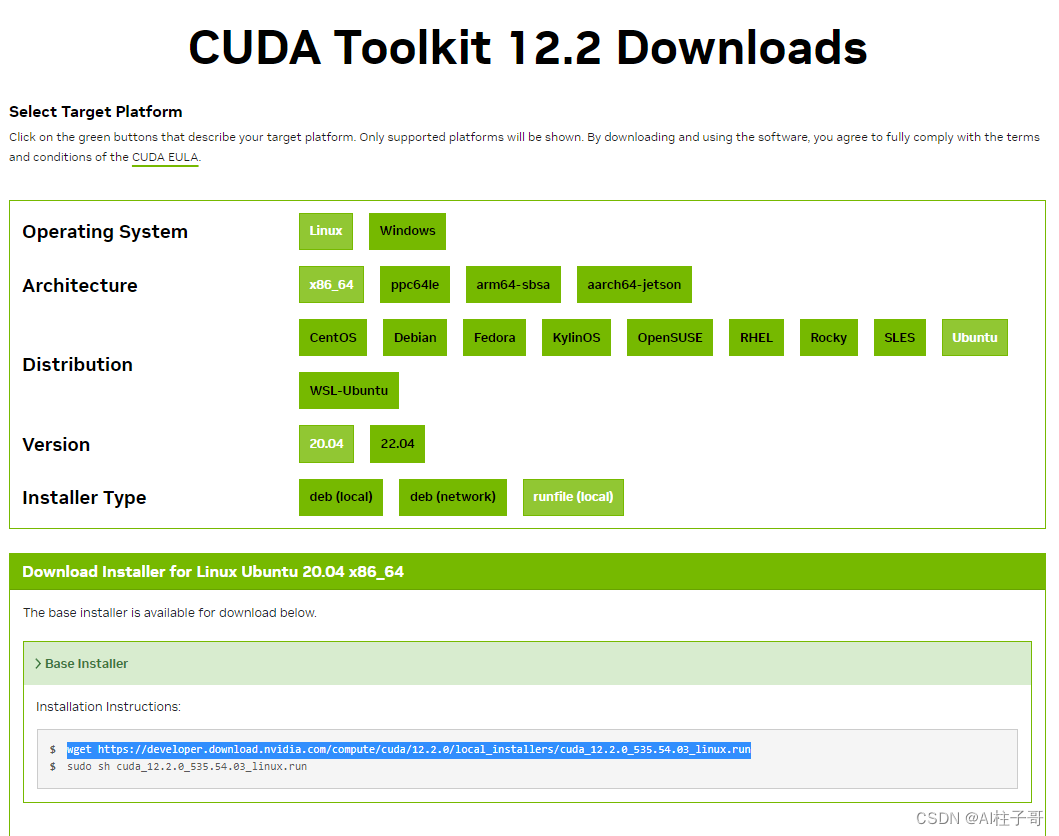
Windows本机安装CUDA Driver 首先去下载页面下载驱动文件
点击Get CUDA Driver进入下载页面,我看下载页面跟普通驱动下载页面相同,感觉应该不是单独的驱动,只要之前显卡已经安装好了CUDA的驱动,就可以先省略这一步。…
使用 CMake 和 Ninja 构建 C/C++ 项目的教程
使用 CMake 和 Ninja 构建 C/C 项目的教程
CMake 是一个跨平台的开源构建工具,它简化了项目的构建过程。而 Ninja 是一个快速、轻量级的构建系统,与 CMake 配合使用可以提高项目的构建效率。本教程将向你介绍如何使用 CMake 和 Ninja 来构建你的 C/C 项…
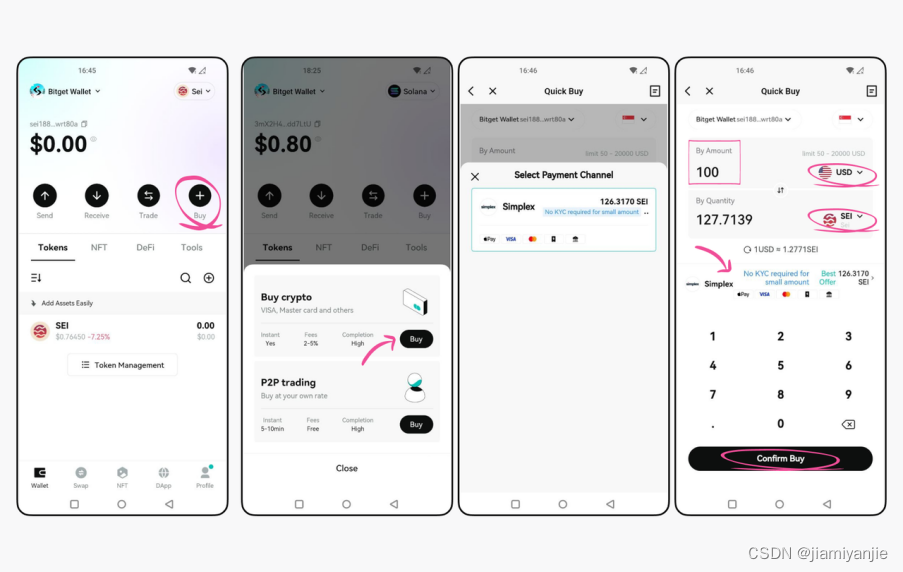
一文了解 DeFi 原生公链 Sei,以及钱包添加教程什么是Sei?
Sei,领先Layer 1公链,专攻加密资产交易。不局限于DeFi,还进军游戏、社交媒体和NFTs等领域,构建了多功能区块链生态系统。在众多公链中,Sei凭借卓越处理速度和技术创新崭露头角。独特共识机制和技术创新功不可没。作为通…
【LeetCode每日一题】2807. 在链表中插入最大公约数(模拟+求最大公约数的6中写法)
2024-1-6 文章目录 [2807. 在链表中插入最大公约数](https://leetcode.cn/problems/insert-greatest-common-divisors-in-linked-list/)思路:模拟求最大公约数的几种方法: 1.暴力枚举法2.辗转相除法3.辗转相除法 ---递归调用4.辗转相除法 ---递归调用---…
摄像头视频录制程序使用教程(Win10)
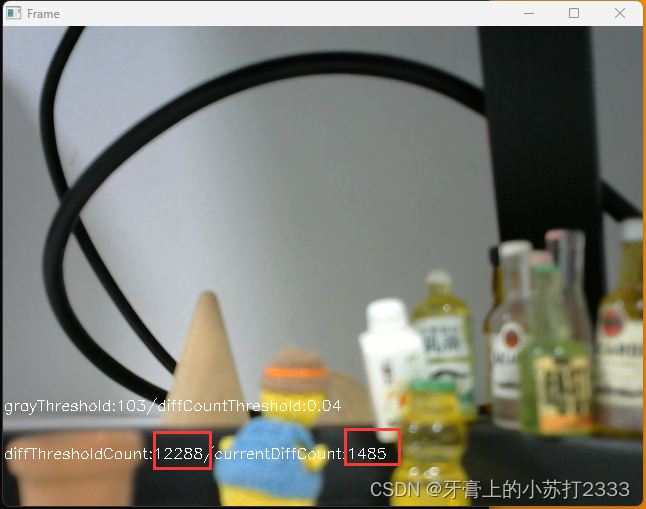
摄像头视频录制程序-Win10 🥗介绍🍛使用说明🚩config.json 说明🚩启动🚩关闭🚩什么时候开始录制?🚩什么时候触发录制?🚩调参 🥗介绍
检测画面变化…
每日一练:LeeCode-388. 文件的最长绝对路径【字符串、栈方法】
本文是力扣LeeCode-388. 文件的最长绝对路径 学习与理解过程,本文仅做学习之用,对本题感兴趣的小伙伴可以出门左拐LeeCode。
假设有一个同时存储文件和目录的文件系统。下图展示了文件系统的一个示例:
这里将 dir 作为根目录中的唯一目录。…