任何时候学习都不算晚，保持终身学习！！！

数据结构期末复习

第一章
1.以下程序段的时间复杂是多少？
int sum = 0;
for(i=1;i<=n;i++) {
for(j=1;j<=n;j++) {
sum++;
}
}

答：O(n^2)

第二章
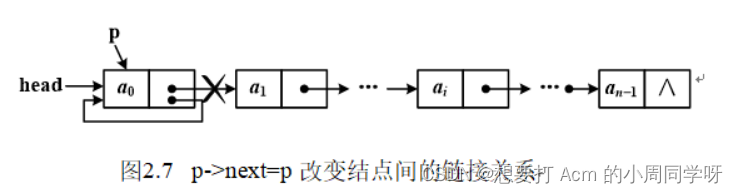
2.遍历单链表，如果将p=p.next语句写成p.next=p，结果会怎样？画出示意图。

答：语句p=p.next使p移动到后继结点，此时结点间的链接关系没有改变。如果写成p.next=p，则使p.next指向p结点自己，改变了结点间的链接关系，并丢失后继结点，如图示，遍历算法也变成死循环。

3.设front指针指向非空单链表中的某个结点，在front结点之后插入q结点，执行以下语句结果会怎样？画出示意图。
Node q = new Node(x);
Front.next = q; //①
q.next = front.next; //②

答：②句相当于q.next = q;，产生错误，结点间的链接关系如图2.8所示。

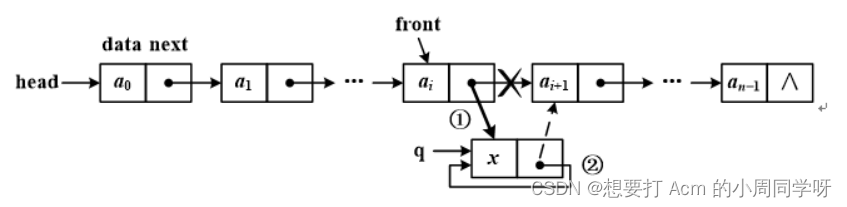
错误原因：上述后两条语句次序颠倒。对front.next赋值将改变结点间的链接关系，从而丢失后继结点地址。因此，在改变结点链接关系时，应该先获得front.next的值，再对其赋值。头插入存在同样问题。

4.能否使用以下语句创建循环单链表的头结点？为什么？
head = new Node(NULL, head);
答：不能。因为申请结点存储空间时head没有初始化，实际语义需要的是将该结点地址作为其next域值，做不到。

5.在长度为n的顺序表中插入第i个元素(0≤i≤n)，要移动_________个元素。
答：n-i

6.设指针p指向单链表中的某个结点（非两端），则删除p结点的后继结点的语句为________________________________________________________________。
答：p.next=p.next.next;

7.设p指向双链表的某个结点，在p结点之前插入一个值为x的结点，语句如下：
DoubleNode q = new DoubleNode(x, p.prev, p);
p.prev = q;
p.prev.next = q;

答：
后两句语句次序反了，导致错误。
改正：改变后两句语句次序。
DoubleNode q = new DoubleNode(x, p.prev, p);
p.prev.next = q;
p.prev = q;

8.以下函数功能是什么？算法效率如何？如何改进，使遍历单链表时间复杂度是O(n)？
int min(SinglyList list)
{
if (list.isEmpty())
throw new Exception(“单链表为空，不能计算。”);
int minvalue=list.get(0);
for (int i=0; i<list.length(); i++)
if (minvalue>list.get(i))
minvalue = list.get(i);
return minvalue;
}

答：
① 功能是返回单链表的最小值。
② 由于list.length()和list.get(i)时间复杂度是O(n)，遍历单链表的时间复杂度则是 ，效率很低，不可接受。
③ 改进，……，遍历单链表时间复杂度是O(n)。

9.遍历单链表，如果将p=p.next语句写成p.next=p，结果会怎样？画出示意图

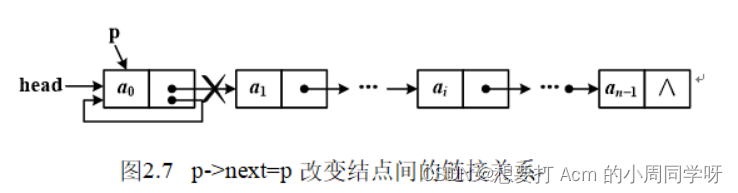
答：语句p=p.next使p移动到后继结点，此时结点间的链接关系没有改变。如果写成p.next=p，则使p.next指向p结点自己，改变了结点间的链接关系，并丢失后继结点，如图2.7所示，遍历算法也变成死循环。

10.设front指针指向非空单链表中的某个结点，在front结点之后插入q结点，执行以下语句结果会怎样？画出示意图。
Node q = new Node(x);
front.next = q; //①
q.next = front.next; //②

答：
②句相当于q.next = q;，产生错误，结点间的链接关系如图所示。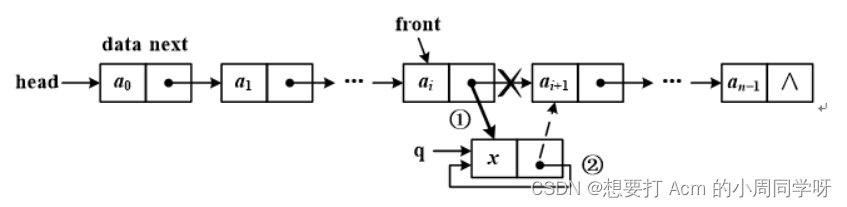

错误原因：上述后两条语句次序颠倒。对front.next赋值将改变结点间的链接关系，从而丢失后继结点地址。因此，在改变结点链接关系时，应该先获得front.next的值，再对其赋值。头插入存在同样问题。

11.能否使用以下语句创建循环单链表的头结点？为什么？
head = new Node(NULL, head);
答：不能。因为申请结点存储空间时head没有初始化，实际语义需要的是将该结点地址作为其next域值，做不到。

第三章
12."“和” “有什么差别？
答：”“是空串，长度为0；” "是空格串

13.串的存储结构有几种？串通常采用什么存储结构？
答：串可采用顺序存储结构和链式存储结构，串通常采用顺序存储结构。

14.已知target=“aaabaaab”、pattern=“aaaa”，画出采用Brute-Force算法的模式匹配过程，给出比较结果、子串匹配次数和字符比较次数。

答：
比较结果：匹配不成功，匹配子串位置为-1；子串匹配5次，字符比较14次。

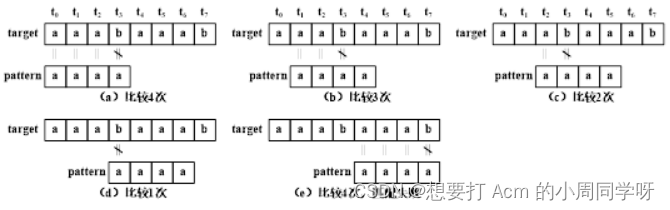
模式串"aaaa"的Brute-Force算法模式匹配过程

15.以下算法在什么情况会出现怎样的错误？举例说明。怎样改正？
//将串中所有与pattern匹配的子串替换为str
void replaceAll(MyString pattern, MyString str)
{
int start=search(pattern);
while (start!=-1)
{
remove(start, pattern.n);
insert(start, str);
start = search(pattern, start);
}
}

“abbcdf”
pattern=”a”
str=”ab”
start = 0
start = 0
答：
若欲将"a"替换为"ab"，上述函数会将作为替换串"ab"中的"a"再次进行替换，导致死循环。将循环体中第3句改为如下，从替换子串的下一个字符开始再次查找匹配子串。
start = search(pattern, start+str.n); //从替换子串的下一个字符开始再次查找匹配子串

16.已知target=“abcababcabababcababc”，pattern=“ababcababc”，求模式串改进的next数组，画出KMP算法模式匹配过程，给出比较结果，以及子串匹配次数和字符比较次数。
本题目的：理解改进next数组的next[j]=next[k]。
答：

第四章
17.(A+B)*(C-D)/E的后缀表达式为_________________________________________。
答：AB+CD-*E/

18.已知一个顺序循环队列容量为100，设front=99，若rear=99，表示队列空；若rear=98___，表示队列满。
答：99；98
顺序循环队列空的条件：front == rear
队列满的条件： front=(rear+1)%length,rear=99,front=0
入队操作：rear =(rear+1)%length
出队操作：front=(front+1)%length

19.设一个顺序循环队列的数组容量为length，front和rear分别是队首和队尾下标，判断队列满的条件是___________________________________________________________。
答：front==(rear + 1)% length

20.将顺序存储结构的队列设计成循环结构的理由是_______________________________。
答：避免出现“假溢出”情况。

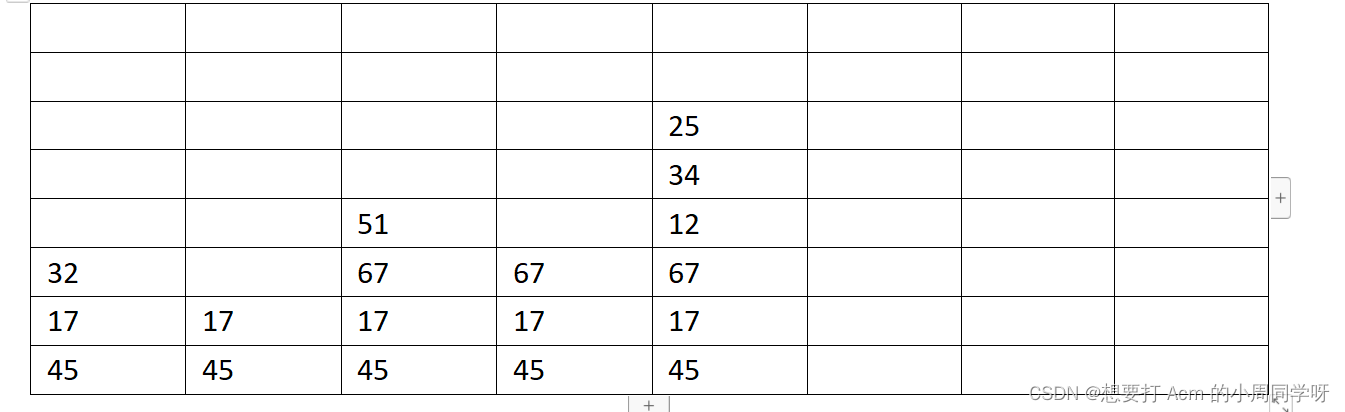
21.什么是栈？栈有何特点？画出以下序列执行以下操作的顺序栈示意图，标明栈顶位置。{45,17,32,67,51,74,12,92,34,25}，{入, 入, 入, 出, 入, 入, 出, 入, 出, 入, 入, 出, 入, 入}

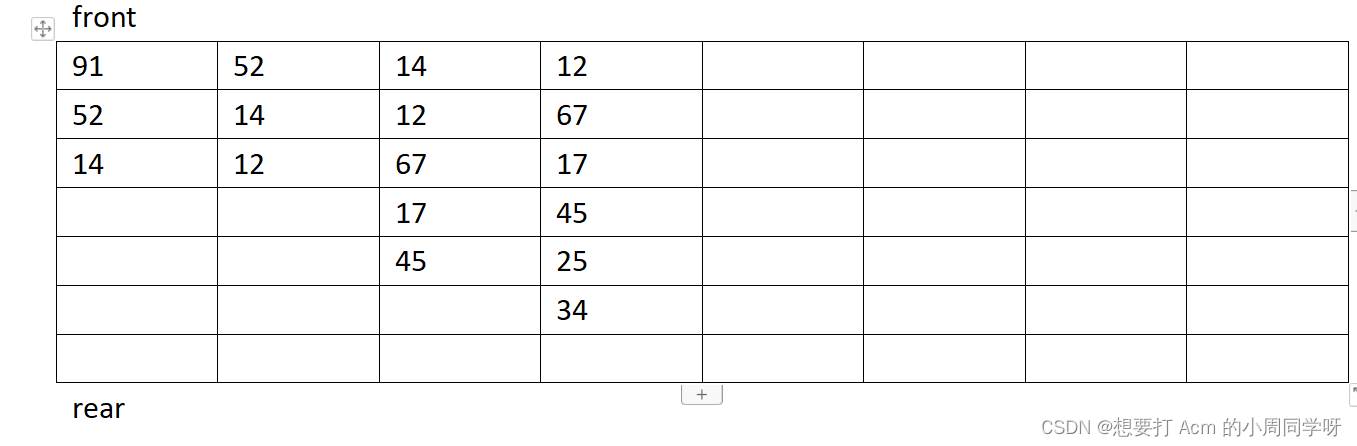
22.什么是队列？队列有何特点？画出以下序列执行以下操作的链式队列示意图，标明队列首尾位置，说明队列空和队列满条件。{91,52,14,12,67,17,45,25,34}，{进,进,进,出,进,出,进,进,进,出,进,进}
答：队列的插入和删除操作分别在线性表的两端进行，队列的特点是“先进先出”。

23.有个莲花池里起初有一只莲花，每过一天莲花的数量就会翻一倍。假设莲花永远不凋谢，30天的时候莲花池全部长满了莲花，请问第23天的莲花占莲花池的几分之几？请实现递归函数代码。
答：
底层实现.栈
栈遍历二叉树 . 模拟了递归
首先定义最终终止条件f(30)=1;
然后定义递归公式中f(n)=f(n+1)0.5。
Int i=1;
F()
{
Cout<i++;
F()
}
1）边界条件
2）表达式，通式，fn=2 f(n-1)
If(边界条件)
{
Return
}
Else
{
递归公式.递归函数的调用
}
1 public class Test {
2 public static double f(double x){
3 if(x==30){
4 return 1;
5 }else{
6 return f(x+1)*0.5;
7 }
8 }
9 public static void main(String[] args) {
10 System.out.println(f(23));
11 }
12
13 }
结果：0.0078125

第五章
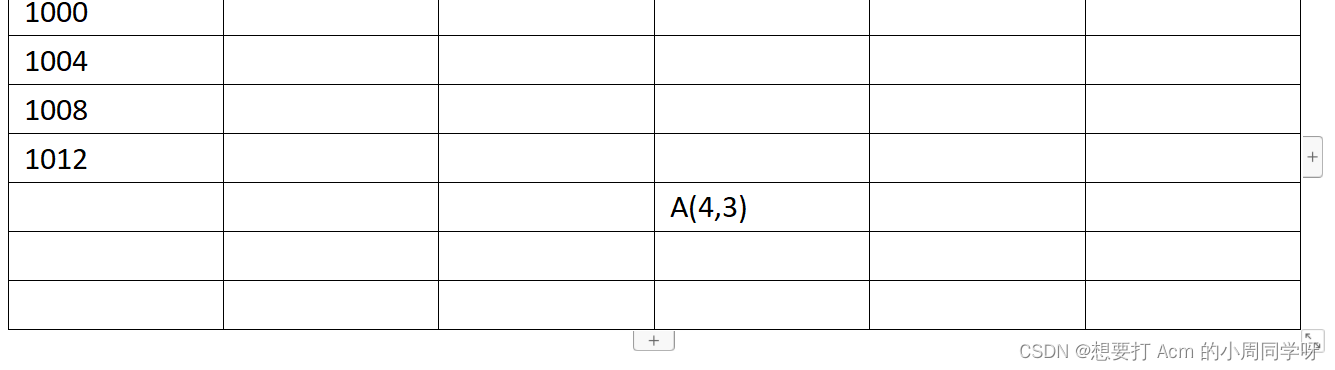
24.已知二维数组a[7][6]采用行主序存储，数组首地址是1000，每个元素占用4字节，则数组元素a[4][3]的存储地址是_____________________。
答：mat+(i*n+j)4=1000+(46+3)4=1108
Mat+(jm+i)4=1000+(37+4)*4

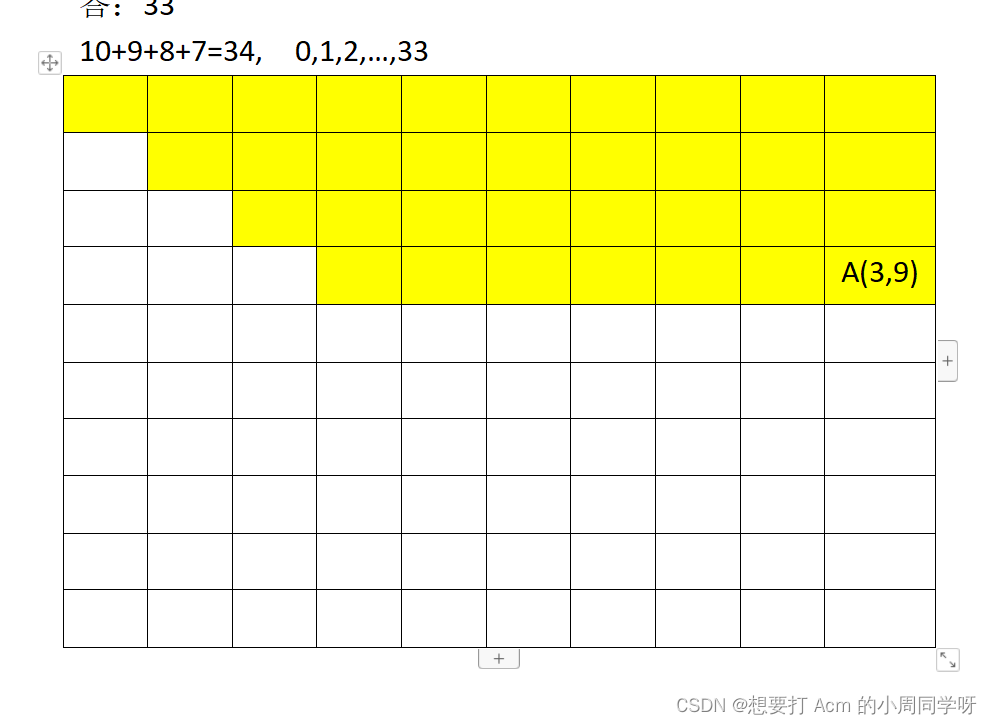
25.设A10是一个对称矩阵，将A的对角线及对角线上方的元素aij(0<=i,j<n,i<j)以行为主次序存放在一维数组中，则元素a3,9在数组中的下标（≥0）是33
答：33
10+9+8+7=34, 0,1,2,…,33

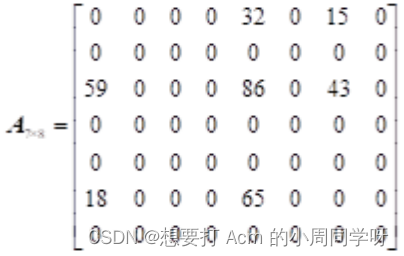
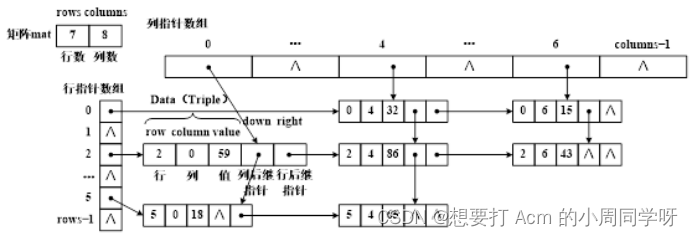
26.分别画出以下稀疏矩阵非零元素三元组的顺序表、行单链表、列单链表和十字链表的存储结构。

答：

27.计算下列广义表的长度和深度，并画出广义表双链存储结构。
中国（北京，上海，江苏（南京，苏州），浙江（杭州），广东（广州））

第六章
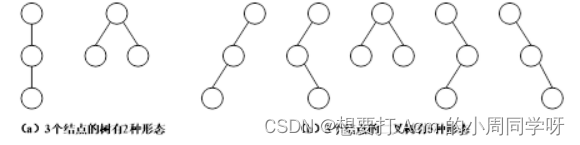
28.回答以下问题，说明二叉树与树的区别。
① 二叉树是不是度为2的树？二叉树是不是度为2的有序树？为什么？
② 画出3个结点的树和二叉树的基本形态。

答：
① 不是。二叉树与树，定义不同，二叉树有左、右子树之分。详见教材第149～150页图6.7。
② 3个结点的树有2种形态，3个结点的二叉树有5种形态，如图6.1所示。

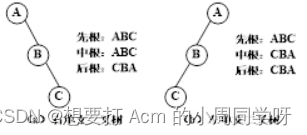
③ 先根次序遍历序列和后根次序遍历序列相同是，空树或仅有一个结点的二叉树。

29. 已知一棵二叉树的中根和后根遍历序列如下，画出据此构造的二叉树。
    中根遍历序列：C D B E G A H F I J K；
    后根遍历序列：D C E G B F H K J I A

左子树
中：C D B E G
后：D C E G B

B左
中：C D
后：D C
B右：
中：EG
后：EG

右子树:
中：H F I J K
后：F H K J I

答：

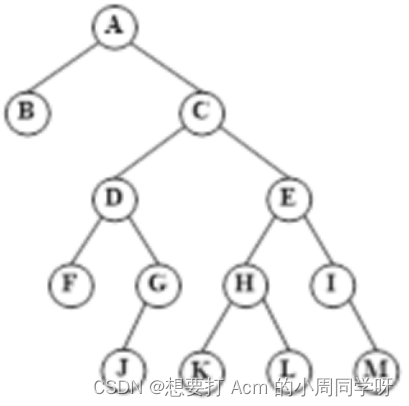
30.画出用以下广义表形式表示的一棵二叉树。
A(B,C(D(F,G(J,^{)),E(H(K,L),I(},M))))
答：

31.实现BinaryTree类声明的以下基于遍历的操作，采用合适的次序遍历。
public int count() //返回二叉树的结点数
public int height() //返回二叉树的高度
preorder();
preorder(BinaryNode p)
{
If(p==null) return;
Cout<<p.data;
Preorder(p.left)
Preorder(p.right)
}

答：
int count() //返回二叉树的结点数
{ return this.count(this.root);
}
int count(BinaryNode p) //返回以p结点为根子树的结点数，先根次序遍历
{
if (p==NULL)
return 0;
return 1+count(p.left)+count(p.right);
}

int height() //返回二叉树的高度
{
return this.height(this.root);
}
int height(BinaryNode p) //返回以p结点为根的子树高度，后根次序遍历
{
if (p==NULL)
return 0;
int lh = height(p.left); //返回左子树的高度
int rh = height(p.right); //返回右子树的高度
return (lh>=rh) ? lh+1 : rh+1; //当前子树高度=较高子树高度+1
}

32.实现BinaryTree二叉树类的拷贝构造函数。
答：
BinaryTree (BinaryTree bitree) //深拷贝构造函数，由bitree构造
{
this.root = copy(bitree.root);
}
//复制以p根的子二叉树，返回新建子树的根结点。先根次序遍历和构造算法
BinaryNode copy(BinaryNode p)
{
if (p==NULL)
return NULL;
BinaryNode q=new BinaryNode(p.data); //拷贝根节点
q.left = copy(p.left); //递归拷贝左子树
q.right = copy(p.right); //递归拷贝右子树
return q;
}

33.已知一棵完全二叉树的层次遍历序列为LKJIHGFEDCBA，则K在中根次序下的后继结点是____________________，A在后根次序下的前驱结点是_____________________。
答：C，K

34.由n个权值构造的一棵Huffman树共有______________结点，因为________________________________________________。
答：2n-1, Huffman树中没有度为1的节点，且n0=n2+1
N总=n0+n2=n0+n0-1=2n-1

35.程序阅读题：
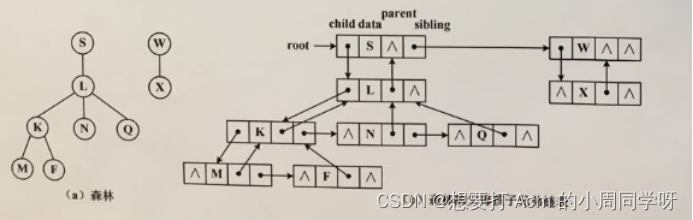
已知Tree类表示父母孩子兄弟链表存储的树，声明以下成员函数：
TreeNode insertRoot(T x) //插入x元素作为根结点，原根结点作为x的孩子，返回插入结点
TreeNode insertLastChild(TreeNode p, T x) //插入x作为p结点的最后一个孩子
TreeNode insertLastSibling(TreeNode p, T x) //插入x作为p结点的最后一个兄弟结点
TreeNode insertChild(TreeNode p, T x, int i) //插入x元素作为p结点的第i个孩子结点
阅读以下程序，画出所构造的树及其存储结构图。
void make3_3A(Tree tree)
{
tree.root = new TreeNode(‘L’);
TreeNode p=tree.insertLastChild(tree.root, ‘N’);
p=tree.insertChild(tree.root, ‘K’, 0);
tree.insertLastSibling(p, ‘Q’);
tree.insertLastChild(p, ‘M’);
tree.insertChild(p, ‘F’,1);
tree.insertRoot(‘S’);
p=tree.insertLastSibling(tree.root, ‘W’);
tree.insertLastChild(p, ‘X’);
}

答：

36.已知一棵BinaryTree二叉树采用二叉链表存储，每个结点表示一位学生某门课程成绩，结点数值范围为0～100；实现以下声明的函数，按优、良、中、及格、不及格五个等级统计人数，要求一次遍历操作效率，递归算法。
void printGrade(BinaryTree bitree) //统计bitree二叉树，输出结果
void grade(BinaryNode p, int result[]) //统计以p为根的子树，结果存入result数组，递归算法

答：

递归中共享信息
1）传参
2）全局变量

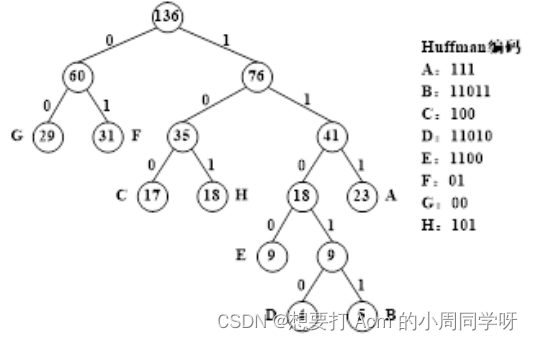
37.设一段正文由字符集{A,B,C,D,E,F,G,H}组成，其中每个字符在正文中的出现次数依次为{23,5,17,4,9,31,29,18}，采用Huffman编码对这段正文进行压缩存储，画出所构造的Huffman树，并写出每个字符的Huffman编码。
答:

第七章
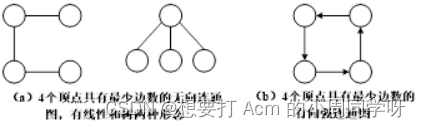
38.n个顶点具有最少边数的无向连通图和有向强连通图是怎样的？
答：

39.画出以下带权无向图的邻接矩阵表示和邻接表表示；再画出删除中顶点D后的邻接矩阵表示和邻接表表示。

答：

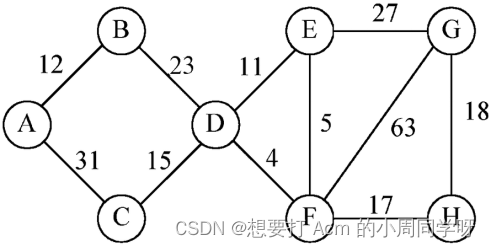
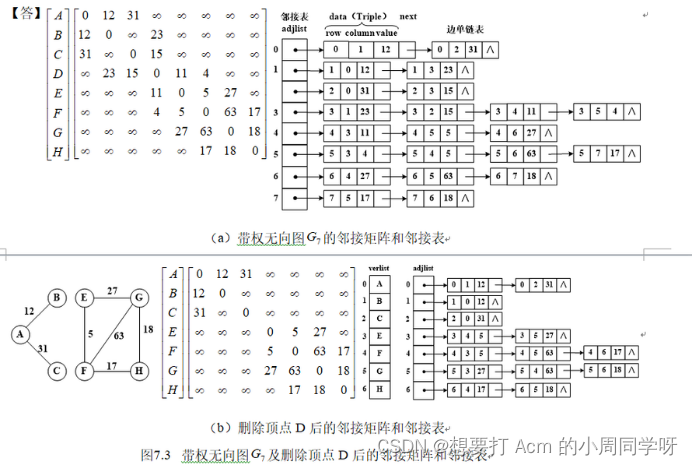
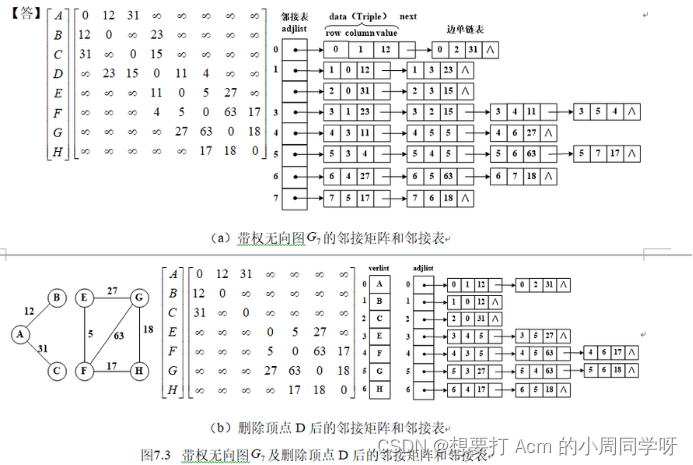
40.构造带权无向图的最小生成树，并给出该最小生成树的代价。

dda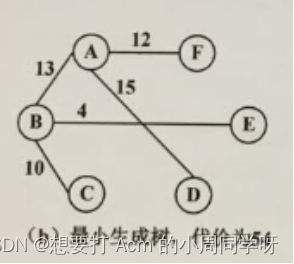41.图中顶点D的出度是_______；所有顶点的入度之和是_______。 从F到B的最短路径是________________________，路径长度是_________。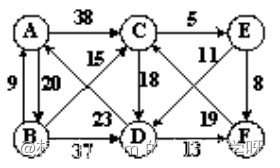

答：2，12。
（F,C,E,D,A,B），78

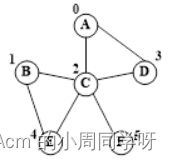
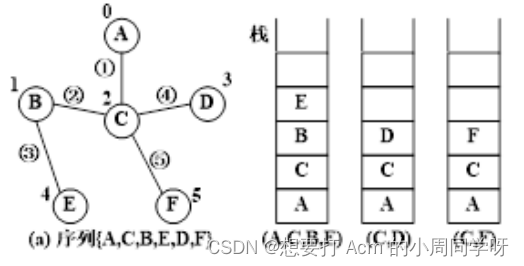
42.已知一个图及其顶点的存储次序如下，从顶点B开始进行一次深度优先搜索遍历，写出遍历序列；画出所选择的边及次序；画出栈的动态变化图，遍历一条最长路径时画一个栈，可包含多次入栈。

答：

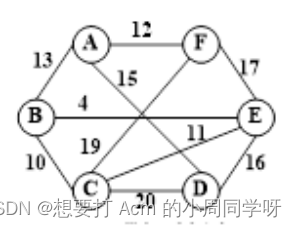
43. 构造以下带权无向图的最小生成树，并给出最小代价。

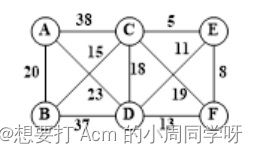
答：

最小代价59

44. 画出以下带权图顶点A的单源最短路径所选择的边，写出各路径及其长度。
45. 

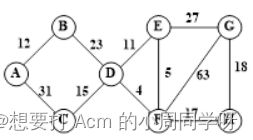
答：

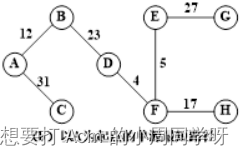
A的单源最短路径：(A,B)长度12，(A,C)长度31，(A,B,D)长度35，(A,B,D,F,E)长度44，(A,B,D,F)长度39，(A,B,D,F,E,G)长度71，(A,B,D,F,H)长度56。

第八章
45.已知关键字序列为{10,20,30,40,50,60,70,80,90}，采用二分法查找算法，给定值为90、35时分别与哪些元素比较？画出相应的二叉判定树，计算ASL（成功）、ASL（不成功）
答：

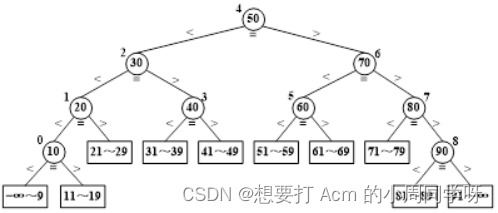
查找90比较元素是50、70、80、90，查找35比较元素是50、30、40。ASL（成功）=2.5，ASL（不成功）=3~4

46.用代码实现二分法查找的递归算法（以数组存储元素）
答：
int binarySearch(T value[], int n, T key)
{
return binarySearch(value, 0, n-1, key);
}
int binarySearch(T value[], int begin, int end, T key)
{
if (begin<=end)
{ int mid = (begin+end)/2;
if (value[mid]==key)
return mid;
if (key < value[mid])
return binarySearch(value, begin, mid-1, key);
return binarySearch(value, mid+1, end, key);
}
return -1;
}

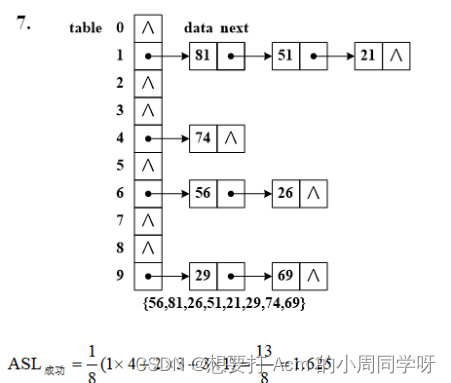
47. {56, 81, 26, 51, 21, 29, 74, 69}关键字序列，画出构造的散列表（链地址法），容量length=10，散列函数hash(key)=key % length；计算ASL（写出算式）。
    答：

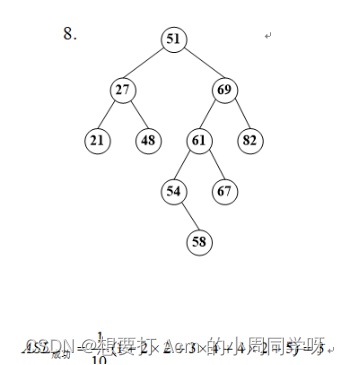
48.{51, 69, 82, 61, 27, 48, 51*, 54, 58, 67, 21}关键字序列，画出构造的二叉排序树，计算ASL（写出算式）。
答：

第九章
49.写出对关键字序列{65,92,87,25,38,56,46,12,25*}进行直接插入排序、希尔排序、快速排序、堆排序、归并排序（升序）的过程，并说明每种排序的稳定性。
答：
快速排序算法不稳定。
关键字序列：65 92 87 25 38 56 46 12 25*
0…8, vot=65, {25* 12 46 25 38 56} 65 {87 92}
0…5, vot=25, {12} 25* {46 25 38 56} 65 {87 92}
2…5, vot=46, 12 25* {38 25} 46 {56} 65 {87 92}
2…3, vot=38, 12 25* {25} 38 46 56 65 {87 92}
7…8, vot=87, 12 25* 25 38 46 56 65 87 {92}