GAMES101：作业6记录

news2024/11/17 5:47:58

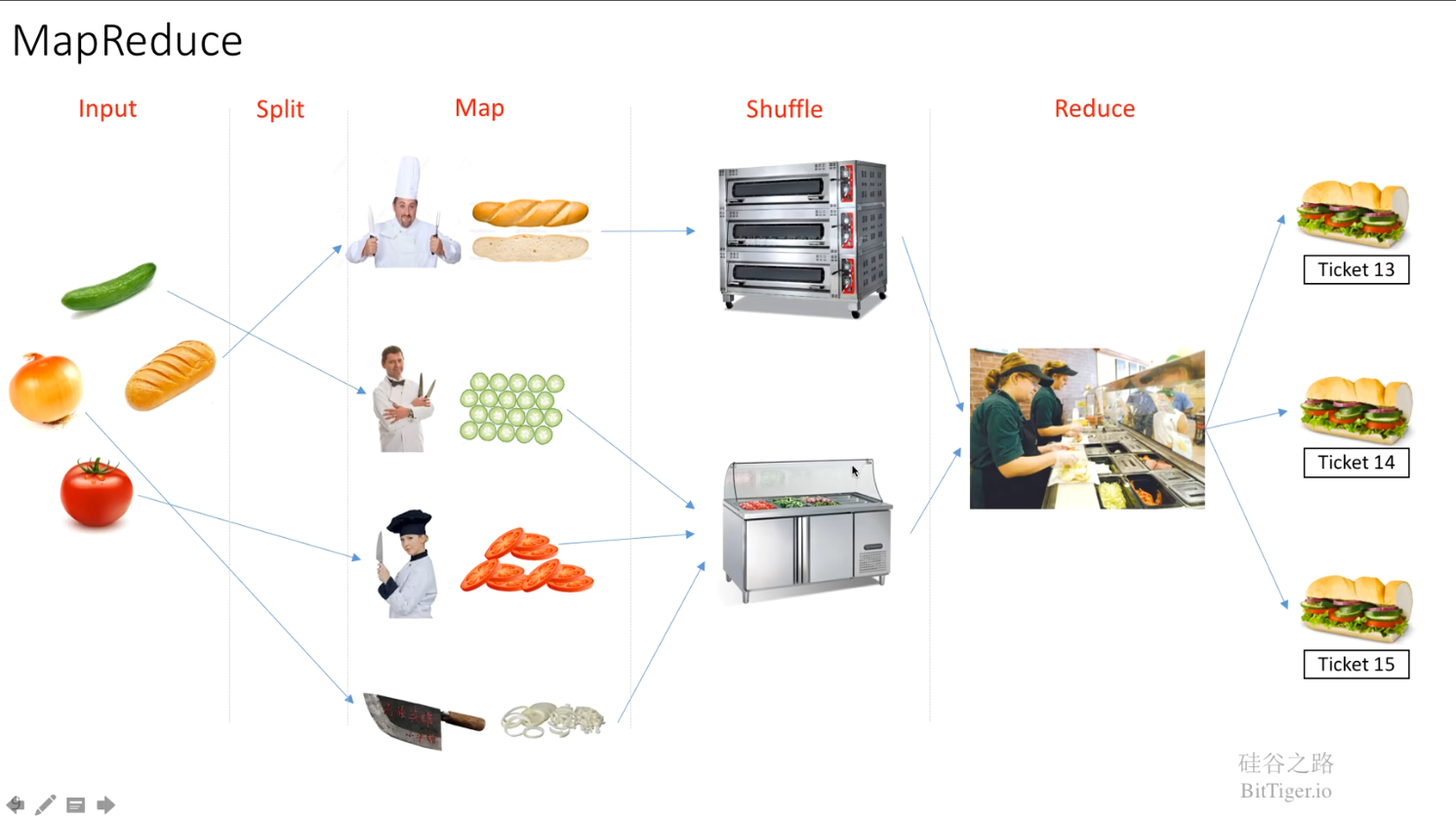
1 总览

在之前的编程练习中,我们实现了基础的光线追踪算法,具体而言是光线传输、光线与三角形求交。我们采用了这样的方法寻找光线与场景的交点:遍历场景中的所有物体,判断光线是否与它相交。在场景中的物体数量不大时,该做法可以取得良好的结果,但当物体数量增多、模型变得更加复杂,该做法将会变得非常低效。因此,我们需要加速结构来加速求交过程。在本次练习中,我们重点关注物体划分算法 Bounding Volume Hierarchy (BVH)。本练习要求你实现 Ray-BoundingVolume 求交与 BVH 查找。

首先,你需要从上一次编程练习中引用以下函数:

  • Render() in Renderer.cpp: 将你的光线生成过程粘贴到此处,并且按照新框
    架更新相应调用的格式。
  • Triangle::getIntersection in Triangle.hpp: 将你的光线-三角形相交函数粘贴到此处,并且按照新框架更新相应相交信息的格式。

在本次编程练习中,你需要实现以下函数:

  • IntersectP(const Ray& ray, const Vector3f& invDir, const std::array<int, 3>& dirIsNeg) in Bounds3.hpp: 这个函数的作用是判断包围盒 BoundingBox 与光线是否相交,你需要按照课程介绍的算法实现求交过程。
  • getIntersection(BVHBuildNode* node, const Ray ray) in BVH.cpp: 建立 BVH 之后,我们可以用它加速求交过程。该过程递归进行,你将在其中调用你实现的 Bounds3::IntersectP.

2. 实现

Render()的实现

光线生成，这里的eye_pos被移动到了(-1,5,10)，表示的是相机的位置，和作业5不一样，揣测代码的意思eye_pos已经是世界坐标了，而scene默认的fov是90，所以，这说明相机平面中心坐标其实等价于移动到了(-1,5,9)的位置（回想作业5相机的位置是(0,0,0)，而相机平面中心的坐标是(0,0,-1)）。和作业5不同，这里的ray的起点应该是eye_pos。

void Renderer::Render(const Scene& scene)
{
    std::vector<Vector3f> framebuffer(scene.width * scene.height);

    float scale = tan(deg2rad(scene.fov * 0.5));
    float imageAspectRatio = scene.width / (float)scene.height;
    Vector3f eye_pos(-1, 5, 10);
    int m = 0;
    for (uint32_t j = 0; j < scene.height; ++j) {
        for (uint32_t i = 0; i < scene.width; ++i) {
            // generate primary ray direction
            float x = (2 * (i + 0.5) / (float)scene.width - 1) *
                      imageAspectRatio * scale;
            float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
            // TODO: Find the x and y positions of the current pixel to get the
            // direction
            //  vector that passes through it.
            // Also, don't forget to multiply both of them with the variable
            // *scale*, and x (horizontal) variable with the *imageAspectRatio*

             Vector3f dir = normalize(Vector3f(x, y, -1)); // Don't forget to normalize this direction!
            Ray ray(eye_pos, dir);
            framebuffer[m++] = scene.castRay(ray, 0); 
            // Don't forget to normalize this direction!

        }
        UpdateProgress(j / (float)scene.height);
    }
    UpdateProgress(1.f);

    // save framebuffer to file
    FILE* fp = fopen("binary.ppm", "wb");
    (void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
    for (auto i = 0; i < scene.height * scene.width; ++i) {
        static unsigned char color[3];
        color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
        color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
        color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
        fwrite(color, 1, 3, fp);
    }
    fclose(fp);    
}

Triangle::getIntersection()的实现

inline Intersection Triangle::getIntersection(Ray ray)
{
    Intersection inter;

    if (dotProduct(ray.direction, normal) > 0)
        return inter;
    double u, v, t_tmp = 0;
    Vector3f pvec = crossProduct(ray.direction, e2);
    double det = dotProduct(e1, pvec);
    if (fabs(det) < EPSILON)
        return inter;

    double det_inv = 1. / det;
    Vector3f tvec = ray.origin - v0;
    u = dotProduct(tvec, pvec) * det_inv;
    if (u < 0 || u > 1)
        return inter;
    Vector3f qvec = crossProduct(tvec, e1);
    v = dotProduct(ray.direction, qvec) * det_inv;
    if (v < 0 || u + v > 1)
        return inter;
    t_tmp = dotProduct(e2, qvec) * det_inv;
    if (t_tmp < 0)
        return inter;
    // TODO find ray triangle intersection
    inter.happened = true;
    inter.coords = ray.origin + t_tmp * ray.direction;
    inter.normal = this->normal;
    inter.distance = t_tmp;
    inter.obj = this;
    inter.m = this->m;

    return inter;
}

TODO前面已经写好了我们在作业5写的Möller-Trumbore算法，不过我这里多加了一步判断，防止光线是反向的也计算出交点：

if (t_tmp < 0)
    return inter;

既然我们已经得到了交点，现在就是给交点的属性赋值了，如上面的代码所示:

happened: 是否发生相交
coords: 交点的世界坐标
normal: 交点的法向量
distance: 交点和相机的距离
obj: 物体
m: 材料属性

Bounds3::IntersectP()的实现

基本的思路是按照下面这张图来得到t_enter和t_exit

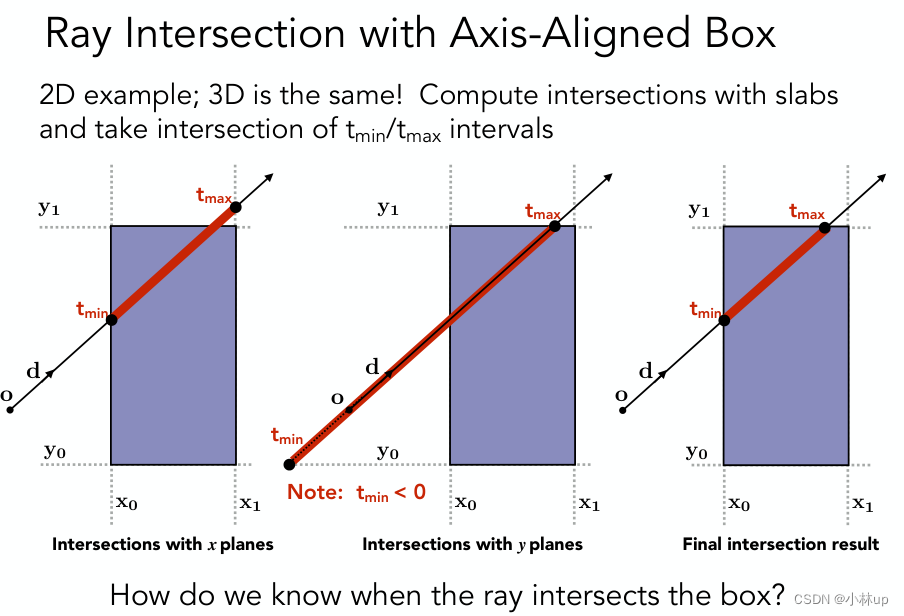
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
代码里使用了invDir因为乘法比除法更快，而dirIsNeg根据提示是说光线方向的三个分量是否大于零，例如对包围盒的x平面而言，包围盒有两个x平面 x = p M i n . x x=pMin.x x=pMin.x和 x = p M a x . x x=pMax.x x=pMax.x，如果光线的x方向分量大于0，说明先进入 x = p M i n . x x=pMin.x x=pMin.x这个平面，而从 x = p M a x . x x=pMax.x x=pMax.x离开，反之如果光线的x方向分量小于0，说明先进入了 x = p M a x . x x=pMax.x x=pMax.x这个平面，而从 x = p M i n . x x=pMin.x x=pMin.x平面离开。所以这里用dirIsNeg判断，如果分量小于0，则交换tEnter和tExit对应的分量。

判断和包围盒有交点的条件是：

t E n t e r < t E x i t t_{Enter} < t_{Exit} tEnter​<tExit​且 t E x i t ≥ 0 t_{Exit} \ge 0 tExit​≥0

inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
                                const std::array<int, 3>& dirIsNeg) const
{
    // invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
    // dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
    // TODO test if ray bound intersects
    Vector3f vec_tEnter = (pMin - ray.origin) * invDir;
    Vector3f vec_tExit = (pMax - ray.origin) * invDir;
    
    
    if (!dirIsNeg[0])
        std::swap(vec_tEnter.x, vec_tExit.x);
    if (!dirIsNeg[1])
        std::swap(vec_tEnter.y, vec_tExit.y);
    if (!dirIsNeg[2])
        std::swap(vec_tEnter.z, vec_tExit.z);

    float tEnter = std::max(vec_tEnter.x, std::max(vec_tEnter.y, vec_tEnter.z));
    float tExit = std::min(vec_tExit.x, std::min(vec_tExit.y, vec_tExit.z));

    if (tEnter <  tExit && tExit >= 0)
        return true;
    else
        return false;
    
}

BVH.cpp-getIntersection()的实现

基本的实现思路如下图算法所示：

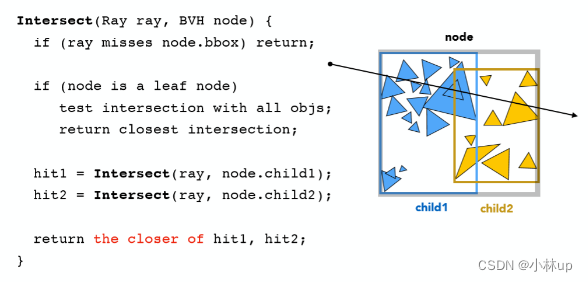
在这里插入图片描述

递归二叉树节点，如果发现节点的包围盒没有被光线打中，则返回一个默认的Intersection，如果发现节点遍历到了叶子节点，则返回这个节点的物体的交点的信息，否则用hitLeft记录左子树的交点，用hitRight记录右子树的交点，比较两个子树的交点和光线的距离，返回更小的那一个。

Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
    // TODO Traverse the BVH to find intersection
    if (!node->bounds.IntersectP(ray, ray.direction_inv, std::array<int, 3>({ray.direction.x > 0, ray.direction.y > 0, ray.direction.z > 0})))
        return Intersection();

    if (node->left == nullptr && node->right == nullptr)
        return node->object->getIntersection(ray);

    Intersection hitLeft = BVHAccel::getIntersection(node->left, ray);
    Intersection hitRight = BVHAccel::getIntersection(node->right, ray);

    return hitLeft.distance < hitRight.distance ? hitLeft : hitRight;
}

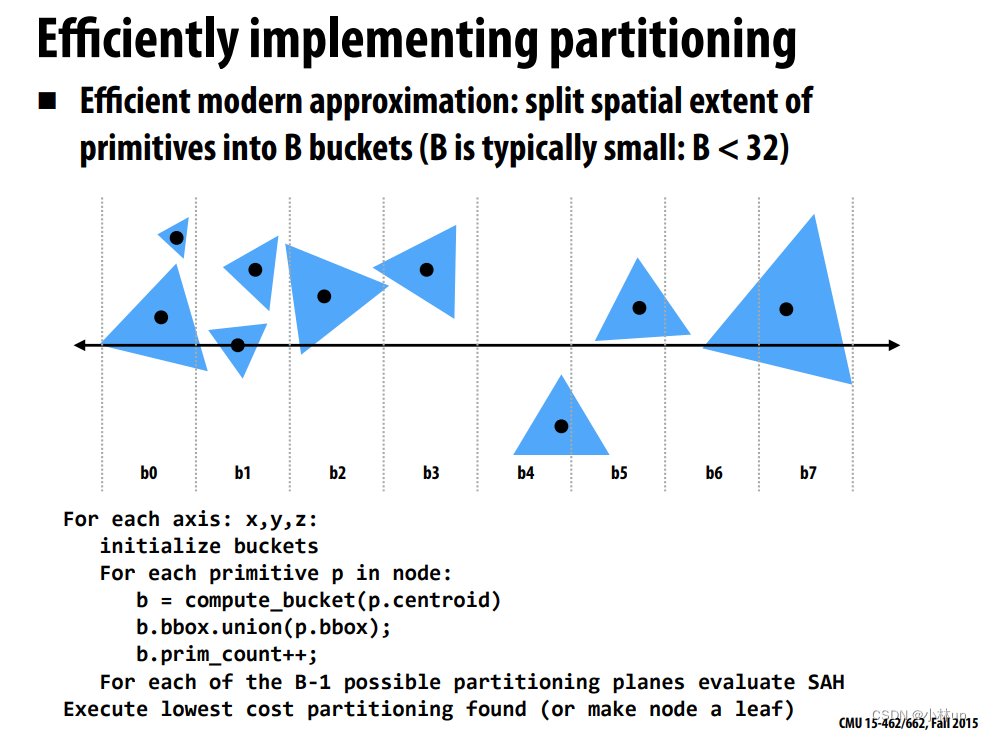
在这里插入图片描述
在这里插入图片描述

提高部分：SAH的实现

知乎的这篇文章讲得很好：PBRT-E4.3-层次包围体(BVH)（一）

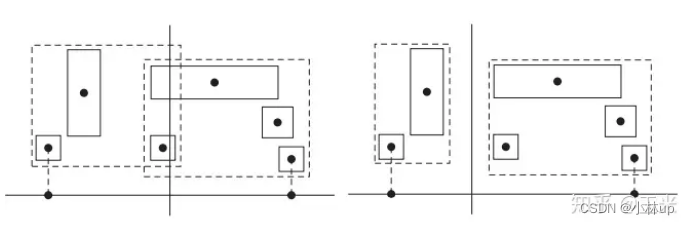
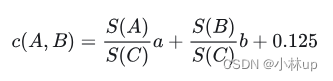
在这里插入图片描述
在这里插入图片描述

我们计算不同划分下的代价，我们希望代价可以最小，这样包围盒求交也最小，递归计算的消耗也会变小。

一种方法是划分各个桶的方法，在总的节点的包围盒计算每个片体质心所在的桶的序号，然后桶也增加在这个桶里的片体的个数和所有片体的包围盒，这样计算时间也是4s，没什么太大的差别，这里的代码先使用了排序，然后通过寻找最低的cost找到划分的指针和begin指针的差值，用迭代器给leftshapes和rightshapes赋值

在这里插入图片描述

BVHBuildNode* BVHAccel::recursiveBuild_SAH(std::vector<Object*> objects)
{
    BVHBuildNode* node = new BVHBuildNode();

    // Compute bounds of all primitives in BVH node
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    if (objects.size() == 1) {
    // Create leaf _BVHBuildNode_
    node->bounds = objects[0]->getBounds();
    node->object = objects[0];
    node->left = nullptr;
    node->right = nullptr;
    return node;
    }
    else if (objects.size() == 2) {
        node->left = recursiveBuild_SAH(std::vector{objects[0]});
        node->right = recursiveBuild_SAH(std::vector{objects[1]});

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        Bounds3 centroidBounds;
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
                Union(centroidBounds, objects[i]->getBounds().Centroid());
        int dim = centroidBounds.maxExtent();
        switch (dim) {
        case 0:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().x <
                    f2->getBounds().Centroid().x;
            });
            break;
        case 1:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().y <
                    f2->getBounds().Centroid().y;
            });
            break;
        case 2:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().z <
                    f2->getBounds().Centroid().z;
            });
            break;
        }

        float boundsArea = bounds.SurfaceArea();
        const int bucketNum = 10;
        Bucket bucket[bucketNum];
        for (int i = 0; i < objects.size(); ++i)
        {
            int b;
            switch (dim)
            {
            case 0: b = centroidBounds.Offset(objects[i]->getBounds().Centroid()).x * bucketNum;
                break;
            case 1: b = centroidBounds.Offset(objects[i]->getBounds().Centroid()).y * bucketNum;
                break;
            case 2: b = centroidBounds.Offset(objects[i]->getBounds().Centroid()).z * bucketNum;
                break;
            }
            if (b == bucketNum)
                b = bucketNum - 1;
            bucket[b].bounds = Union(bucket[b].bounds, objects[i]->getBounds());
            bucket[b].cnt++;
        }

        float costRes = std::numeric_limits<double>::infinity();
        int partitionInd = 0;
        int offset = 0;
        for (int i = 0; i < bucketNum - 1; ++i)
        {
            Bounds3 boundsLeft, boundsRight;
            int cntLeft = 0, cntRight = 0;
            for (int j = 0; j < i + 1; ++j)
            {
                cntLeft += bucket[j].cnt;
                boundsLeft = Union(boundsLeft, bucket[j].bounds);
            }
            for (int j = i + 1; j < bucketNum; ++j)
            {
                cntRight += bucket[j].cnt;
                boundsRight = Union(boundsRight, bucket[j].bounds);
            }
            float cost = cntLeft * boundsLeft.SurfaceArea() / boundsArea + cntRight * boundsRight.SurfaceArea() / boundsArea + 0.125f;
            if (cost < costRes)
            {
                partitionInd = i;
                costRes = cost;
                offset = cntLeft;
            }
        }

        auto beginning = objects.begin();
        auto midding = objects.begin() + offset;
        auto ending = objects.end();
        auto leftshapes = std::vector<Object*>(beginning, midding);
        auto rightshapes = std::vector<Object*>(midding, ending);

        node->left = recursiveBuild_SAH(leftshapes);
        node->right = recursiveBuild_SAH(rightshapes);

        node->bounds = Union(node->left->bounds, node->right->bounds);
    }
    
    return node;
}

我们需要定义结构体Bucket来放置桶，这里在BVH.hpp里进行了定义。

BVH.hpp

struct Bucket
{
    int cnt = 0;
    Bounds3 bounds;
};

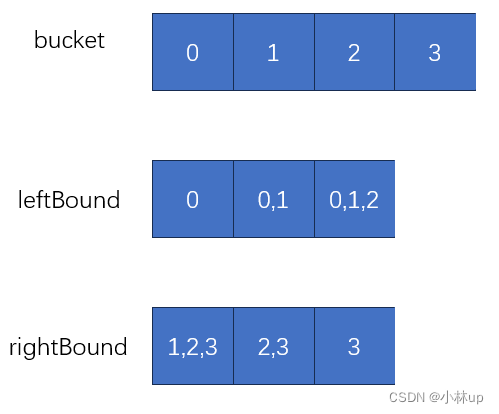
上面的写法每次计算leftBound和rightBount都要重新计算一遍，进行了很多重复计算，如果能保存中间结果呢可以减少重复计算，说不定提高计算效率，这里和力扣的238.除自身以外数组的乘积的思路很像

这里举个例子，比如bucket每个区间里各放有0,1,2,3四个片元，leftBound就放bucket左区间的片元的包围盒，rightBound放bucket右区间的片元的包围盒：

在这里插入图片描述
以bucket[1]为界（bucket[1]包含在左包围盒里），0,1包含在左包围盒，对应的是leftBound[1]，2,3包含在右包围盒，对应的是rightBound[1]

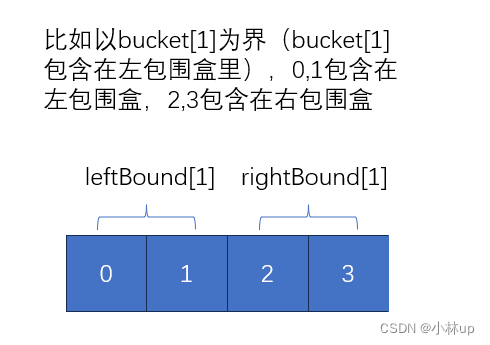
在这里插入图片描述

相邻的包围盒我们可以推得有递推公式，思路是包含前一个小区间的大包围盒和当前小区间的包围盒合并就可以得到包含当前小区间的大包围盒：

l e f t B o u n d [ i ] = U n i o n ( b u c k e t [ i ] . g e t B o u n d ( ) , l e f t B o u n d [ i − 1 ] ) leftBound[i] = Union(bucket[i].getBound(), leftBound[i-1]) leftBound[i]=Union(bucket[i].getBound(),leftBound[i−1])
r i g h t B o u n d [ i ] = U n i o n ( b u c k e t [ i + 1 ] . g e t B o u n d ( ) , r i g h t B o u n d [ i + 1 ] ) rightBound[i] = Union(bucket[i+1].getBound(), rightBound[i+1]) rightBound[i]=Union(bucket[i+1].getBound(),rightBound[i+1])

另外排序是不是也消耗了一点时间，下面的代码把排序给去掉了：

BVHBuildNode* BVHAccel::recursiveBuild_SAH(std::vector<Object*> objects)
{
    BVHBuildNode* node = new BVHBuildNode();

    // Compute bounds of all primitives in BVH node
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    if (objects.size() == 1) {
    // Create leaf _BVHBuildNode_
    node->bounds = objects[0]->getBounds();
    node->object = objects[0];
    node->left = nullptr;
    node->right = nullptr;
    return node;
    }
    else if (objects.size() == 2) {
        node->left = recursiveBuild_SAH(std::vector{objects[0]});
        node->right = recursiveBuild_SAH(std::vector{objects[1]});

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        Bounds3 centroidBounds;
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
                Union(centroidBounds, objects[i]->getBounds().Centroid());
        int dim = centroidBounds.maxExtent();

        float boundsArea = bounds.SurfaceArea();
        const int bucketNum = 10;
        Bucket bucket[bucketNum];
        for (auto& object: objects)
        {
            int b;
            switch (dim)
            {
            case 0: b = centroidBounds.Offset(object->getBounds().Centroid()).x * bucketNum;
                break;
            case 1: b = centroidBounds.Offset(object->getBounds().Centroid()).y  * bucketNum;
                break;
            case 2: b = centroidBounds.Offset(object->getBounds().Centroid()).z  * bucketNum;
                break;
            }
            if (b == bucketNum)
                b = bucketNum - 1;
            bucket[b].bounds = Union(bucket[b].bounds, object->getBounds());
            bucket[b].cnt++;
        }



        std::vector<Bounds3> leftBound(bucketNum - 1);
        std::vector<Bounds3> rightBound(bucketNum - 1);
        leftBound[0] = bucket[0].bounds;
        rightBound[bucketNum - 2] = bucket[bucketNum - 1].bounds;
        for (int i = 1; i < bucketNum - 1; ++i)
        {
            leftBound[i] = Union(leftBound[i - 1], bucket[i].bounds);
        }
           
        for (int i = bucketNum - 3; i >= 0; --i)
        {
            rightBound[i] = Union(rightBound[i + 1], bucket[i + 1].bounds);
        }
            

        int cntLeft = 0;
        int cntRight = objects.size();
        float costRes = std::numeric_limits<double>::infinity();
        int partitionInd = 0;
        for (int i = 0; i < bucketNum - 1; ++i)
        {
            cntLeft = cntLeft + bucket[i].cnt;
            cntRight = cntRight - bucket[i].cnt;
            if (cntLeft && cntRight)
            {
                float cost = cntLeft * leftBound[i].SurfaceArea() / boundsArea + cntRight * rightBound[i].SurfaceArea() / boundsArea + 0.125f;
                if (cost < costRes)
                {
                    partitionInd = i;
                    costRes = cost;
                }
            }
            
        }
        auto leftshapes = std::vector<Object*>();
        auto rightshapes = std::vector<Object*>();
        for (auto& object: objects)
        {
            int b;
            switch (dim)
            {
            case 0: b = centroidBounds.Offset(object->getBounds().Centroid()).x * bucketNum;
                break;
            case 1: b = centroidBounds.Offset(object->getBounds().Centroid()).y * bucketNum;
                break;
            case 2: b = centroidBounds.Offset(object->getBounds().Centroid()).z * bucketNum;
                break;
            }
            if (b == bucketNum)
                b = bucketNum - 1;
            if (b <= partitionInd)
                leftshapes.push_back(object);
            else
                rightshapes.push_back(object);
        }

        node->left = recursiveBuild_SAH(leftshapes);
        node->right = recursiveBuild_SAH(rightshapes);

        node->bounds = Union(node->left->bounds, node->right->bounds);
    }
    
    return node;
}

结果还是一样花了4秒渲染完。

另一种写法是将所有图元按照数量均匀划分成了B个部分，然后计算代价，这样划分比较快，但是好像没有用到桶的划分。

BVHBuildNode* BVHAccel::recursiveBuild_SAH(std::vector<Object*> objects)
{
        BVHBuildNode* node = new BVHBuildNode();

    // Compute bounds of all primitives in BVH node
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    if (objects.size() == 1) {
    // Create leaf _SAHBuildNode_
    node->bounds = objects[0]->getBounds();
    node->object = objects[0];
    node->left = nullptr;
    node->right = nullptr;
    return node;
    }
    else if (objects.size() == 2) {
        node->left = recursiveBuild_SAH(std::vector{objects[0]});
        node->right = recursiveBuild_SAH(std::vector{objects[1]});

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        Bounds3 centroidBounds;
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
                Union(centroidBounds, objects[i]->getBounds().Centroid());
        int dim = centroidBounds.maxExtent();
        switch (dim) {
        case 0:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().x <
                    f2->getBounds().Centroid().x;
            });
            break;
        case 1:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().y <
                    f2->getBounds().Centroid().y;
            });
            break;
        case 2:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().z <
                    f2->getBounds().Centroid().z;
            });
            break;
        }
        auto beginning = objects.begin();
        auto ending = objects.end();
        
        float midIdx = 1;
        int bucketNum = 10;
        float costRes = std::numeric_limits<double>::infinity();
        float nodeArea = bounds.SurfaceArea();
        for (int i = 1; i < bucketNum; ++i)
        {
            auto mid_temp = objects.begin() + std::max(1, (int)(objects.size() * (float)i / bucketNum));
            auto leftshapes = std::vector<Object*>(beginning, mid_temp);
            auto rightshapes = std::vector<Object*>(mid_temp, ending);
            assert(objects.size() == (leftshapes.size() + rightshapes.size()));
            Bounds3 leftBounds, rightBounds;
            for (int j = 0; j < leftshapes.size(); ++j)
                leftBounds = Union(leftBounds, leftshapes[j]->getBounds());
            for (int j = 0; j < rightshapes.size(); ++j)
                rightBounds = Union(rightBounds, rightshapes[j]->getBounds());
            float leftArea = leftBounds.SurfaceArea();
            float rightArea = rightBounds.SurfaceArea();
            float cost = leftArea / nodeArea * leftshapes.size() + rightArea / nodeArea * rightshapes.size() + 0.125f;
            if (cost < costRes)
            {
                midIdx = i;
                costRes = cost;
            }
        }

        auto middling = objects.begin() + std::max(1, (int)(objects.size() * (float)midIdx / bucketNum));
        auto leftshapes = std::vector<Object*>(beginning, middling);
        auto rightshapes = std::vector<Object*>(middling, ending);

        assert(objects.size() == (leftshapes.size() + rightshapes.size()));

        node->left = recursiveBuild_SAH(leftshapes);
        node->right = recursiveBuild_SAH(rightshapes);

        node->bounds = Union(node->left->bounds, node->right->bounds);
    }
    return node;
}

在这里插入图片描述
时间上也是4s。

3. 其他代码批注

BVHAccel::recursiveBuild()

这个函数的作用是递归的建立BVH的数，最后返回根节点，首先先把所有物体的包围盒得到，然后如果物体的个数为1，创建叶子节点，如果物体的个数是2，两个物体分别作为左右子树，如果物体的个数大于2，那么找当前节点内每个物体的包围盒质心的总和（Union），并且用maxExtent函数找这个包围盒最长的轴，沿最长的轴对物体进行排序，然后按排序的结果划分左子树和右子树。

BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects)
{
    BVHBuildNode* node = new BVHBuildNode();

    // Compute bounds of all primitives in BVH node
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    if (objects.size() == 1) {
        // Create leaf _BVHBuildNode_
        node->bounds = objects[0]->getBounds();
        node->object = objects[0];
        node->left = nullptr;
        node->right = nullptr;
        return node;
    }
    else if (objects.size() == 2) {
        node->left = recursiveBuild(std::vector{objects[0]});
        node->right = recursiveBuild(std::vector{objects[1]});

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        Bounds3 centroidBounds;
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
                Union(centroidBounds, objects[i]->getBounds().Centroid());
        int dim = centroidBounds.maxExtent();
        switch (dim) {
        case 0:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().x <
                       f2->getBounds().Centroid().x;
            });
            break;
        case 1:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().y <
                       f2->getBounds().Centroid().y;
            });
            break;
        case 2:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().z <
                       f2->getBounds().Centroid().z;
            });
            break;
        }

        auto beginning = objects.begin();
        auto middling = objects.begin() + (objects.size() / 2);
        auto ending = objects.end();

        auto leftshapes = std::vector<Object*>(beginning, middling);
        auto rightshapes = std::vector<Object*>(middling, ending);

        assert(objects.size() == (leftshapes.size() + rightshapes.size()));

        node->left = recursiveBuild(leftshapes);
        node->right = recursiveBuild(rightshapes);

        node->bounds = Union(node->left->bounds, node->right->bounds);
    }

    return node;
}

maxExtent的实现，用来获取最长的轴，0,1,2,分别对应x轴，y轴和z轴：

int Bounds::maxExtent() const
    {
        Vector3f d = Diagonal();
        if (d.x > d.y && d.x > d.z)
            return 0;
        else if (d.y > d.z)
            return 1;
        else
            return 2;
    }

Bounds3

这个建立的是一个三维的包围盒，对于一个长方体我们只需要两个角点就可以把包围盒的信息记录下来，两个角点分别是最靠近原点和最远离原点的，看下代码中的pMin和pMax的定义就知道了

  • Vector3f Diagonal()：获得包围盒长宽高的矢量
  • double SurfaceArea() : 获得包围盒的表面积
  • Vector3f Centroid()：获得包围盒的中心
  • Bounds3 Intersect(const Bounds3& b)：和另一个包围盒相交后的新的包围盒
  • Vector3f Offset(const Vector3f& p)：p在包围盒各维度长度的占比
  • bool Overlaps(const Bounds3& b1, const Bounds3& b2)：两个包围盒是不是有重叠
  • bool Inside(const Vector3f& p, const Bounds3& b)：点p是不是在包围盒b内
  • Bounds3 Union(const Bounds3& b1, const Bounds3& b2)：两个包围盒合并为一个更大的包围盒
  • Bounds3 Union(const Bounds3& b, const Vector3f& p)：添加点p以后的新的包围盒

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1363521.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

前端JS加密对抗由浅入深-1

前端JS加密对抗由浅入深-1

前言&#xff1a; 本文主要讲解&#xff0c;针对前端加密数据传输站点&#xff0c;如何进行动态调试以获取加密算法、秘钥&#xff0c;本次实验不涉及漏洞挖掘&#xff0c;仅为学习演示&#xff0c;环境为本地搭建环境 此次站点加密方式为AES加密方式&#xff0c;现如今越来越…
阅读更多...
【STM32】STM32学习笔记-DMA直接存储器存储(23)

【STM32】STM32学习笔记-DMA直接存储器存储(23)

00. 目录 文章目录 00. 目录01. DMA简介02. DMA主要特性03. 存储器映像04. DMA框图05. DMA基本结构06. DMA请求07. 数据宽度与对齐08. 数据转运DMA09. ADC扫描模式DMA10. 附录 01. DMA简介 小容量产品是指闪存存储器容量在16K至32K字节之间的STM32F101xx、STM32F102xx和STM32F…
阅读更多...
Mybatis-Mapper代理开发

Mybatis-Mapper代理开发

Mapper代理开发 目的使用Mapper代理方式入门1.定义与SQL映射文件同名的Mapper接口&#xff0c;并且将Mapper接口和SQL映射文件放置在同一目录下首先新建一个Mapper接口编译mybatis-demo更改sql映射文件路径 2.设置SQL映射文件的namespace属性为Mapper接口全限定名3.在Mapper 接…
阅读更多...
论文浅尝 | 以词-词关系进行分类的统一命名实体识别

论文浅尝 | 以词-词关系进行分类的统一命名实体识别

笔记整理&#xff1a;曹旭东&#xff0c;东南大学硕士&#xff0c;研究方向为知识图谱构建、自然语言处理 链接&#xff1a;https://arxiv.org/abs/2112.10070 1. 动机 在以前的工作中&#xff0c;命名实体识别&#xff08;NER&#xff09;涉及的主要问题有三种类型&#xff0c…
阅读更多...
Java数据结构：1. 数据结构前置知识

Java数据结构：1. 数据结构前置知识

文章目录 一、初识数据结构二、初识集合框架1. 什么是集合框架2. 集合框架的重要性3. 背后所涉及的数据结构以及算法 三、时间复杂度空间复杂度1. 算法效率2. 时间复杂度&#xff08;1&#xff09;概念&#xff08;2&#xff09;大O的渐进表示法&#xff08;3&#xff09;推导大…
阅读更多...
欧几里得算法总结

欧几里得算法总结

知识概览 欧几里得算法也叫辗转相除法&#xff0c;核心原理是(a, b) (b, a mod b)&#xff0c;时间复杂度为O(logn)。 例题展示 题目链接 活动 - AcWing 系统讲解常用算法与数据结构&#xff0c;给出相应代码模板&#xff0c;并会布置、讲解相应的基础算法题目。https://www…
阅读更多...
了解统计分类中的贝叶斯理论误差限

了解统计分类中的贝叶斯理论误差限

一、介绍 统计分类和机器学习领域正在不断发展&#xff0c;努力提高预测模型的准确性和效率。这些进步的核心在于一个基本基准&#xff0c;即贝叶斯理论误差极限。这个概念深深植根于概率和统计学&#xff0c;是理解分类算法的局限性和潜力的基石。本文深入探讨了贝叶斯错误率的…
阅读更多...
Java技术栈 —— Hadoop入门（一）

Java技术栈 —— Hadoop入门（一）

Java技术栈 —— Hadoop入门&#xff08;一&#xff09; 一、Hadoop第一印象二、安装Hadoop三、Hadoop解析3.1 Hadoop生态介绍3.1.1 MapReduce - 核心组件3.1.2 HDFS - 核心组件3.1.3 YARN - 核心组件3.1.4 其它组件3.1.4.1 HBase3.1.4.2 Hive3.1.4.3 Spark 一、Hadoop第一印象…
阅读更多...
用通俗易懂的方式讲解：万字长文带你入门大模型

用通俗易懂的方式讲解：万字长文带你入门大模型

告别2023&#xff0c;迎接2024。大模型技术已成为业界关注焦点&#xff0c;你是否也渴望掌握这一领域却又不知从何学起&#xff1f; 本篇文章将特别针对入门新手&#xff0c;以浅显易懂的方式梳理大模型的发展历程、核心网络结构以及数据微调等关键技术。 如果你在阅读中收获…
阅读更多...
NJIT数据结构期末复习

NJIT数据结构期末复习

任何时候学习都不算晚&#xff0c;保持终身学习&#xff01;&#xff01;&#xff01; 数据结构期末复习 第一章 1.以下程序段的时间复杂是多少&#xff1f; int sum 0; for(i1;i<n;i) { for(j1;j<n;j) { sum; } } 答&#xff1a;O(n^2) 第二章 2.遍历单链表&…
阅读更多...
【计算机组成原理】总复习笔记（上）

【计算机组成原理】总复习笔记（上）

特别声明&#xff1a; 本文仅供参考&#xff0c;本文部分内容来自AI总结、网络搜集与个人实践。如果任何信息存在错误,欢迎读者批评指正。本文仅用于学习交流,不用作任何商业用途。 文章目录 第 1 章 计算机系统概述1.1 冯诺依曼计算机结构1.2 高级语言与机器级目标代码1.3 计算…
阅读更多...
【AI】搭建Windows Linux子系统（WSL2）CUDA环境

【AI】搭建Windows Linux子系统（WSL2）CUDA环境

0.准备工作 Windows本机安装CUDA Driver 首先去下载页面下载驱动文件 点击Get CUDA Driver进入下载页面&#xff0c;我看下载页面跟普通驱动下载页面相同&#xff0c;感觉应该不是单独的驱动&#xff0c;只要之前显卡已经安装好了CUDA的驱动&#xff0c;就可以先省略这一步。…
阅读更多...
使用 CMake 和 Ninja 构建 C/C++ 项目的教程

使用 CMake 和 Ninja 构建 C/C++ 项目的教程

使用 CMake 和 Ninja 构建 C/C 项目的教程 CMake 是一个跨平台的开源构建工具&#xff0c;它简化了项目的构建过程。而 Ninja 是一个快速、轻量级的构建系统&#xff0c;与 CMake 配合使用可以提高项目的构建效率。本教程将向你介绍如何使用 CMake 和 Ninja 来构建你的 C/C 项…
阅读更多...
灰色关联分析

灰色关联分析

&#xff08;相关性分析&#xff09;反映关系有多么紧密 “在系统发展过程中&#xff0c;若两个因素变化的趋势具有一致性&#xff0c;即同步变化程度较高&#xff0c;即可谓二者关联程度较高&#xff1b;反之&#xff0c;则较低。因此&#xff0c;灰色关联分析方法&#xff0…
阅读更多...
一文了解 DeFi 原生公链 Sei，以及钱包添加教程什么是Sei？

一文了解 DeFi 原生公链 Sei，以及钱包添加教程什么是Sei？

Sei&#xff0c;领先Layer 1公链&#xff0c;专攻加密资产交易。不局限于DeFi&#xff0c;还进军游戏、社交媒体和NFTs等领域&#xff0c;构建了多功能区块链生态系统。在众多公链中&#xff0c;Sei凭借卓越处理速度和技术创新崭露头角。独特共识机制和技术创新功不可没。作为通…
阅读更多...
【LeetCode每日一题】2807. 在链表中插入最大公约数（模拟+求最大公约数的6中写法）

【LeetCode每日一题】2807. 在链表中插入最大公约数（模拟+求最大公约数的6中写法）

2024-1-6 文章目录 [2807. 在链表中插入最大公约数](https://leetcode.cn/problems/insert-greatest-common-divisors-in-linked-list/)思路&#xff1a;模拟求最大公约数的几种方法&#xff1a; 1.暴力枚举法2.辗转相除法3.辗转相除法 ---递归调用4.辗转相除法 ---递归调用---…
阅读更多...
摄像头视频录制程序使用教程(Win10)

摄像头视频录制程序使用教程(Win10)

摄像头视频录制程序-Win10 &#x1f957;介绍&#x1f35b;使用说明&#x1f6a9;config.json 说明&#x1f6a9;启动&#x1f6a9;关闭&#x1f6a9;什么时候开始录制&#xff1f;&#x1f6a9;什么时候触发录制&#xff1f;&#x1f6a9;调参 &#x1f957;介绍 检测画面变化…
阅读更多...
每日一练：LeeCode-388. 文件的最长绝对路径【字符串、栈方法】

每日一练：LeeCode-388. 文件的最长绝对路径【字符串、栈方法】

本文是力扣LeeCode-388. 文件的最长绝对路径 学习与理解过程&#xff0c;本文仅做学习之用&#xff0c;对本题感兴趣的小伙伴可以出门左拐LeeCode。 假设有一个同时存储文件和目录的文件系统。下图展示了文件系统的一个示例&#xff1a; 这里将 dir 作为根目录中的唯一目录。…
阅读更多...
vue3+vite +element plus日历date picker中文显示

vue3+vite +element plus日历date picker中文显示

项目情况 element-plus 默认是英文模式&#xff0c;需要中文模式的话需要设置一下&#xff1a; 项目框架&#xff08;vue3&#xff09;&#xff1a;vite JS element-plus 版本&#xff1a;&#xff08;注意版本兼容&#xff0c;element plus 较低版本&#xff1a;1.xx.xx&a…
阅读更多...
【深度deepin】深度安装，jdk，tomcat，Nginx安装

【深度deepin】深度安装，jdk，tomcat，Nginx安装

目录 一 深度 1.1 介绍 1.2 与别的操作系统的优点 二 下载镜像文件及VM安装deepin 三 jdk&#xff0c;tomcat&#xff0c;Nginx安装 3.1 JDK安装 3.2 安装tomcat 3.3 安装nginx 一 深度 1.1 介绍 由深度科技社区开发的开源操作系统&#xff0c;基于Linux内核&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023