一、介绍
统计分类和机器学习领域正在不断发展,努力提高预测模型的准确性和效率。这些进步的核心在于一个基本基准,即贝叶斯理论误差极限。这个概念深深植根于概率和统计学,是理解分类算法的局限性和潜力的基石。本文深入探讨了贝叶斯错误率的本质、其对机器学习的影响以及其应用中面临的挑战。

即使在知识完美的世界中,不确定性的低语仍然存在。因为在概率和数据领域,贝叶斯误差极限证明了分类的固有缺陷,提醒我们追求理解是一个旅程,而不是目的地。
二、贝叶斯错误率的概念概述
贝叶斯错误率,通常称为贝叶斯风险或极限,是给定数据分布下任何分类器可实现的最小错误率。它代表了一个理想的阈值,其中错误完全是由于数据本身固有的重叠或噪声,而不是分类算法的不足。
贝叶斯误差极限的基础是贝叶斯定理,这是概率论的基本原理。它涉及条件概率,并提供了一个根据新证据更新概率估计的框架。
贝叶斯理论误差限,也称为贝叶斯错误率,是统计分类和机器学习中的基本概念。它代表任何分类器在预测新数据点的类别时可以实现的最低可能错误率。该限制由数据本身的固有噪声或重叠决定,并且是数据中不同类别本质上无法区分的程度的度量。
这是一个简单的解释:假设您有一个包含两类项目的数据集,例如苹果和橙子。完美的分类器总是能正确地将苹果识别为苹果,将橙子识别为橙子。然而,如果由于自然变化,某些苹果看起来与橙子一模一样(反之亦然),那么即使是最好的分类器也会在这些项目上犯错误。考虑到类之间固有的相似性(或重叠),贝叶斯错误率是任何分类器在此任务中可以实现的最低错误率。

贝叶斯错误率很重要,因为它可以作为分类器性能的理论基准。如果分类器的错误率接近贝叶斯率,则它的效果与给定数据的预期一样好。另一方面,如果分类器的错误率和贝叶斯率之间存在很大差距,则分类器的设计可能还有改进的空间。
在实践中,计算贝叶斯错误率可能具有挑战性,因为它需要完全了解数据集中类的真实基础分布。通常,真实分布是未知的,贝叶斯错误率只能估计。
三、机器学习中的贝叶斯错误率
3.1 错误率与性能
- 分类器性能基准测试:在机器学习的背景下,贝叶斯错误率是评估分类器性能的黄金标准。性能接近此限制的分类器被认为是最佳的,因为它可以有效地管理数据类别的不可区分的方面。
- 对模型选择和设计的影响:了解贝叶斯极限有助于选择合适的模型和设计算法。如果模型的性能显着偏离该理论极限,则表明模型本身或特征选择和预处理方面存在改进的潜力。
3.2 计算贝叶斯错误率的挑战
- 估计困难:应用贝叶斯错误率的主要挑战之一是其计算。精确的计算需要完整而精确地理解数据的潜在概率分布,这在现实场景中通常是不切实际或不可能的。
- 近似技术:已经开发了各种近似方法来估计贝叶斯错误率。其中包括交叉验证、引导和采用替代模型来近似底层数据分布等技术。
3.3 实际意义和局限性
- 实际应用:实际上,贝叶斯错误率提供了一个理论框架,用于理解医疗诊断、语音识别和金融预测等各个领域的分类局限性。
- 局限性和误解:虽然贝叶斯错误率是一个强大的概念,但认识到其局限性至关重要。它没有考虑其他重要方面,例如计算效率、可扩展性以及精度和召回率之间的权衡。
四、代码
为了使用 Python 演示贝叶斯理论误差限,我们将创建一个合成数据集,实现一个基本分类器,然后估计贝叶斯错误率。我们将使用 NumPy、Scikit-learn 和 Matplotlib 等库来完成此任务。该过程涉及以下步骤:
- 创建综合数据集:生成包含两个类的数据集,其中类有一些重叠,从而无法进行完美分类。
- 实现分类器:使用 Scikit-learn 中的标准分类器对数据进行分类。
- 估计贝叶斯错误率:由于我们可以控制数据集,因此我们可以通过了解基础分布来估计贝叶斯错误。
- 绘制结果:可视化数据集和分类决策边界。
让我们首先编写这些步骤的代码。
# @evertongomede
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
from matplotlib.colors import ListedColormap
# Step 1: Create a Synthetic Dataset
X, y = make_classification(n_samples=300, n_features=2, n_redundant=0, n_clusters_per_class=1, flip_y=0.1, class_sep=1.5, random_state=42)
# Step 2: Implement a Classifier
gnb = GaussianNB()
gnb.fit(X, y)
y_pred = gnb.predict(X)
# Calculate accuracy
accuracy = accuracy_score(y, y_pred)
# Step 3: Estimate the Bayes Error Rate
# For a synthetic dataset with known overlap, we can approximate the Bayes error rate.
# Here, we'll assume it's roughly equal to the flip_y parameter used to generate the dataset, which simulates the overlap.
bayes_error_rate = 0.1 # This is an approximation for this synthetic dataset
# Step 4: Plot the Results
cmap_light = ListedColormap(['#FFAAAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#0000FF'])
# Create mesh for background colors
h = .02 # step size in the mesh
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = gnb.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(figsize=(8, 6))
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title(f"2-Class classification with Gaussian Naive Bayes\nAccuracy: {accuracy:.2f}, Estimated Bayes Error Rate: {bayes_error_rate}")
plt.show()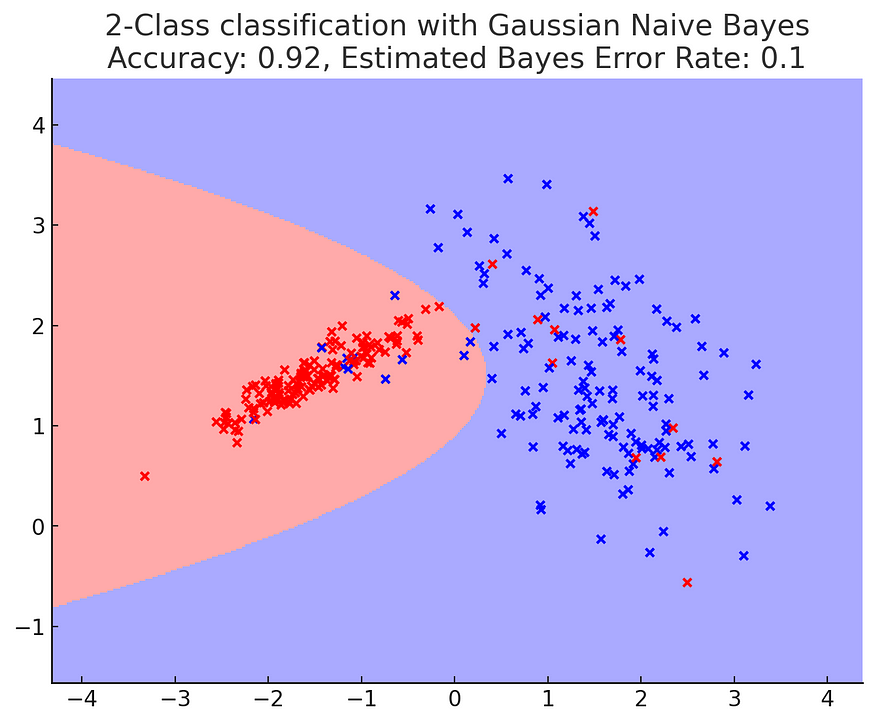
上图可视化了我们使用合成数据集和高斯朴素贝叶斯分类器进行实验的结果。背景中的不同颜色代表分类器的决策区域。这些点是数据样本,根据其真实类别着色。
- 准确性:我们的高斯朴素贝叶斯分类器的准确性显示在图的标题中。该值表示我们的分类器在此特定数据集上的执行情况。
- 估计贝叶斯错误率:对于此合成数据集,贝叶斯错误率近似于
flip_y数据集生成期间使用的参数。该参数在类之间引入了一些重叠(或噪声),模拟即使完美的分类器也会出错的场景。在我们的例子中,该值设置为 0.1,即 10%。
请记住,这是一个简化的说明。在现实场景中,估计贝叶斯错误率要复杂得多,因为它需要精确了解底层数据分布,而这通常是不可用的。
五、结论
贝叶斯理论误差限是理解统计分类和机器学习的关键概念。它为理论上可实现的分类准确性提供了基准,指导研究人员和从业者寻求更精致、更高效的模型。然而,这一限制的实际计算和应用仍然具有挑战性,凸显了机器学习的复杂性和动态性。随着技术和方法的进步,对接近甚至达到这一理论极限的模型的追求仍在继续,推动了机器学习领域的创新和卓越。