本篇博客主要详细讲解一下NB三人组排序，为什么叫NB三人组呢？因为他们的时间复杂度都为O(n log n)。第一篇博客讲解的是LowB三人组（冒泡排序，插入排序，选择排序），第三篇博客会讲解其他排序（基数排序，希尔排序和桶排序）

random和time库的用法在第一篇冒泡排序里讲解过。数据结构课设实验内容也在第一篇博客中。

概念：

堆排序是一种利用堆这种数据结构来进行排序的算法，它的时间复杂度为O(n log n)，具有很好的性能。它的主要特点是不稳定排序，且不适合小数据集。

归并排序是一种分治算法，它将待排序的序列分成若干个子序列，分别进行排序，然后将已排序的子序列合并成一个有序序列。它的时间复杂度也为O(n log n)，具有稳定性和适用于大数据集的特点。

快速排序是一种分治算法，它通过选取一个基准元素，将序列分成两部分，分别对两部分进行排序，然后递归地对子序列进行排序。它的时间复杂度为O(n log n)，具有不稳定性和适用于大数据集的特点。

堆排序：

首先讲解一下堆排序的过程，这里是构造大根堆，首先对数组进行建堆操作，建好堆以后对堆进行堆排序，之后再建堆，再排序 往复操作直到所有排序完成。

堆排序比较复杂，难度在于理解上。
这里就不详细讲解建堆过程，步骤过多。
如图：

代码及详细注释：

import random
import time
def sift(li, low, high):
    '''
    堆调整函数
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    '''
    i = low  # i最开始指向根节点
    j = 2*i + 1  # j开始时左孩子 因为这里的下标实际是数组的下标所以左孩子不是2*i,
    tmp = li[low]  # 把堆顶存起来
    while j <= high:  # 只要j位置有数
        if j + 1 <= high and li[j+1] > li[j]:  # 如果有右孩子并且右孩子比左孩子大
            j = j + 1  # j指向右孩子
        if li[j] > tmp:
            li[i] = li[j]
            i = j      # 往下看一层
            j = i*2 + 1
        else:          # tmp更大，把tmp放到i的位置上
            li[i] = tmp   # 把tmp放在某一级领导位置上
            break
    else:
        li[i] = tmp     # 把tmp放在叶子节点上

def heap_sort(li):
    n = len(li)
    for i in range((n-2)//2, -1, -1):
        # i表示建堆的时候调整的部分的根的小标
        sift(li, i, n-1)
    # 建堆完成了
    for i in range(n-1, -1, -1):
        # i 指向当前堆的最后一个元素
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i-1)  # i-1是新的high


li = [random.randint(1, 100000000) for i in range(10000)]
start = time.time()
print(li)
heap_sort(li)
print(li)
end = time.time()
print('运行时间：%s Seconds'%(end-start))

运行结果：

归并排序：

归并排序用的是分治法，把一个大问题化解为k个中问题，每个中问题再化解为k个小问题，直至问题化为最小可解的问题。对这些问题求解，再不断地合并结果，直至合并完毕。
如图：

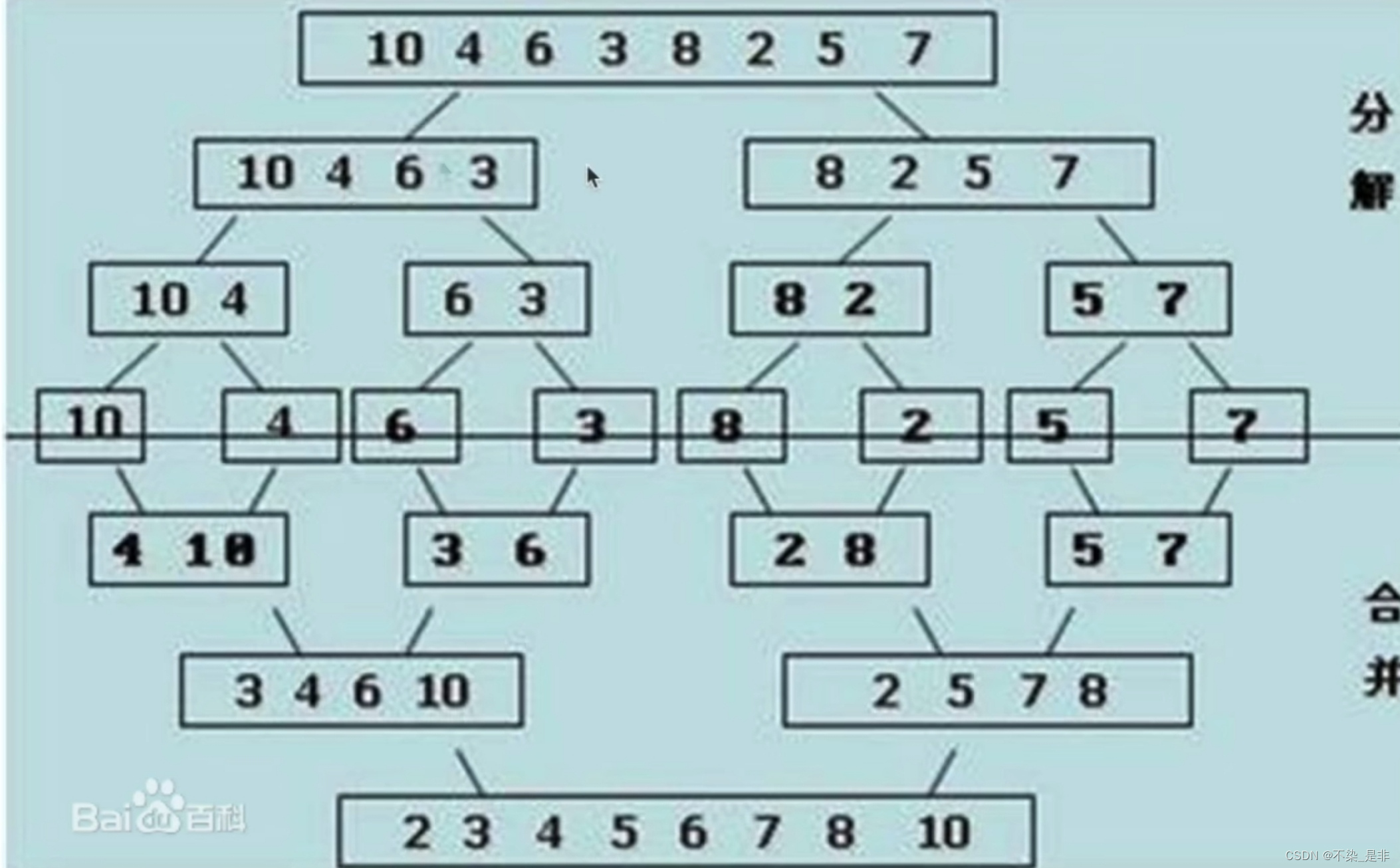
代码及详细注释：

import random
import time
def merge(li, low, mid, high):
    '''
    归并函数，用来合并两个有序序列
    :param li: 列表
    :param low: 左边有序序列的起始位置
    :param mid: 左边有序序列的结束位置
    :param high: 右边有序序列的结束位置
    :return:
    '''
    i = low
    j = mid + 1
    itmp = []
    while i <= mid and j <= high:  # 只要左右两边都有数
        if li[i] < li[j]:
            itmp.append(li[i])
            i += 1
        else:
            itmp.append(li[j])
            j += 1
    # while执行完，肯定有一部分没数了
    while i <= mid:
        itmp.append(li[i])
        i += 1
    while j <= high:
        itmp.append(li[j])
        j += 1
    li[low:high + 1] = itmp  # 将合并后的有序序列放回原列表

def merge_sort(li, low, high):
    '''
    归并排序函数
    :param li: 列表
    :param low: 起始位置
    :param high: 结束位置
    :return:
    '''
    if low < high:
        mid = (low + high) // 2  # 至少有两个元素，递归
        merge_sort(li, low, mid)  # 对左半部分进行归并排序
        merge_sort(li, mid + 1, high)  # 对右半部分进行归并排序
        merge(li, low, mid, high)  # 合并两个有序序列

li = [random.randint(1, 100000000) for i in range(10000)]
start = time.time()
print(li)
merge_sort(li, 0, len(li) - 1)
print(li)
end = time.time()
print('运行时间：%s Seconds'%(end-start))

归并排序比较好写但不好理解，这里跟大家讲一下具体理解，
def merge（）里代码的含义是一次归并的过程，比如 [2，4，5，7，1，3，6，8] 该数组从mid(索引3)开始左右两边有序，现在合并成一个有序数组，i 指向元素2，j指向元素1，两者比较，小的数（1）进新数组，然后指针j 后移一位，继续跟i指针指向的元素比较，小的进数组，一直重复，直到一边无数可比为止，然后把另一边的剩余未比较的数组全部入新数组。
def merge_sort（）函数作用是递归分解原数组，分解到只剩一个元素，最后再调用def merge()函数进行合并

运行结果：

快速排序：

快速排序是一种基于分治思想的排序算法，其过程可以描述如下：

1. 选择一个基准元素（通常是数组中的第一个元素）。
2. 将数组中小于基准元素的元素移动到基准元素的左边，大于基准元素的元素移动到右边，基准元素则位于最终排序位置。
3. 对基准元素左右两边的子数组分别进行快速排序，直到子数组长度为1或0。
   递归地重复步骤2和步骤3，直到整个数组有序。

如图：

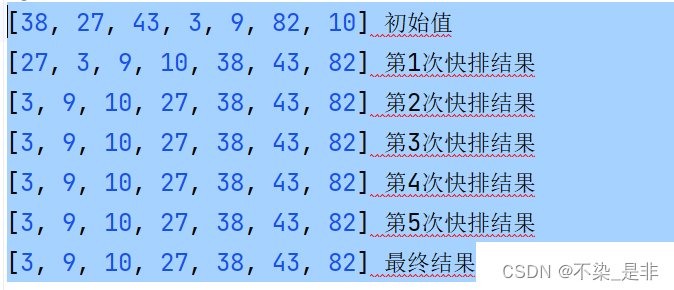
代码及详细注释：

import random
import time
def partition(li, left, right):
    '''
    划分函数，用于将列表分成两部分并返回中间位置
    :param li: 列表
    :param left: 左边界
    :param right: 右边界
    :return: 中间位置
    '''
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:  # 从右面找比tmp小的数
            right -= 1                            # 往左走一步
        else:
            li[left] = li[right]                  # 把右边的值写到左边空位上
        while left < right and li[left] <= tmp:   # 从左边找比tmp大的数
            left += 1
        else:
            li[right] = li[left]                  # 把左边的值写到右边空位上
    li[left] = tmp                                # 把tmp归位
    return left

def quick_sort(li, left, right):
    '''
    快速排序函数
    :param li: 列表
    :param left: 起始位置
    :param right: 结束位置
    :return:
    '''
    if left < right:  # 至少两个元素
        mid = partition(li, left, right)  # 划分并获取中间位置
        quick_sort(li, left, mid - 1)  # 对左半部分进行快速排序
        quick_sort(li, mid + 1, right)  # 对右半部分进行快速排序

li = [random.randint(1, 100000000) for i in range(10000)]
start = time.time()
print(li)
quick_sort(li, 0, len(li) - 1)
print(li)
end = time.time()
print('运行时间：%s Seconds'%(end-start))

快排要用双指针法，两个指针来遍历数组进行比较，直到指针相遇。递归调用的思想跟归并差不多

运行结果：

总结：

之前的LowB三人组是看代码里的注释就可以理解，没有必要讲。而NB三人组的每趟排序的详细过程步骤篇幅太长，不太好讲，也不好找图片，只能粗略带大家过一遍。

通过运行时间可以明显看出NB三人组的运行效率比LowB三人组快很多，不过NB三人组的算法思想稍微有点难理解，如果理解了代码还是较容易实现，我认为难点在递归调用的理解上面，每一趟的排序实现还是容易写出来的。排序综合还剩下最后一篇其他排序的讲解就结束了。