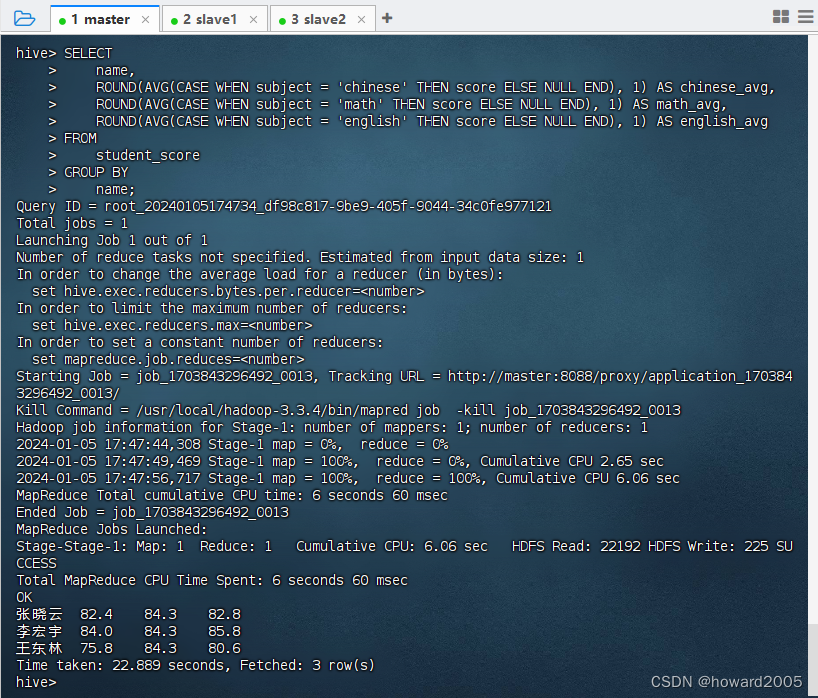
目录
一. 对偶格的格点
1.1 基本定义
1.2 对偶格的例子
1.3 对偶格的图形理解
二. 对偶格的格基
2.1 基本定义
2.2 对偶格的格基证明
三. 对偶格的行列式
3.1 满秩格
3.2 非满秩格
四. 重复对偶格
五. 对偶格的转移定理(transference theorem)
六. 对偶格的连续最小值
七. 对偶格的正交投影
八. 对偶格基的正交化
推荐先阅读:
格密码的基础概念-CSDN博客
一. 对偶格的格点
1.1 基本定义
对偶格(dual lattice)也被称之为倒易格(reciprocal lattice)。原来满秩的格写做,其对偶格的定义如下:
![]()
原来的格点和对偶格的任意(这两个字非常重要)格点相乘为整数即可。原来的格点如果为整数,那么对偶格里有可能会出现小数。此处代表n维实数空间,更准确来讲,对偶格应该在原来格的扩展空间内。那么对偶格更准确的定义,如下:
![]()
对偶格的右上角经常带“*”,代表格的扩展空间。
对偶格的重心在于,向量相乘为整数。当然,对偶格也是一种格,格的一些基本性质对偶格也具有。格和对偶格是成对出现的。
1.2 对偶格的例子
整数格的对偶格是其本身,也就是:
也就是整数格满足自对偶的性质。
如果把整数格的格点都扩大两倍,则形成子格。该格的对偶格则会出现小数,如下:
此处的系数有点类似倒数的感觉。
原始格的安全性在对偶格中依旧是存在的。
1.3 对偶格的图形理解
思考:给出任意一个向量点x,请找出所有跟这个向量点乘积为整数的点?
备注:向量与向量相乘为标量
线性代数告诉我们这些点会形成一个超平面,点跟点之间的距离为1/||x||。看一个二维的图形就很直接:
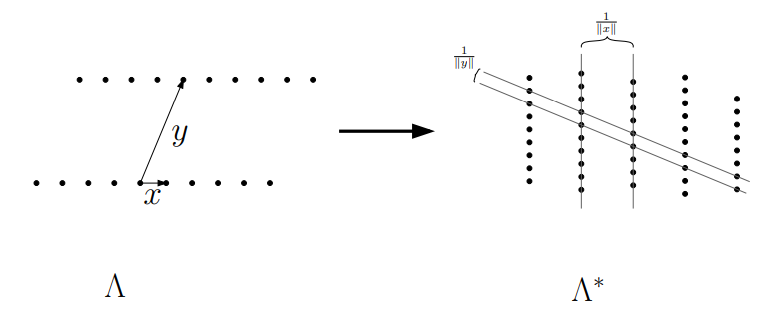
二. 对偶格的格基
格点相乘为整数,那这两个格的格基满足什么性质?
2.1 基本定义
原来的格基叫B,写做:
格基内每个向量都是m维,一共有n个向量。
对偶格的格基维度肯定是保持不变的,也就是:
对偶格和原来的格扩展空间肯定一致(向量点维度不一样的话,都不能相乘):
刚才发现对偶格有点倒数的感觉,反应在矩阵上则互逆,所以满足:
单位阵对角线上全为1,其他位置均为0。那么矩阵互逆告诉我们,向量位置一致时,相乘为1,也就是:
向量位置不一致时,相乘为0:
如果格基为方阵,也就是格满秩,则可以直接求逆,那么:
如果格基非方阵,也就是格非满秩,那么可以利用伪逆:
综合以上,对偶格的格基D需要满足两个性质:
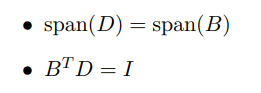
通过以上公式可以发现,只要B确定了,对偶格的格基D也是唯一确定的。
为什么格基满足如上性质,就可以是对偶格?请看2.2
2.2 对偶格的格基证明
本质就是需要证明:
借鉴集合相等的证明思路,我们的证明分成两步。
第一步:证明
从格L(B)内选取一个格点x,也就是,将其写做整数倍的向量求和形式:
从格基D中随机抽取一个向量,运算可得:
第一个等号:将格点x直接带入;
第二个等号:矩阵B与矩阵D互逆;
因为一定为整数,这个时候说明格基D中的每一个列向量都可以算做一个对偶格的格点。格点的求和运算具有封闭性,继续对这些对偶格点进行整数组合也一定是对偶格点,所以可得:
第二步:证明
从对偶格内随机取一个格点y,也就是:
根据对偶格的定义,易得:
根据扩展空间的定义,那么就可以将该点写做:
将对偶格的格点和原格的某个格基向量相乘,可得:
所以可得:
综上第一步和第二步,证明完毕。
三. 对偶格的行列式
对偶格的行列式与原来格的行列式互为倒数,也就是:
证明:
3.1 满秩格
将格基先转置在求逆,即为对偶格,所以可得:
逆矩阵的行列式与原矩阵的行列式互为倒数,所以可得:
矩阵转置不影响行列式的值,所以可得:
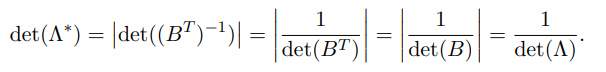
3.2 非满秩格
非满秩格不能直接求逆,则需要借助伪逆,运算性质与以上类似,可得:
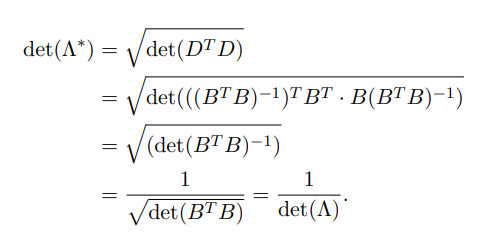
四. 重复对偶格
对偶格的对偶,即为原格,也就是:
证明:
考虑一般情况。记原格的格基为B,那么对偶格的格基为:
继续对格L(D)求对偶格,也就是运算:
带入运算可得:
![]()
五. 对偶格的转移定理(transference theorem)
本小节需要用到这篇博客的结论:
格密码与最短向量上界_最短向量问题-CSDN博客
假定格的秩为n,对偶格的最短向量长度满足:
证明:
首先根据闵可夫斯基上界(Minkowski's bound),可得:
![]()
将其类推到对偶格,可得:
![]()
两者相乘可得:
备注:根据Banaszczyk定理,这个界可以继续被放缩,可得:
六. 对偶格的连续最小值
本小节需要利用此篇博客的基础知识:
格密码基础:最短向量与连续最小值(附下界讨论)_格的逐次最小长度-CSDN博客
假定格的秩为n,可得:
证明:
假定v为原来的格最短的向量点,也就是:
从对偶格中取n个线性独立的向量:
根据格点相乘为整数,可得:
这两个向量的长度乘积必然大于1,也就是:
的长度一定比
要大,于是乎可得:
七. 对偶格的正交投影
对进行Gram-Schmidt正交化,可得:
其中代表将向量投影到前i-1个正交平面上,也就是:
假定B和D互为对偶格基。将矩阵B进行正交投影,可得:
此处就是把向量往同一个正交平面进行投影。
该格基的对偶格基与原来保持不变,也就是
证明:
从扩展平面角度来讲,可得:
根据对偶格基的性质。与
互相垂直,任意向量之间同样两两独立。换句话说,也就是:
所以可得:
满足对偶格基的第一个性质。
根据向量相乘的性质,不难计算:
![]()
根据逆矩阵的性质,不难证明原定理。
八. 对偶格基的正交化
原格基为:
Gram-Schmidt正交化为:
对偶格基:
按反方向,Gram-Schmidt正交化为:
长度满足:
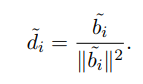
证明:通过以上对偶格基长度讨论易得。也可以用归纳法:
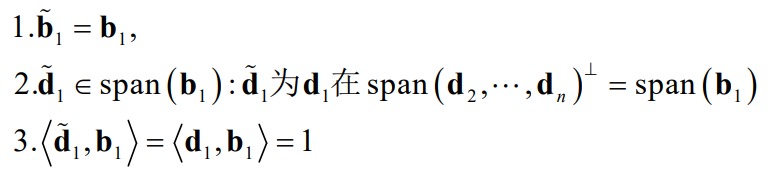


![[NSSRound#3 Team]This1sMysql](https://img-blog.csdnimg.cn/direct/2bb6b5bebe484ea4ae05473870405a13.png)
![[C#]利用opencvsharp实现深度学习caffe模型人脸检测](https://img-blog.csdnimg.cn/direct/9abd939faa5d437584fbbeff3a37e5e8.jpeg)