线性相关、基、维数

知识概要

​ 从线性相关或线性无关的特征入手，介绍空间的的几个重要概念：基、维数

线性无关与线性相关

（1）背景知识：

谈论的概念都是基于向量组的，而不是基于矩阵。线 性无关，线性相关是向量组内的关系，基也是一个向量组，不要与矩阵概念混淆。

首先从之前学习的 Ax = 0 方程谈起。

假设 m*n 的矩阵 A：

显然，n > m，以这样的矩阵 A 构成的方程 Ax = 0，此时未知数? ? 的个数比 方程的个数多。未知数一共 n 个，方程一共 m 个。

所以此时 A 的零空间中除零向量以外还有其他向量，原因是这样的 A 一定有 自由变量(至少有 n-m 个自由变量)，这就造成了零空间中向量的无穷解。

（2）线性无关与线性相关

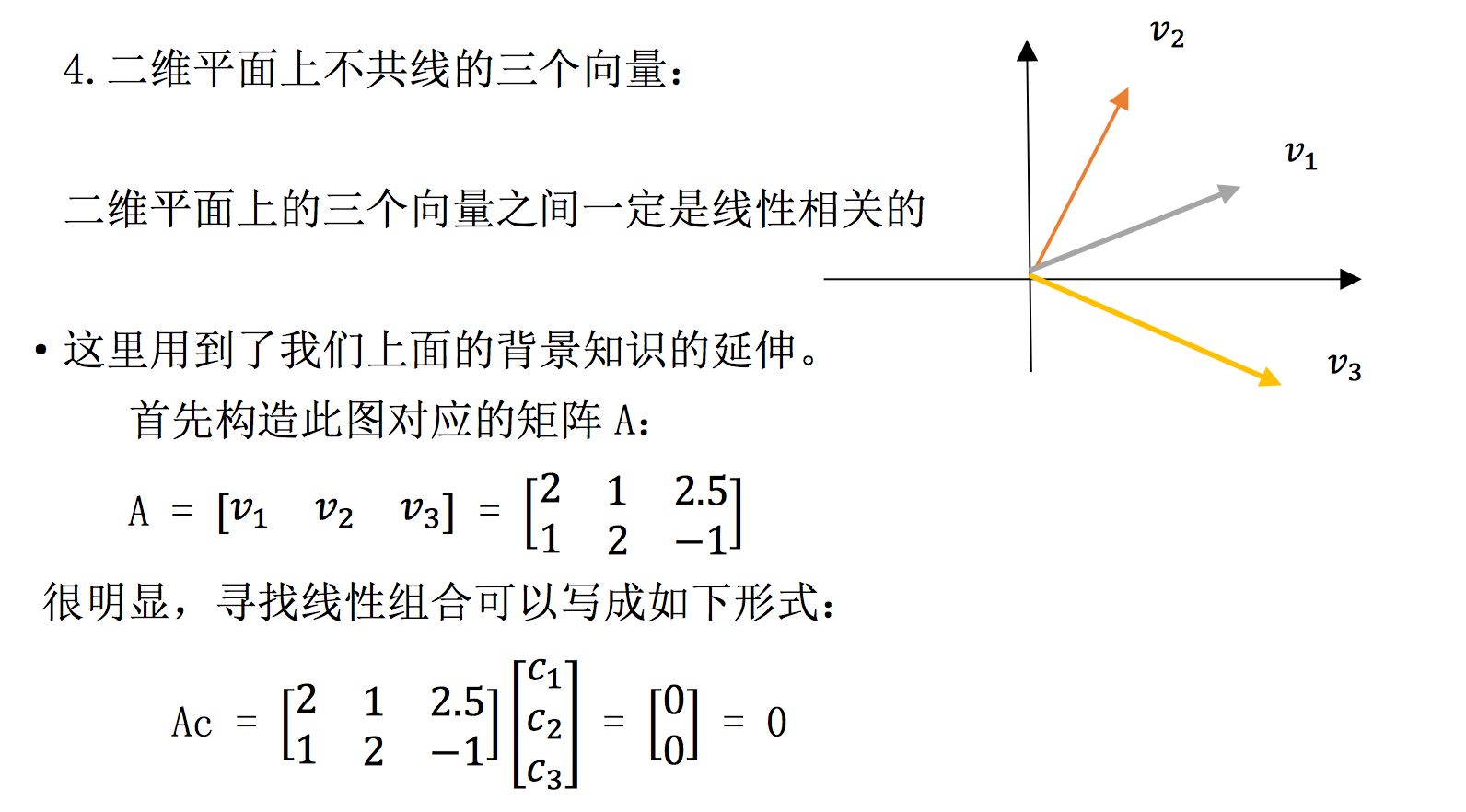
（3）零空间的作用

假设现有一 m*n 矩阵 A：

·如果 A 各列向量构成的向量组是线性无关的，那么矩阵 A 的零空间中只有零 向量。

·如果 A 各列向量构成的向量组是线性相关的，那么矩阵 A 零空间中除零向 量之外还一定有其他向量。

很好理解上面零空间角度的定义。因为零空间反映的就是 A 各列向量的线性 组合。

从秩的角度看来：

·线性无关对应向量组构成的矩阵，秩为 n，此时没有自由变量，零空间中 只有零向量存在。

·线性相关对应向量组构成的矩阵，秩小于 n，有 n-r 个自由变量，零空间 中有很多向量。

（4）生成空间

基

维数

理解维数也很简单，像我们的三维空间，其基一定是三个三维向量（三个 向量，每个向量有三个分量），四维空间的基也一定是四个四维向量。

总结

（2）找出A列空间的一个基

从 A 的结构看来：

列空间的维数，那么在这个列空间中随便找两个线性无关的向量，它们就可 以构成一组基，这组基就可以生成这个列空间。

（3)A对应零空间的维数为多少？

感悟

线性相关/无关，基，维数。这 一节这几个概念都是用来描述空间的，了解这几个概念之后，我们便将矩阵的秩， 矩阵的自由变量等概念与空间的维数，基，线性相关/无关的判定联系起来。