- 1.通过一个代码来了解矩阵乘法
- 2.基本快速幂
- 3.那么最后就是矩阵快速幂了
- 4.练习模板:
- 5.进阶运用,蓝桥杯15届省赛c语言组第9题
矩阵快速幂的学习流程:
- 矩阵乘法运算规则(线性代数基础)
- 快速幂的模板
1.通过一个代码来了解矩阵乘法
首先,先给出百度百科对于矩阵乘法的描述:
注意!!m x n表示m行n列

矩阵乘法的要点:
1.当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2.矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
3.乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
那么,根据这种描述,来写一个较为详细的小程序来模拟矩阵乘法:
#include<iostream>
#include<cstring>
#include<ctime>
#include<cstdlib>
using namespace std;
const int N = 1010;
int Matrix[N][N]; //存放最后的答案
int a[N][N]; //a,b分别是两个目标矩阵,a,b相乘得到Matrix
int b[N][N];
int row_a, row_b, col_a, col_b;
void Init(int (*a)[N],int (*b)[N]) //初始化
{
//step 1
//分别初始化a,b的行和列
//由于a的列要等于b的行,所有只需要初始化:
//(1)a的行 (2)a的列 (3)b的列
time_t t; //时间种子变量(必写)
srand((unsigned)time(&t)); //这句话必须写,当作模板背就好了。
//初始化a的行
row_a = rand() % 10;
while (!row_a) //不能为0
row_a = rand() % 10;
//初始化a的列
col_a = rand() % 10;
while (!col_a) //不能为0
col_a = rand() % 10;
//初始化b的列
col_b = rand() % 10;
while (!col_b)
col_b = rand() % 10;
//a的列要等于b的行
row_b = col_a;
//step 2
//初始化两个矩阵
for (int i = 1; i <= row_a; i++)
for (int j = 1; j <= col_a; j++)
a[i][j] = rand() % 20;
for (int i = 1; i <= row_b; i++)
for (int j = 1; j <= col_b; j++)
b[i][j] = rand() % 20;
}
void print(int(*a)[N],int n,int m) //输出
{
cout << "行n: " << n << " 列m: " << m << endl;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
printf("%-5d", a[i][j]); //左对齐
cout << endl;
}
cout << endl << endl;
}
void Mul(int (*a)[N],int (*b)[N],int n,int m,int p) //矩阵相乘
{
//建议根据博客的那个百度百科的图一起模拟
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 1; k <= p; k++)
Matrix[i][j] = Matrix[i][j] + a[i][k] * b[k][j];
}
int main()
{
cout << "模拟一下矩阵乘法,首先给两个矩阵(使用随机函数来生成两个矩阵):"<<endl;
Init(a, b);
print(a,row_a,col_a);
print(b,row_b,col_b);
//初始化完成,开始矩阵乘法
Mul(a,b,row_a,col_b,col_a);
cout << "答案:" << endl;
print(Matrix, row_a, col_b);
return 0;
}
运行:

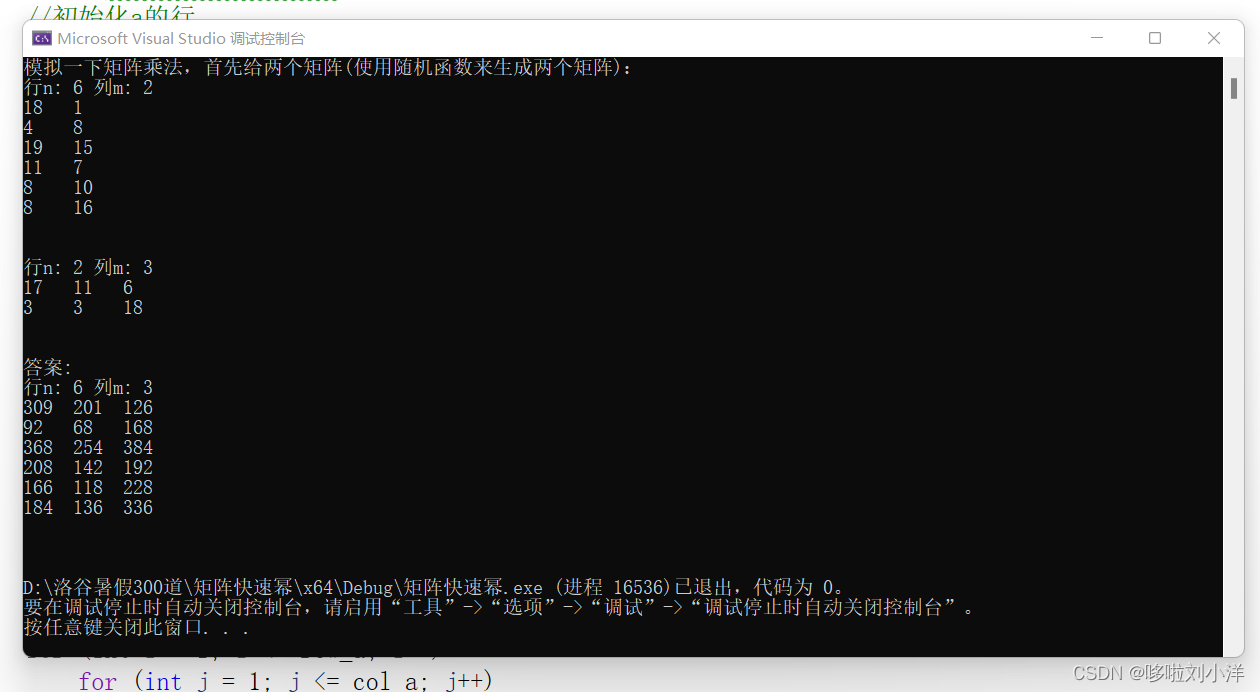
2.基本快速幂
快速幂图解:

#include<iostream>
using namespace std;
long long int ans=1;
int main()
{
int n;
cout << " 输入n,表示将要算出2的n次幂:\n";
cin >> n;
int k = 2;
while (n)
{
if ((n & 1)==1) //说明二进制位上是1
{
ans = ans * k;
}
k = k * k; //k*k相当于是2的幂次的乘2,因为二进制右移一位要乘2
n = n / 2;
}
cout << "ans=" << ans << endl;
return 0;
}

3.那么最后就是矩阵快速幂了
相当于把矩阵看成‘2’,然后算2n。当然实际上这个2是一个矩阵。换汤不换药哈。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<ctime>
using namespace std;
const int N = 101, mod = 1e9 + 7;
const int row = 10, col = 10; //这里默认矩阵的行列都是10,可以自己改,只是为了方便(默认n*n阶矩阵)
struct Matrix
{
long long int c[N][N];
Matrix() //默认构造函数
{
for (int i = 1; i <= N; i++) //初始化为单位矩阵
c[i][i] = 1;
}
};
Matrix A, B;
Matrix operator *(const Matrix& x, const Matrix& y) //重载运算符,不重载也行,但是为了使代码更加贴合快速幂模板,还是重载一下
{
Matrix temp;
for (int i = 1; i <= row; i++)
for (int j = 1; j <= col; j++)
temp.c[i][j] = 0;
for(int i=1;i<=row;i++)
for(int j=1;j<=col;j++)
for (int k = 1; k <= row;k++)
temp.c[i][j] = (temp.c[i][j] + x.c[i][k] * y.c[k][j]%mod)%mod; //取模,防止数据溢出
return temp;
}
void Init(Matrix& A) //初始化矩阵
{
time_t t;
srand((unsigned)time(&t));
for (int i = 1; i <= row; i++)
for (int j = 1; j <= col; j++)
A.c[i][j] = rand() % 20;
for (int i = 1; i <= row; i++)
{
for (int j = 1; j <= col; j++)
printf("%-5d", A.c[i][j]);
cout << endl;
}
}
void kuaisumi(Matrix& A,Matrix& B,int n) //写一个快速幂的模板即可
{
while (n)
{
if ((n & 1) == 1)
B = B * A;
A = A * A;
n /= 2;
}
}
int main()
{
int n;
cout << "随机初始化一个矩阵:"<<endl;
Init(A); //随机初始化一个矩阵
cout << "接下来,计算矩阵A的n次幂:" << endl;
cout << "请输入n:";
cin >> n;
cout << "最终矩阵:"<<endl;
kuaisumi(A,B,n);
for (int i = 1; i <= row; i++)
{
for (int j = 1; j <= col; j++)
printf("%-10d", B.c[i][j]);
cout << endl;
}
return 0;
}
4.练习模板:
矩阵快速幂点这里
代码:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110,mod=1e9+7;
long long int n, m;
struct Matrix
{
long long int c[N][N];
}A,B;
Matrix operator*(const Matrix& A, const Matrix& B)
{
Matrix temp;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
temp.c[i][j] = 0;
for(int i=1;i<=n;i++)
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
temp.c[i][j] = (temp.c[i][j] + A.c[i][k] * B.c[k][j] % mod)%mod;
}
return temp;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
cin >> A.c[i][j];
for (int i = 1; i <= n; i++)
B.c[i][i] = 1;
while (m>0)
{
if (m % 2 == 1)
B = B * A;
A = A * A;
m /= 2;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
cout << B.c[i][j] << " ";
cout << endl;
}
return 0;
}
5.进阶运用,蓝桥杯15届省赛c语言组第9题
这题难,自己写不出来,贴个链接垒骰子