实验要求

使用M4核开发
PF7/PF8/PF9/PF5/PF12/PE15检测中断
要求1：当中断到来时，LED灯状态取反
要求2：当中断触发时，打印一句话
例如按键1触发，LED1状态取反，串口打印一句话：KEY1 DOWN#####

MX相关设置

LED设置

以LED1为例：
1、选择模式为GPIO_Output

2、鼠标右键选择M4核

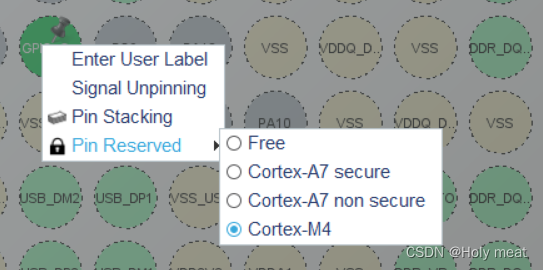
3、配置信息

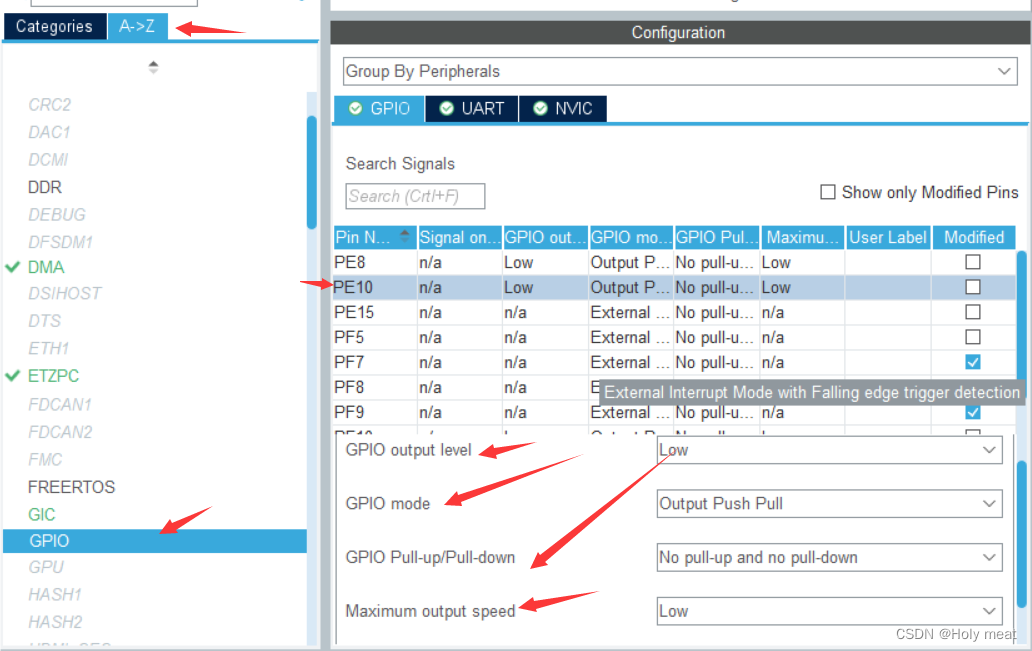
按键设置

以KEY1为例：
1、鼠标左键选择GPIO_EXTI9

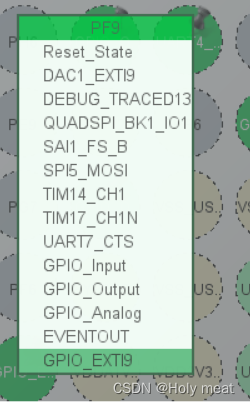
2、鼠标右键选择M4核

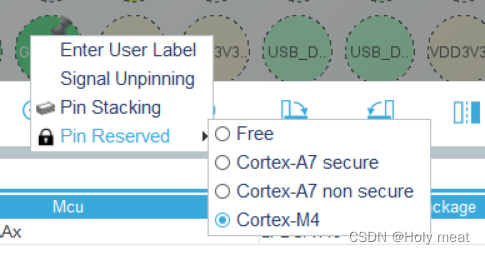
3、配置信息，选择下降沿触发

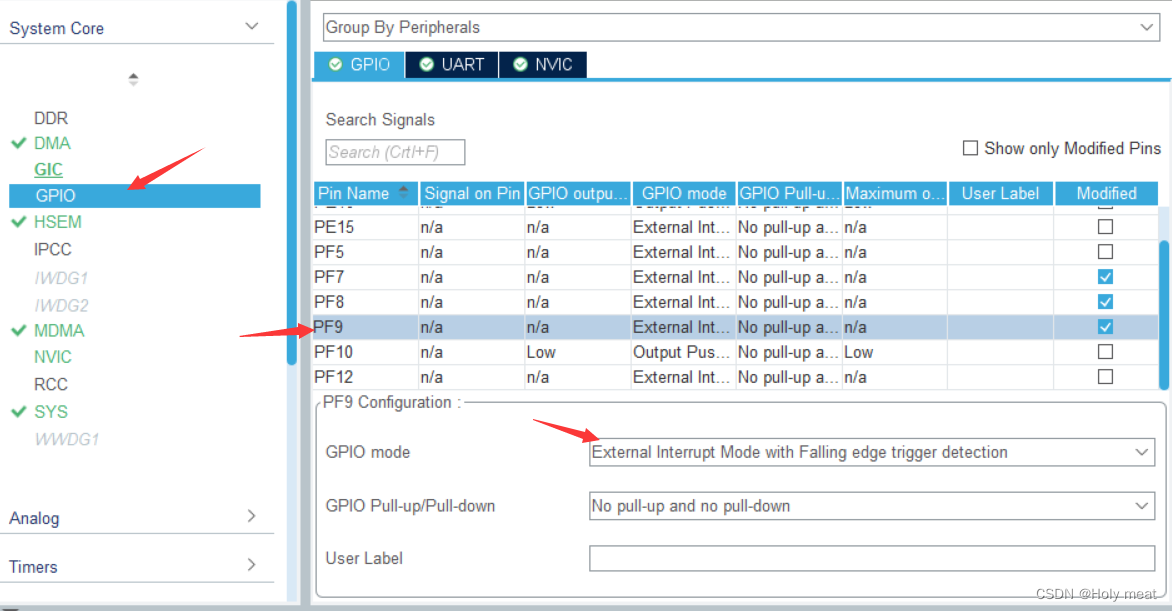
4、设置NVIC，使其使能，并设置优先级

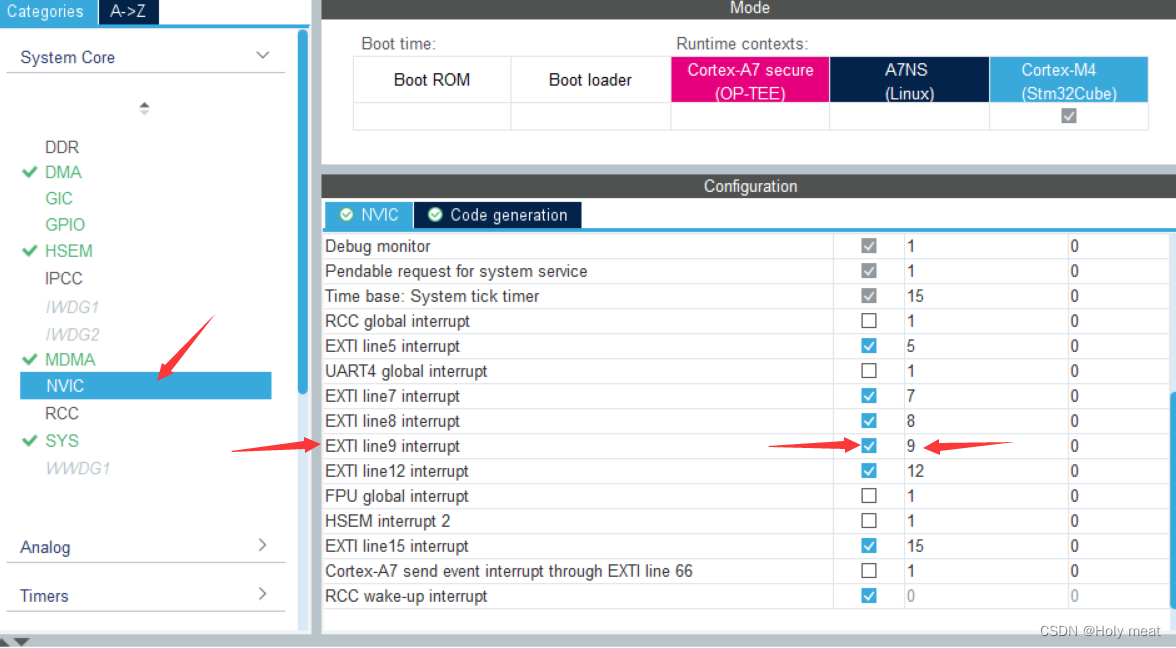
光电开关，火焰传感器，人体红外设置

同按键中断

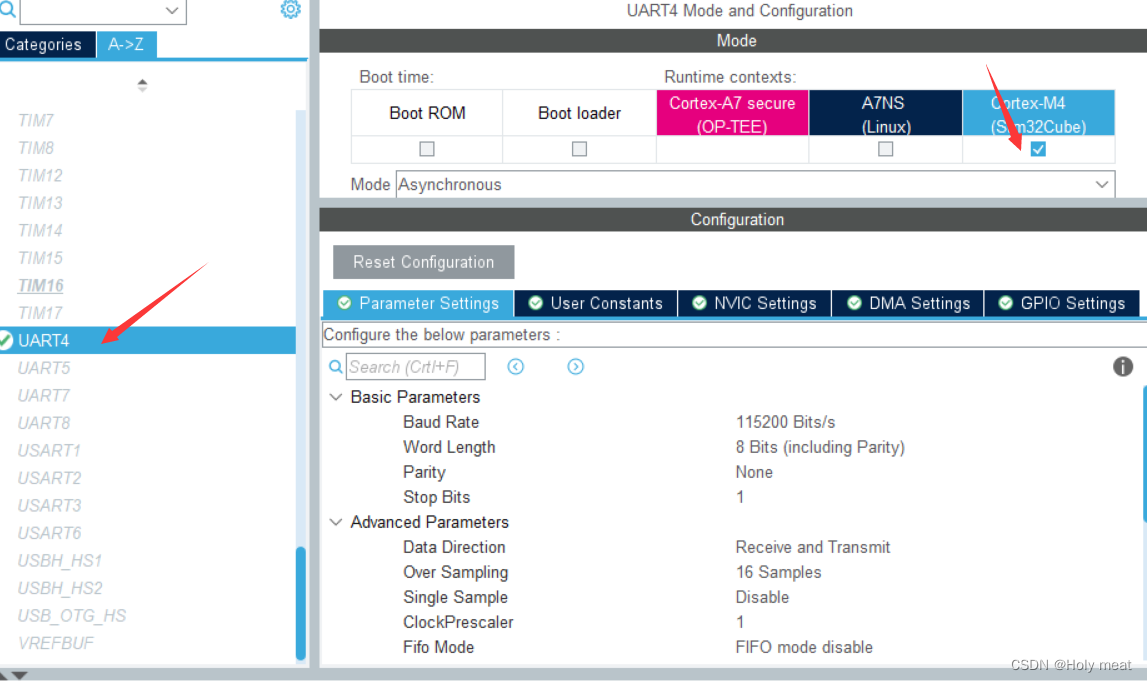
UART4设置

PB2
1、鼠标左键选择UART4_RX

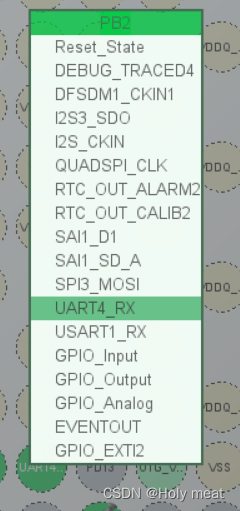
PG11
1、鼠标左键选择UART4_TX

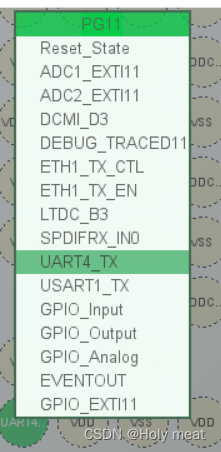
2、选择M4核

代码编写

1、gpio.c 部分关键代码

void HAL_GPIO_EXTI_Falling_Callback(uint16_t GPIO_Pin)
{
	switch(GPIO_Pin)
	{
		/*KEY-----LED2*/
		case GPIO_PIN_7:
			HAL_GPIO_TogglePin(GPIOF,GPIO_PIN_10);
			printf("LED2 DOWN !!!");
			break;
		case GPIO_PIN_8:
			HAL_GPIO_TogglePin(GPIOE,GPIO_PIN_10);
		  printf("LED1 DOWN !!!");
			break;
		case GPIO_PIN_9:
			HAL_GPIO_TogglePin(GPIOE,GPIO_PIN_8);
			printf("LED3 DOWN !!!");
			break;		
	}
}

void HAL_GPIO_EXTI_Rising_Callback(uint16_t GPIO_Pin)
{
	switch(GPIO_Pin)
	{
		case GPIO_PIN_15:
			HAL_GPIO_TogglePin(GPIOF,GPIO_PIN_10);
			printf("LED2 DOWN !!!");
			break;
		case GPIO_PIN_5:
			HAL_GPIO_TogglePin(GPIOE,GPIO_PIN_10);
			printf("LED1 DOWN !!!");
			break;
		case GPIO_PIN_12:
			HAL_GPIO_TogglePin(GPIOF,GPIO_PIN_8);
			printf("LED3 DOWN !!!");
			break;
		
	}
}

2、uart.c 部分代码

int fputc(int ch,FILE* stream)
{
	while(!(huart4.Instance->ISR & (0x1 << 7)));
	huart4.Instance->TDR = ch;
	if(ch == '\n')
	{
		while(!(huart4.Instance->ISR & (0x1 << 7)));
		huart4.Instance->TDR = '\r';
		
	}
	return ch;
}

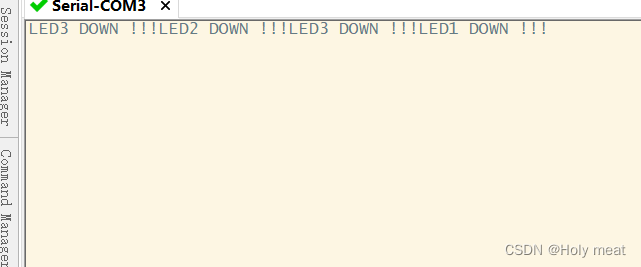
结果测试