基本原理

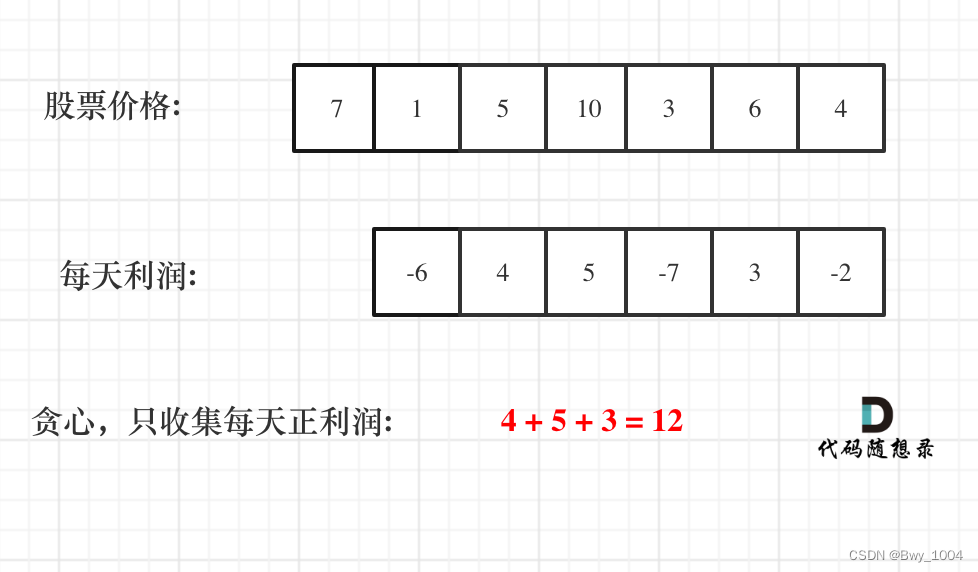
凡聚类者，必有中心。按照这个思路，如果某个区域满足聚类的要求，那么其自然中心与样本均值应该是几乎重合的，这也是MeanShift算法的基本逻辑。

假设现有100个点，然后随机选择1个聚类中心，统计距离这个聚类中心$r$以内的点的平均值

import numpy as np
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=100)
cTest = [2,2]

def updateCenter(X, cTest):
    d = np.linalg.norm(X - cTest, axis=1)
    return np.mean(X[d<3], axis=0)  # 半径设为3

cNew = updateCenter(X, cTest)
print(cNew)
# [2.84336857 0.00494472]

其中，X, y = make_blobs(n_samples=100)用于创建一个涵盖100个点的聚类测试点集，其中X为点的坐标集合，y为点的label集合。

updateCenter函数是MeanShift算法的核心函数，表示求取当前聚类中心和聚类点之间距离的平均值。

cNew是进行一次updateCenter之后的聚类点集。接下来，可以把updateCenter前后的聚类中心绘制出来

def drawMS(X, r, cNew, cOld=[0,0]):
    plt.scatter(X[:,0], X[:,1], marker='.')     # 样本点
    plt.scatter(cOld[0], cOld[1], marker='o')   # 预设中心
    plt.scatter(cNew[0], cNew[1], marker='*')   # 样本均值
    th = np.linspace(0, np.pi*2, 100)
    xs = r * np.cos(th) + cOld[0]
    ys = r * np.sin(th) + cOld[1]
    plt.plot(xs, ys)
    plt.show()

drawMS(X, 3, cNew)

得到结果如下，其中绿色的星星表示满足样本要求的点的平均值，

接下来再以cNew为中心画圆，重复刚才的操作

cOld = cNew
cNew = updateCenter(X, cOld)
drawMS(X, 3, cNew, cOld)

效果为

可以非常明显地看到，这个大圆和圆心（五角星）都向着更密集的点的方向靠拢。随着迭代算法的不断进行，大圆的圆心早晚会和这些点的质心重合在一起，从而完成聚类。

sklearn调用

一般来说，越是靠近聚类中心的地方，样本应该越密集，越是远离聚类中心，则样本越稀疏。换言之，越是靠近中心的地方，理应享有更大的权重，所以在sklearn中，采用的斌不是直接求样本均值，而是采用样本加权平均值，可表示为

$$N(x)=\frac{1}{\sqrt{2\pi }h}{e}^{-\frac{-x^2}{2h^2}}$$

其中h为带宽，起到类似半径的限制作用。在sklearn中提供的MeanShift类，其构造函数中最重要的参数就是带宽bandwidth。

最后，测试一下MeanShift

from sklearn.cluster import MeanShift
ms = MeanShift(bandwidth=3)
ms.fit(X)
plt.scatter(X[:,0], X[:,1], c=ms.labels_)
plt.show()

效果如下，可见MeanShift算法对样本的分类是符合人类直觉的，X被分成了三类，每一类都标上了不同的颜色。