向量链式求导法则
标量链式法则:
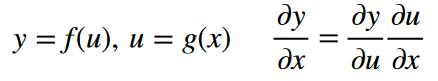
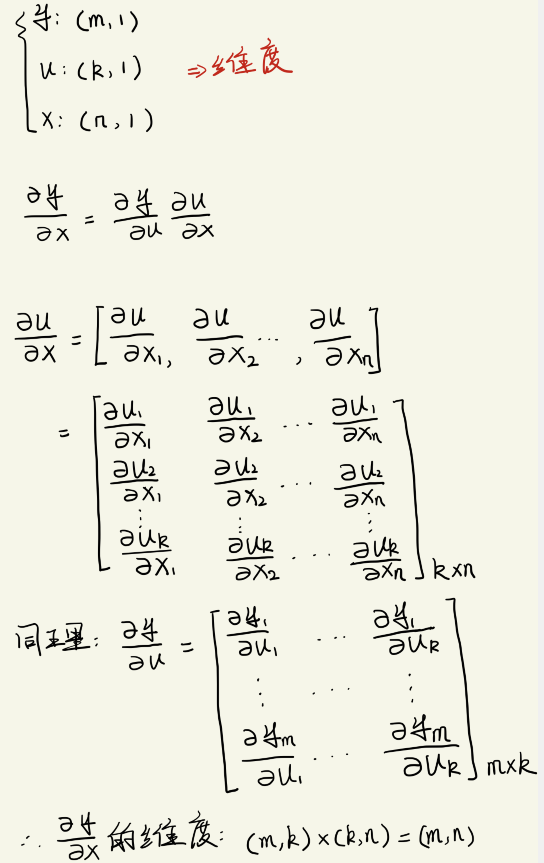
扩展到向量:
-
y y y是关于标量 u u u的一个标量, x \bf{x} x是一个向量
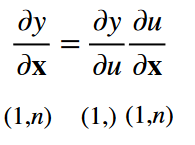
-
y y y是关于向量 u \bf{u} u的一个标量, x \bf{x} x是一个向量
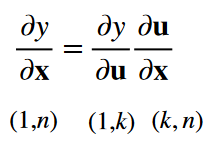
-
y \bf{y} y是关于向量 u \bf{u} u的一个向量, x \bf{x} x是一个向量
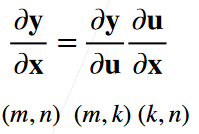
实例1:

实例2:

计算图
- 将代码分解成操作子
- 将计算表示成一个无环图
如:
z
=
(
⟨
x
,
w
⟩
−
y
)
2
z = (⟨x, w⟩ − y)^2
z=(⟨x,w⟩−y)2表示成下面的无环图:

该图就是一个计算图
计算图由两种构造方式:
-
显示构造:(tensorflow/Theano/MXNet)
先将公式构造出来,最后再赋值

-
隐式构造:(PyTorch/MXNet)
先赋值,再构造公式

自动求导的两种模式
对于链式求导:

可以从前往后计算,也可以从后往前计算,如下所示:

反向积累:正是模型训练过程反向传播,上面的 y y y相当于 l o s s loss loss,从后面向前传播梯度。
在实际中,会先正向计算并存储中间变量的值。
如下图,在正向中会计算
w
、
x
、
y
、
a
、
b
、
z
w、x、y、a、b、z
w、x、y、a、b、z的值

在反向积累计算导数的时候,就会用到正向传播过程中存储的中间变量:

反向累计求导复杂度:
计算复杂度为
O
(
n
)
O(n)
O(n),
n
n
n为操作子的个数;内存代价也为
O
(
n
)
O(n)
O(n),因为需要存储
n
n
n各操作子的值。