🍨 本文为🔗365天深度学习训练营中的学习记录博客
🍦 参考文章：第R2周：LSTM-火灾温度预测（训练营内部可读）
🍖 作者：K同学啊

任务说明：数据集中提供了火灾温度（Tem1）、一氧化碳浓度（CO 1）、烟雾浓度（Soot 1）随着时间变化数据，我们需要根据这些数据对未来某一时刻的火灾温度做出预测（本次任务仅供学习）

🍺要求：
1了解LSTM是什么，并使用其构建一个完整的程序
2R2达到0.83

🍻拔高：
1使用第1~8个时刻的数据预测第9~10个时刻的温度数据

一句话介绍LSTM，它是RNN的进阶版，如果说RNN的最大限度是理解一句话，那么LSTM的最大限度则是理解一段话，详细介绍如下：
LSTM，全称为长短期记忆网络(Long Short Term Memory networks)，是一种特殊的RNN，能够学习到长期依赖关系。LSTM由Hochreiter & Schmidhuber (1997)提出，许多研究者进行了一系列的工作对其改进并使之发扬光大。LSTM在许多问题上效果非常好，现在被广泛使用。
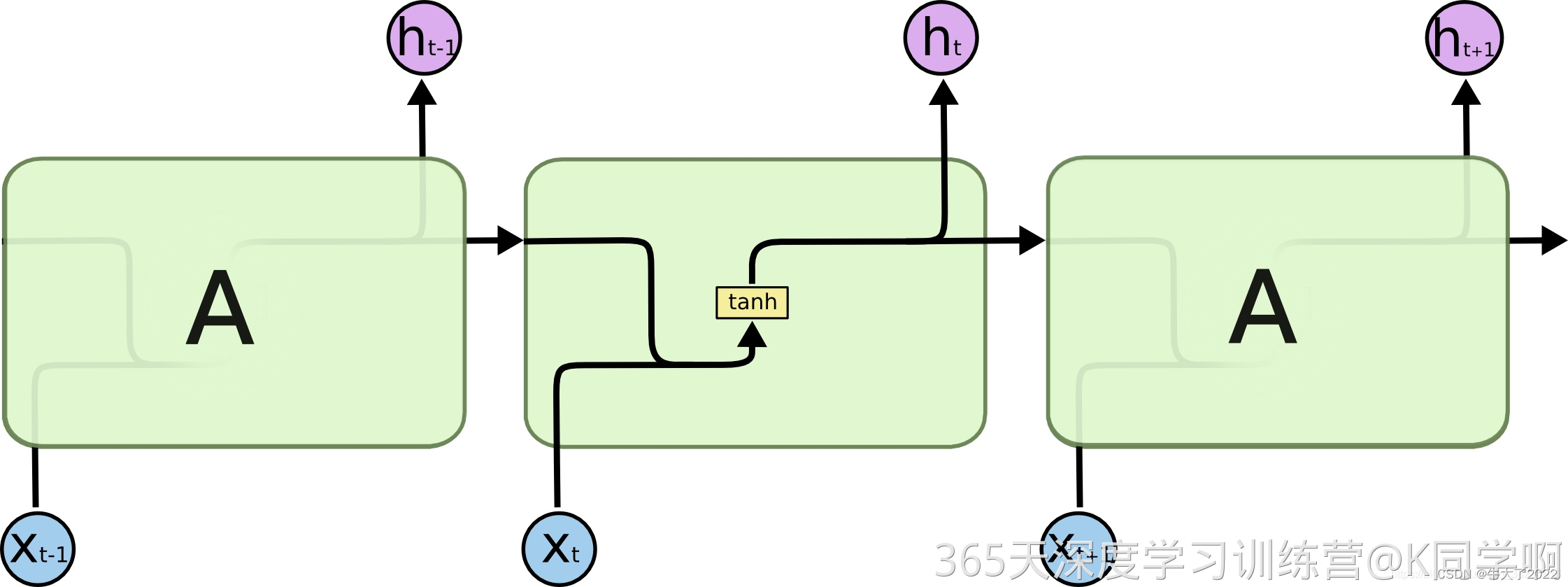
所有的循环神经网络都有着重复的神经网络模块形成链的形式。在普通的RNN中，重复模块结构非常简单，其结构如下：

LSTM避免了长期依赖的问题。可以记住长期信息！LSTM内部有较为复杂的结构。能通过门控状态来选择调整传输的信息，记住需要长时间记忆的信息，忘记不重要的信息，其结构如下：

一.前期准备工作

1.导入数据

数据地址：🔗百度网盘

import tensorflow as tf
import pandas     as pd
import numpy      as np

gpus = tf.config.list_physical_devices("GPU")
if gpus:
    tf.config.experimental.set_memory_growth(gpus[0], True)  #设置GPU显存用量按需使用
    tf.config.set_visible_devices([gpus[0]],"GPU")
print(gpus)

[PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')]

顺便先导入数据

df_1 = pd.read_csv("woodpine2.csv")
df_1.head()

2.数据可视化

import matplotlib.pyplot as plt
import seaborn as sns

plt.rcParams['savefig.dpi'] = 500 #图片像素
plt.rcParams['figure.dpi']  = 500 #分辨率

fig, ax =plt.subplots(1,3,constrained_layout=True, figsize=(14, 3))

sns.lineplot(data=df_1["Tem1"], ax=ax[0])
sns.lineplot(data=df_1["CO 1"], ax=ax[1])
sns.lineplot(data=df_1["Soot 1"], ax=ax[2])
plt.show()

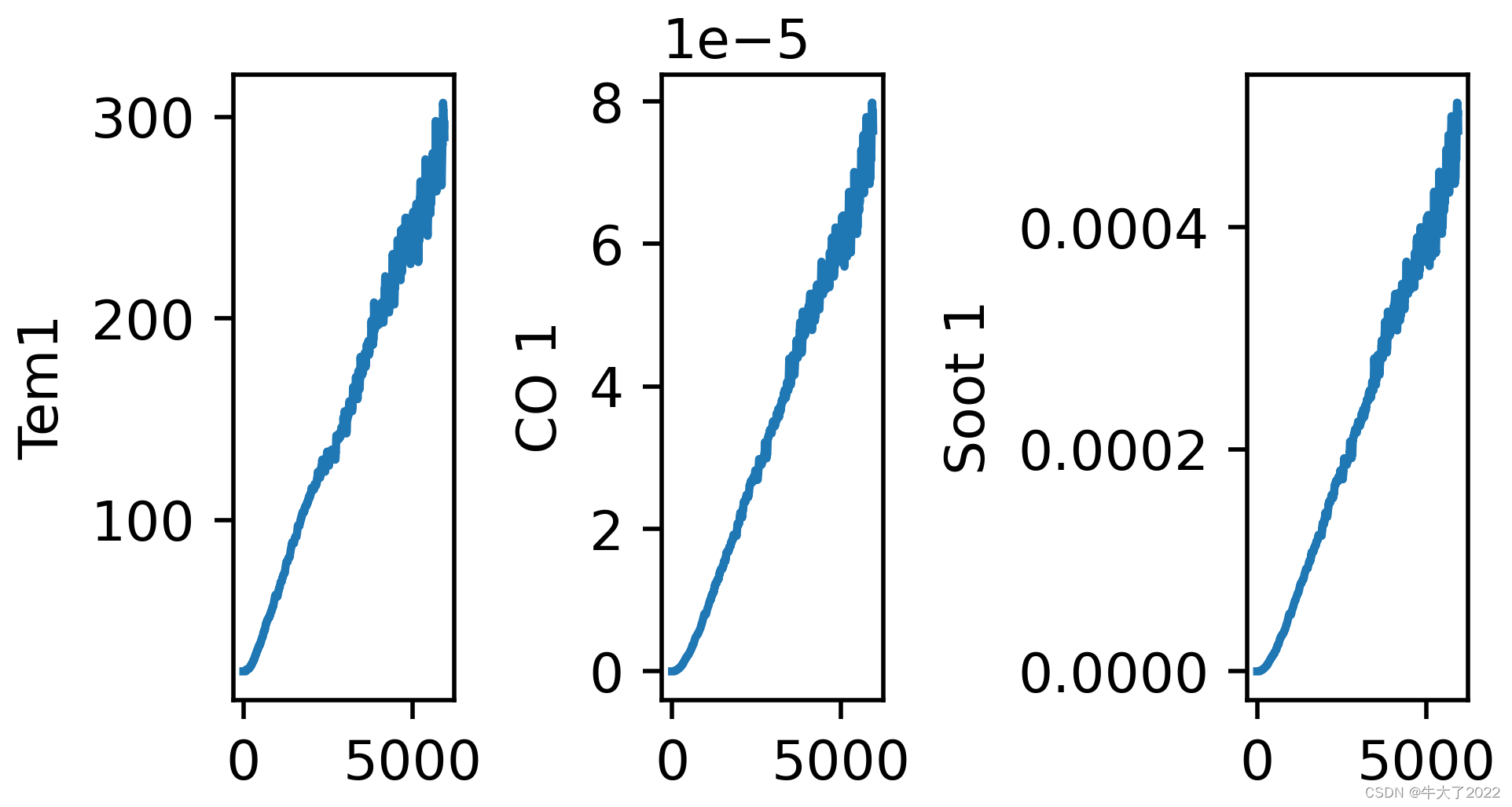
二、构建数据集

dataFrame=df_1.iloc[:,1:]
print(dataFrame)

1.设置X,y

width_X=8
width_y=2

取前8个时间段的Tem1、CO 1、Soot 1为X，而第9,10个时间段的Tem1为y。

X = []
y = []

in_start = 0

for _, _ in df_1.iterrows():
    in_end = in_start + width_X
    out_end = in_end + width_y

    if out_end < len(dataFrame):
        X_ = np.array(dataFrame.iloc[in_start:in_end, ])

        X_ = X_.reshape((len(X_) * 3))
        y_ = np.array(dataFrame.iloc[in_end:out_end, 0])

        X.append(X_)
        y.append(y_)

    in_start += 1

X = np.array(X)
y = np.array(y)

print(X.shape, y.shape)

((5938, 24), (5938, 2))

2.归一化

from sklearn.preprocessing import MinMaxScaler

#将数据归一化，范围是0到1
sc       = MinMaxScaler(feature_range=(0, 1))
X_scaled = sc.fit_transform(X)
X_scaled.shape

(5939, 24)

X_scaled=X_scaled.reshape(len(X_scaled),width_X,3)
X_scaled.shape

(5938, 8, 3)

3.划分数据集

取5000之前的数据为训练集，5000之后的为验证集

X_train=X_scaled[:5000]
y_train=y[:5000]

X_test=X_scaled[5000:,]
y_test=y[5000:,]

X_train.shape

(5000, 8, 3)

三.构建模型

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense,LSTM,Bidirectional
from tensorflow.keras        import Input

model_lstm = Sequential()
model_lstm.add(LSTM(units=64, activation='relu', return_sequences=True,
               input_shape=(X_train.shape[1], 3)))
model_lstm.add(LSTM(units=64, activation='relu'))

model_lstm.add(Dense(width_y))

WARNING:tensorflow:Layer lstm_8 will not use cuDNN kernel since it doesn't meet the cuDNN kernel criteria. It will use generic GPU kernel as fallback when running on GPU
WARNING:tensorflow:Layer lstm_9 will not use cuDNN kernel since it doesn't meet the cuDNN kernel criteria. It will use generic GPU kernel as fallback when running on GPU

四.模型训练

1.模型编译

#只观察loss数值，不观察准确率，所以删去metrics选项
model_lstm.compile(optimizer=tf.keras.optimizers.Adam(1e-3),
                  loss='mean_squared_error')

from tensorflow.keras.callbacks import ModelCheckpoint

ModelCheckPointer=ModelCheckpoint('best_model.h5',
                                  monitor='val_loss',
                                  save_best_only=True,
                                  save_weights_only=True,               
                )

print(X_train.shape,y_train.shape)

(5000, 8, 3) (5000, 2)

history_lstm=model_lstm.fit(X_train,y_train,
                            batch_size=64,
                            epochs=50,
                            validation_data=(X_test,y_test),
                            validation_freq=1,
                            callbacks=[ModelCheckPointer])

然后就是训练了。和以前训练差不多，不在赘述。

五.评估

1.loss图

# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

plt.figure(figsize=(5, 3),dpi=120)

plt.plot(history_lstm.history['loss']    , label='LSTM Training Loss')
plt.plot(history_lstm.history['val_loss'], label='LSTM Validation Loss')

plt.title('Training and Validation Loss')
plt.legend()
plt.show()

2.调用方模型进行预测

model_lstm.load_weights('best_model.h5')

predicted_y_lstm=model_lstm.predict(X_test)

y_test_one=[i[0] for i in y_test]
predicted_y_lstm_one=[i[0] for i in predicted_y_lstm]

y_test_two=[i[1] for i in y_test]
predicted_y_lstm_two=[i[1] for i in predicted_y_lstm]


fig, ax =plt.subplots(1,2,constrained_layout=True, figsize=(14, 3))
#画出第9个时间段真实数据与预测数据的对比图
ax[0].plot(y_test_one[:1000],color='red',label='真实值')
ax[0].plot(predicted_y_lstm_one[:1000],color='blue',label='预测值')

#画出第10个时间段真实数据与预测数据的对比图
ax[1].plot(y_test_two[:1000],color='red',label='真实值')
ax[1].plot(predicted_y_lstm_two[:1000],color='blue',label='预测值')

ax[0].set(xlabel='X',ylabel='Y',title='第9个时间段')
ax[1].set(xlabel='X',ylabel='Y',title='第10个时间段')

from sklearn import metrics
"""
RMSE ：均方根误差  ----->  对均方误差开方
R2   ：决定系数，可以简单理解为反映模型拟合优度的重要的统计量
"""
RMSE_lstm  = metrics.mean_squared_error(predicted_y_lstm, y_test)**0.5
R2_lstm    = metrics.r2_score(predicted_y_lstm, y_test)

print('均方根误差: %.5f' % RMSE_lstm)
print('R2: %.5f' % R2_lstm)