题目描述

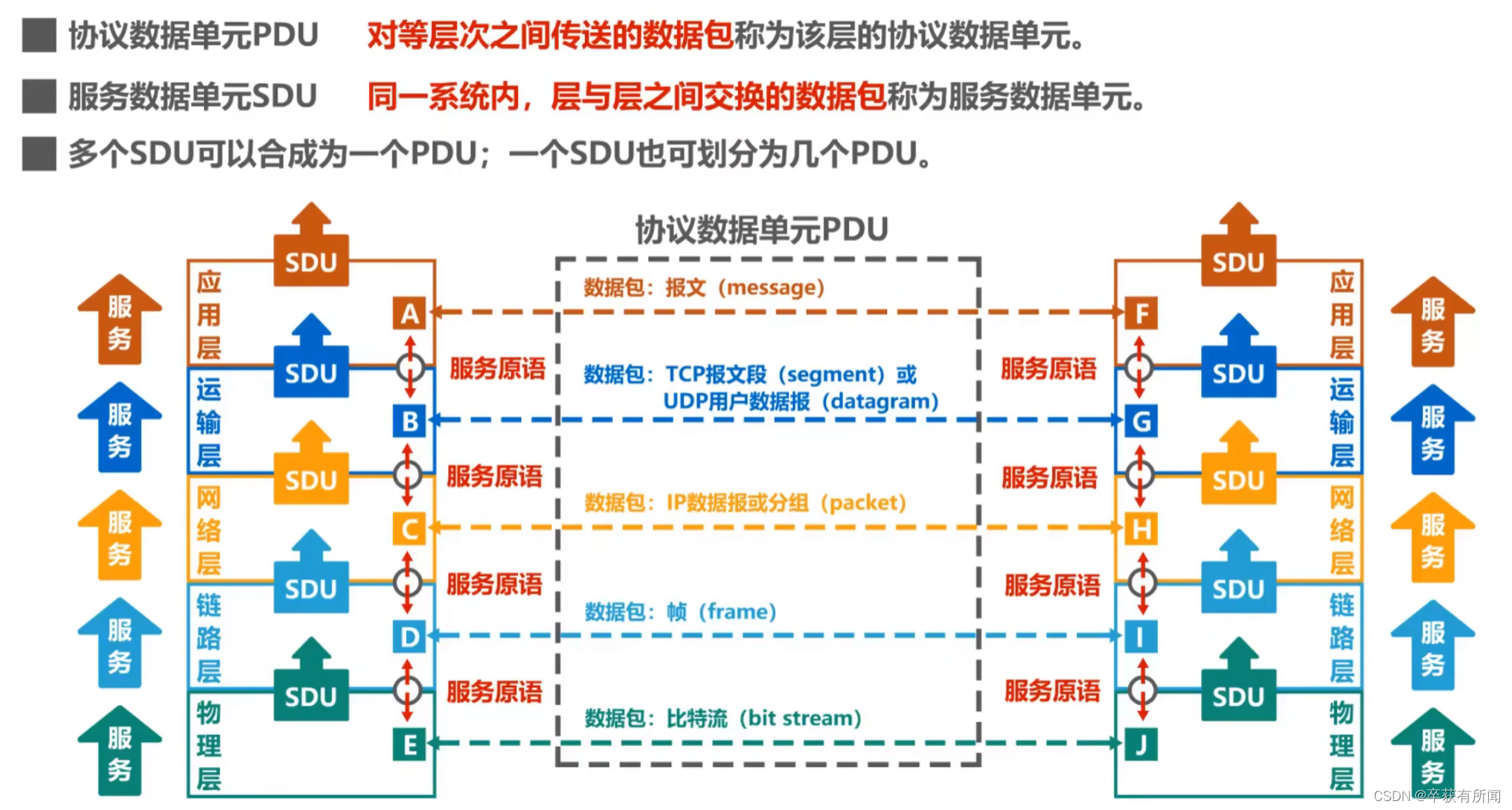
农夫约翰非常认真地对待他的奶牛们的血统。然而他不是一个真正优秀的记帐员。他把他的奶牛 们的家谱作成二叉树，并且把二叉树以更线性的“树的中序遍历”和“树的前序遍历”的符号加以记录而 不是用图形的方法。

你的任务是在被给予奶牛家谱的“树中序遍历”和“树前序遍历”的符号后，创建奶牛家谱的“树的 后序遍历”的符号。每一头奶牛的姓名被译为一个唯一的字母。（你可能已经知道你可以在知道树的两 种遍历以后可以经常地重建这棵树。）显然，这里的树不会有多于 26 个的顶点。 这是在样例输入和 样例输出中的树的图形表达方式：

　　　　　　　　 C
　　　　　　   /  \
　　　　　　  /　　\
　　　　　　 B　　  G
　　　　　　/ \　　/
　　　　   A   D  H
　　　　　　  / \
　　　　　　 E   F

树的中序遍历是按照左子树，根，右子树的顺序访问节点。

树的前序遍历是按照根，左子树，右子树的顺序访问节点。

树的后序遍历是按照左子树，右子树，根的顺序访问节点。

输入格式

第一行： 树的中序遍历

第二行： 同样的树的前序遍历

输出格式

单独的一行表示该树的后序遍历。

输入输出样例

输入 #1复制

ABEDFCHG
CBADEFGH 

输出 #1复制

AEFDBHGC

说明/提示

题目翻译来自NOCOW。

USACO Training Section 3.4

1.这一题牵扯到的知识是二叉树。

 2.我们根据中序遍历的特点，在根节点左边是左子树，在根节点右边的右子树。而前序遍历出现在前面的都是根节点。我们需要根据这个特点去写。

3.前序的根节点，在中序里面刚好可以把他们分为左右子树。 

我们再分别递归前部分和后部分。

我们在接下来的前序遍历中需要找到，第一个在前序遍历里面，然后它在中序遍历是又可以分为左右子树的。

4.我们在递归变小的时候，因为后序节点是左右根，而递归刚好又是先进后出的原则，我们可以写成fun(左子树)，fun(右子树)，最后printf("%c",根节点)；即可

代码如下：

#include<stdio.h>
#include<string.h>
char zx[30],xx[30],n;
char fun(int left,int right)
{
	int i,j;
	if(left>right) return 0;
	for(i=0;i<n;i++)
	{
		for(j=left;j<=right;j++)
		{
			if(xx[i]==zx[j]) break;
		}
		if(j<=right) break;
	}
	fun(left,j-1);
	fun(j+1,right);
	printf("%c",zx[j]);
}
int main()
{
	scanf("%s%s",zx,xx);
	n=strlen(zx);
	fun(0,n-1);
	return 0;
}