问题描述

原题链接🔗：756. 蛇形矩阵

输入两个整数 $n$ 和 $m$，输出一个 $n$ 行 $m$ 列的矩阵，将数字 $1$ 到 $n\times m$ 按照回字蛇形填充至矩阵中。

具体矩阵形式可参考样例。

输入格式
输入共一行，包含两个整数 $n$ 和 $m$。

输出格式
输出满足要求的矩阵。

矩阵占 $n$ 行，每行包含 $m$ 个空格隔开的整数。

数据范围
$1\le n,m\le 100$

输入样例：

3 3

输出样例：

1 2 3
8 9 4
7 6 5

思路与代码

1. 个人解法

观察题目不难发现，填充方向为顺时针并且是一圈一圈往内填的，如下图所示：

填完红圈之后，开始填蓝圈，最后填绿圈，当发现填完的数字等于 $n\cdot m$ 后，结束填充。

无论是哪种颜色的圈，当位于上边界的时候，移动方向总是向右的；当位于右边界的时候，移动方向总是向下的；当位于下边界的时候，移动方向总是向左的；当位于左边界的时候，移动方向总是向上的。

以最外圈（红圈）为例，我们可以将其划分成四个区域：

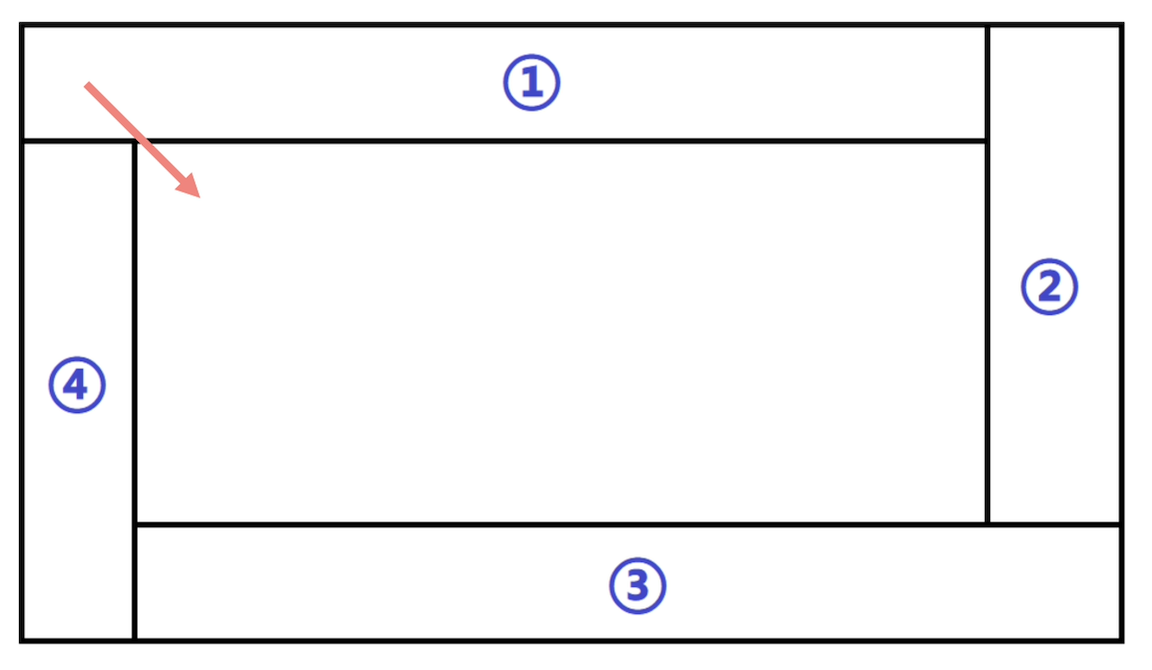
区域1上的点满足 $i=0,j<m-1$，且在该区域上向右移动；区域2上的点满足 $i<n-1,j=m-1$，且在该区域上向下移动；区域3上的点满足 $i=n-1,j>0$，且在该区域上向左移动；区域4上的点满足 $i>0,j=0$，且在该区域上向上移动。

当填充完外圈后，我们如何进入内圈呢？很简单，只需要将数组进行全0初始化，如果一圈还没有填充完，则下一个填充位置必然为0，如果刚好填完了一圈，则下一个填充位置必不为0。以红圈为例，当填充完该圈后，下一个填充位置为区域1的第一个方格处，即 $i=0,j=0$，此时我们需要对其矫正，即执行 i++, j++（对应上图中的红色箭头），这样一来，下一个填充位置就变成内圈的起始处（$i=1,j=1$）。

在内圈上移动时，我们需要缩减边界，可以理解为“缩圈”，此时四个区域上的点满足：
$$\begin{array}{rl}& {\text{region}}_1:i=1,j<m-2\\ & {\text{region}}_2:i<n-2,j=m-2\\ & {\text{region}}_3:i=n-2,j>1\\ & {\text{region}}_4:i>1,j=1\end{array}$$

填充结束当且仅当刚刚填充的数字为 $n\cdot m$。

AC代码：

#include <iostream>

using namespace std;

int a[100][100];  // 全局变量自动初始化为0

int main() {
    int n, m;
    cin >> n >> m;
    int bound[] = {0, n - 1, 0, m - 1};  // 分别对应上、下、左、右边界

    for (int i = 0, j = 0, k = 1; k <= n * m; k++) {
        a[i][j] = k;
        if (k == n * m) break;  // 填充结束

        // 否则，移动到下一个填充位置
        if (i == bound[0] && j < bound[3]) j++;
        else if (i < bound[1] && j == bound[3]) i++;
        else if (i == bound[1] && j > bound[2]) j--;
        else if (i > bound[0] && j == bound[2]) i--;

        // 如果下一个填充位置已经填过了，则说明此时已经填完一圈了，此时应当缩小边界
        if (a[i][j]) {
            i++, j++;  // 矫正新的一圈的起始位置
            bound[0]++, bound[1]--, bound[2]++, bound[3]--;  // 缩圈
        }
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++)
            cout << a[i][j] << " ";
        cout << endl;
    }

    return 0;
}

2. 官方题解

考虑使用方向数组。

因为在填充过程中移动方向只有四种：上、下、左、右，所以方向数组的大小为 $4$。设某一方格的坐标（准确来讲应当是索引）为 $(x,y)$，则其上、下、左、右四个方格的坐标分别为 $(x-1,y),(x+1,y),(x,y-1),(x,y+1)$，由此可得到上、下、左、右这四个方向分别为 $(-1,0),(1,0),(0,-1),(0,1)$。

例如当前坐标为 $(x,y)$，向左移动一步后得到 $(x^{\prime },y^{\prime })$，则坐标更新公式为

$$(x^{\prime },y^{\prime })=(x,y)+(0,-1)=(x,y-1)$$

设 dx = [-1, 0, 1, 0]，dy = [0, 1, 0, -1]，则 (dx[d], dy[d]) 则代表某一方向。其中 dx、dy 分别是偏移量数组，简便起见，称索引 d 为方向。不难看出，在这种定义下，$d=0$ 代表向上，$d=1$ 代表向右，$d=2$ 代表向下，$d=3$ 代表向左。

在这种定义下，坐标的更新公式为

( x ′ , y ′ ) = ( x , y ) + ( d x [ d ] , d y [ d ] ) , d ∈ { 0 , 1 , 2 , 3 } (x',y')=(x,y)+(dx[d],dy[d]),\quad d\in\{0,1,2,3\} (x′,y′)=(x,y)+(dx[d],dy[d]),d∈{0,1,2,3}

在填充的过程中，方向的变化为（初始时向右）

$$1\to 2\to 3\to 0\to 1\to 2\to \cdots$$

由此可得方向的更新公式为 d = (d + 1) % 4。那什么时候更新方向呢？无外乎两种情况：

• 下一个要填充的位置越界（只有在填充最外圈的时候才会遇到）；
• 下一个要填充的位置已经被填充过。

#include <iostream>

using namespace std;

int q[100][100];

int main() {
    int n, m;
    cin >> n >> m;
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
    int x = 0, y = 0, d = 1;  // 初始位于(0, 0)，方向向右

    for (int i = 1; i <= n * m; i++) {
        q[x][y] = i;
        int a = x + dx[d], b = y + dy[d];  // 获取下一个要填充的位置
        if (a < 0 || a >= n || b < 0 || b >= m || q[a][b]) {
            d = (d + 1) % 4;
            a = x + dx[d], b = y + dy[d];  // 矫正下一个要填充的位置
        }
        x = a, y = b;
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++)
            cout << q[i][j] << ' ';
        cout << endl;
    }

    return 0;
}