目录
TSL握手过程
RSA密钥协商握手过程
TLS第一次握手
TLS第二次握手
客户端验证证书
TLS第三次握手
TLS 第四次握手
RSA 算法的缺陷
TSL握手过程
HTTP 由于是明文传输,所谓的明文,就是说客户端与服务端通信的信息都是肉眼可见的,随意使用一个抓包工具都可以截获通信的内容。
所以安全上存在以下三个风险:
-
窃听风险,比如通信链路上可以获取通信内容,用户号容易没。
-
篡改风险,比如强制植入垃圾广告,视觉污染,用户眼容易瞎。
-
冒充风险,比如冒充淘宝网站,用户钱容易没。
HTTPS 在 HTTP 与 TCP 层之间加入了 TLS 协议,来解决上述的风险。
HTTP和HTTPS结构对比:

TLS 协议是如何解决 HTTP 的风险的呢?
-
信息加密:HTTP 交互信息是被加密的,第三方就无法被窃取;
-
校验机制:校验信息传输过程中是否有被第三方篡改过,如果被篡改过,则会有警告提示;
-
身份证书:证明百度页面是真正的百度网站;
TLS的握手过程:

上图简要概述了TLS握手过程,其中每一个框都是一条记录,多条记录可以组合称一个TCP数据包发送,所以通常经过四次消息就可以完成TLS握手过程。HTTPS 是应用层协议,需要先完成 TCP 连接建立,然后完成 TLS 握手过程后,才能建立通信安全的连接。
事实上,不同的密钥交换算法,TLS 的握手过程可能会有一些区别(上图的握手过程是DHE密钥协商的过程,主要区别是DHE/ECDHE协商有server key exchange的握手过程,而RSA没有)。
这里先简单介绍下密钥交换算法,因为考虑到性能的问题,所以双方在加密应用信息时使用的是对称加密密钥,而对称加密密钥是不能被泄漏的,为了保证对称加密密钥的安全性,所以使用非对称加密的方式来保护对称加密密钥的协商,这个工作就是密钥交换算法负责的。
RSA密钥协商握手过程

TLS第一次握手
客户端首先发送一个Client Hello消息,向服务器打招呼,消息里面有客户端使用的TLS版本号、支持的密码套件列表,支持压缩算法,以及生成的随机数(Client Random),这个随机数会被服务端保留,因为它是生成对称加密密钥的材料之一。

TLS第二次握手
在服务器收到客户端的Client Hello消息后,会确认TLS版本号是否支持,和从密码套件列表中选择一个密码套件,还有选择压缩算法(安全性原因,一般不压缩),以及生成随机数(*Server Random*)。然后返回Server Hello消息,该消息包括TLS版本号和随机数,,然后从客户端的密码套件列表中选择一个合适的密码套件。

可以看到,服务端选择的密码套件是 “Cipher Suite: TLS_RSA_WITH_AES_128_GCM_SHA256”。
它是有固定格式和规范的。基本的形式是「密钥交换算法 + 签名算法 + 对称加密算法 + 摘要算法」, 一般 WITH 单词前面有两个单词,第一个单词是约定密钥交换的算法,第二个单词是约定证书的验证算法。比如刚才的密码套件的意思就是:
-
由于 WITH 单词只有一个 RSA,则说明握手时密钥交换算法和签名算法都是使用 RSA;
-
握手后的通信使用 AES 对称算法,密钥长度 128 位,分组模式是 GCM;
-
摘要算法 SHA256 用于消息认证和产生随机数;
就前面这两个客户端和服务端相互打招呼的过程,客户端和服务端就已确认了 TLS 版本和使用的密码套件,而且你可能发现客户端和服务端都会各自生成一个随机数,并且还会把随机数传递给对方,作为后续生成会话密钥的条件。此时服务端为了确认自己的身份,发送一个Server Certificate给客户端,该消息就包含数字证书。

随后,服务端发送Server Hello Done消息,目的为了告诉客户端,我已经把该给你的东西都给你了,本次打招呼完毕。

客户端验证证书
数字证书和CA机构
数字证书通常包含:
-
公钥;
-
持有者信息;
-
证书认证机构(CA)的信息;
-
CA 对这份文件的数字签名及使用的算法;
-
证书有效期;
-
还有一些其他额外信息;
数字证书作用:用来认证公钥持有者的身份,防止第三方冒充。
服务端的证书都是由 CA (Certificate Authority,证书认证机构)签名的,CA 就是网络世界里的公安局、公证中心,具有极高的可信度,所以由它来给各个公钥签名,信任的一方签发的证书,那必然证书也是被信任的。
数字证书签发和验证流程

CA 签发证书的过程,如上图左边部分:
-
首先 CA 会把持有者的公钥、用途、颁发者、有效时间等信息打成一个包,然后对这些信息进行 Hash 计算,得到一个 Hash 值;
-
然后 CA 会使用自己的私钥将该 Hash 值加密,生成 Certificate Signature,也就是 CA 对证书做了签名;
-
最后将 Certificate Signature 添加在文件证书上,形成数字证书;
客户端校验服务端的数字证书的过程,如上图右边部分:
-
首先客户端会使用同样的 Hash 算法获取该证书的 Hash 值 H1;
-
通常浏览器和操作系统中集成了 CA 的公钥信息,浏览器收到证书后可以使用 CA 的公钥解密 Certificate Signature 内容,得到一个 Hash 值 H2 ;
-
最后比较 H1 和 H2,如果值相同,则为可信赖的证书,否则则认为证书不可信。
TLS第三次握手
客户端验证完证书后,认为可信则继续往下走。接着,客户端就会生成一个新的随机数 (pre-master),用服务器的 RSA 公钥加密该随机数,通过「Change Cipher Key Exchange」消息传给服务端。
服务端收到后,用 RSA 私钥解密,得到客户端发来的随机数 (pre-master)。
至此,客户端和服务端双方都共享了三个随机数,分别是 Client Random、Server Random、pre-master。
于是,双方根据已经得到的三个随机数,生成会话密钥(Master Secret),它是对称密钥,用于对后续的 HTTP 请求/响应的数据加解密。
生成完会话密钥后,然后客户端发一个「Change Cipher Spec」,告诉服务端开始使用加密方式发送消息。

然后,客户端再发一个「Encrypted Handshake Message(Finishd)」消息,把之前所有发送的数据做个摘要,再用会话密钥(master secret)加密一下,让服务器做个验证,验证加密通信是否可用和之前握手信息是否有被中途篡改过。

可以发现,「Change Cipher Spec」之前传输的 TLS 握手数据都是明文,之后都是对称密钥加密的密文。
TLS 第四次握手
服务器也是同样的操作,发「Change Cipher Spec」和「Encrypted Handshake Message」消息,如果双方都验证加密和解密没问题,那么握手正式完成。
最后,就用「会话密钥」加解密 HTTP 请求和响应了。
RSA 算法的缺陷
使用 RSA 密钥协商算法的最大问题是不支持前向保密。因为客户端传递随机数(用于生成对称加密密钥的条件之一)给服务端时使用的是公钥加密的,服务端收到后,会用私钥解密得到随机数。所以一旦服务端的私钥泄漏了,过去被第三方截获的所有 TLS 通讯密文都会被破解。
为了解决这一问题,于是就有了 DH 密钥协商算法,这里简单介绍它的工作流程。
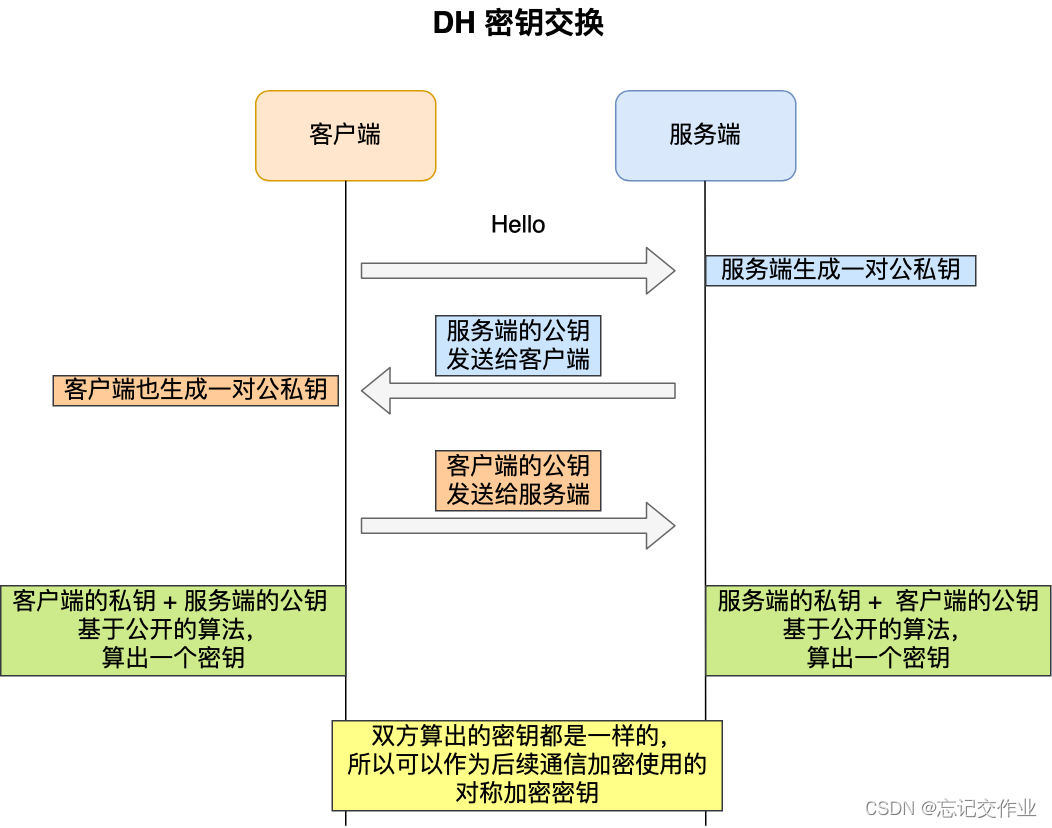
客户端和服务端各自会生成随机数,并以此作为私钥,然后根据公开的 DH 计算公示算出各自的公钥,通过 TLS 握手双方交换各自的公钥,这样双方都有自己的私钥和对方的公钥,然后双方根据各自持有的材料算出一个随机数,这个随机数的值双方都是一样的,这就可以作为后续对称加密时使用的密钥。
DH 密钥交换过程中,即使第三方截获了 TLS 握手阶段传递的公钥,在不知道的私钥的情况下,也是无法计算出密钥的,而且每一次对称加密密钥都是实时生成的,实现前向保密。
但因为 DH 算法的计算效率问题,后面出现了 ECDHE 密钥协商算法,我们现在大多数网站使用的正是 ECDHE 密钥协商算法。