基础知识

并查集常常用来解决图的连通性相关的问题，主要实现了下面几个方法：

class UnionFind {
	private int count; //记录连通分量
    private int[] parent; //节点x的父亲节点是parent[x]
    
    /* 将 p 和 q 连接 */
    public void union(int p, int q);
    /* 判断 p 和 q 是否连通 */
    public boolean connected(int p, int q);
    /* 返回当前节点的根节点 */
    public int find(int x);
    /* 返回图中有多少个连通分量 */
    public int count();
}

其中最重要的是「并」和「查」：

union – 合并两个节点，把两个节点所在的连通分量合并成一个
find – 查找节点所属的连通分量（也就是根）

「集合」使用一个根节点来标识：

数组 parent[] 来表示每个节点的父亲节点，如果自己就是根节点，那么 parent[i] = i，即自己指向自己.

其中方法的具体实现如下：

class UnionFind{
    private int count; //记录连通分量
    private int[] parent; //节点x的父亲节点是parent[x]
    
    public UnionFind(int n){
    	// 一开始互不连通
        this.count = n;
        parent = new int[n];
        // 每个节点是独立的环，父亲节点就是自己
        for(int i = 0;i<n;i++){
            parent[i] = i;
        }
    }
	
	// 将节点p和q连接, 如果两个节点被连通，那么则让其中的一个根节点连接到另一个节点的根节点上
    public void union(int a,int b){
        int parentA = find(a);
        int parentB = find(b);
        if(parentA == parentB) return;
        // 将两颗树合并为一颗
        parent[parentA] = parentB;
        // 连通分量-1
        count--;
    }
	
	// 并查集里寻根的过程，迭代做法，从父节点向上继续找
    public int find1(int x){
          //根节点的parent[x]==x
          while (parent[x]!=x){
              x=parent[x];
          }
          return x;
     }
	
	// 并查集里寻根的过程，递归做法
    public int find2(int u) {
        if (x==parent[x]) return x;
        else return find(parent[u])；
    }
	
	// 判断p和q是否连通:如果两个节点是连通的，那么他们一定拥有相同的根节点
    public boolean connected(int a,int b){
        return find(a) == find(b);
    }
	
	// 返回当前连通分量的个数
    public int getCount(){
        return this.count;
    }
}

优化方法

平衡性优化

思路：当我们每次连接两个节点的时候，不希望出现头重脚轻的情况，而希望到达一种平衡的状态
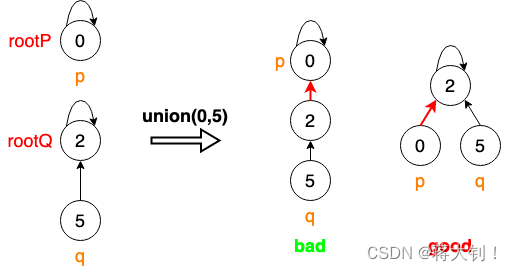
在这里插入图片描述

使用额外的一个数组 size[] 记录每个连通分量中的节点数，每次均把节点数少的分量接到节点数多的分量上，如下图所示：

注意：只有每个连通分量的根节点的 size[] 才可以代表该连通分量中的节点数

private int count;
private int[] parent;
private int[] size;

// 构造函数
public UnionFind (int n) {
    this.count = n;
    parent = new int[n];
    size = new int[n];
    for (int i = 0; i < n; i++) {
        parent[i] = i;
        // 最初，每个连通分量均为 1
        size[i] = 1;
    }
}

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ) return;
    /******** 修改部分 ********/
    if (size[rootP] < size[rootQ]) {
        parent[rootP] = rootQ;
        size[rootQ] += size[rootP]
    } else {
        parent[rootQ] = rootP;
        size[rootP] += size[rootQ]
    }
    /********** end **********/
    count--;
}

路径压缩

分析上述实现的方法，find() 是决定并查集时间复杂度的重要因素。抛开 find() 因素，其他方法的时间复杂度均可视为 $O (1)$ 。所以如果要优化算法的时间复杂度，需要从 find() 入手。

对于有 n 个节点 1 个连通分量的并查集来说，最坏的时间复杂度为 $O (n)$ ，最好的时间复杂度为 $O (1)$

最坏情况：全部只有左子节点
最好情况：n - 1 叉树，即根节点有 n - 1 个子节点

在find()的过程中将树高进行压缩，即子节点尽可能一步指向根节点：

迭代做法，子节点指向父亲节点的父亲节点

public int find(int x) {
    while (parent[x] != x) {
        // 进行路径压缩
        parent[x] = parent[parent[x]];
        x = parent[x];
    }
    return x;

递归做法，由于find()递归返回的是一个根，所以能一次性将这条路径上的节点全部拉平。

private int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

相关题目

参考题目，并查集从入门到出门

684.冗余连接

并查集，原来无向无环的图加入了一条边以后存在了一个环，现在要删除一条边让它继续无环，当有多种删除方案时，选择 edges 中最后出现的边。

聚焦于点，从前向后遍历每一条边，边的两个节点如果不在同一个集合，就将这条边的两个节点加入同一个集合，当遍历到某条边却发现其两个节点已经在同一个集合里，再加入这条边就会成环。

在进行路径压缩以后，find()可以在 $O (1)$ 内找到根节点，因此总体时间复杂度为 $O (N)$ 。

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        UnionFind unionFind=new UnionFind(edges.length);
        for(int[]e:edges){
            if(unionFind.isConnect(e[0],e[1])){
                return e;
            }
            unionFind.union(e[0],e[1]);
        }
        
        return new int[0];
    }

    class UnionFind{
        private int count;
        private int[] parent;
        public UnionFind(int n){
            this.count=n;
            parent=new int[n+1];
            for(int i=1;i<=n;i++){
                parent[i]=i;
            }
        }

        public void union(int a, int b){
            int parentA=find(a);
            int parentB=find(b);
            if(parentA==parentB) return;
            parent[parentA]=parentB;
            this.count--;
        }

        // public int find(int x){
        //     if(parent[x]==x) return parent[x];
        //     else return find(parent[x]);
        // }

        public int find(int x){
            if(parent[x]!=x){
                parent[x]=find(parent[x]);
            }
            return parent[x];
        }

        public boolean isConnect(int a,int b){
            return find(a)==find(b);
        }

        public int getCount(int x){
            return this.count;
        }
    }
}