第三十八章 贪心策略——区间相关问题
- 一、什么贪心策略?
- 二、区间问题合集
- 1、思路:
- 2、问题1: 区间选点
- (1)问题
- (2)思路和证明
- a.思路
- b.证明
- (3)代码
- 3、问题2:
- (1)问题
- (2)思路和证明
- a.思路
- b、证明
- (3)代码
一、什么贪心策略?
贪心策略是一种活在当下,偏短视的策略。每次做的都是对当下最好的选择,然后从局部最优最终推出整体最优。
二、区间问题合集
1、思路:
对于贪心策略中的区间问题往往是利用左右端点去排序,然后猜测一些性质。
2、问题1: 区间选点
(1)问题

(2)思路和证明
a.思路
这道题简单的来说,就是我们选出几个点,这几个点所在的区间能包含所有我们输入的区间,那么在满足这个条件的前提下,我们选出一个最小值,即我们找最少的点。
那么怎么找呢?
我们先把输入的区间映射到数轴上来看这个问题:

如上图所示,我们将所有的区间都映射到数轴上,此时我们尝试着去选点,对于前两个区间而言,我们的A1和A2是我们选的点。很明显,我们选的点越靠右越好。也就是说对于当前的来看,我们选的越靠右越好,这就是当下的最优策略。比如图上的A2点和A1点。
根据这个现象,我们总结出下面的解题思路:
-
1、将区间映射到数轴上(按照右端点从小到大排序)
-
2、按照右端点从小到大枚举区间,看下一个区间的左端点是否小于当前的右端点。
- 如果小于的话,说明当前区间的右端点包含在下一个区间内,也就是说我们选择当前区间的右端点可以包含两个区间。
- 如果大于的话,那么很明显,由于我们的右端点从小到大,所以下一个区间的右端点肯定是当前的右端点,同时下一个区间的左端点也大于我们当前的右端点,这就说明我们当前的右端点不包含在下一个区间内。
-
3、如果是第一种情况,那么我们不用继续在下一个区间内选点,如果是第二种情况,则我们需要选上下一个区间的右端点。
我们先来解决第一个问题,能不能按照左端点来排序?
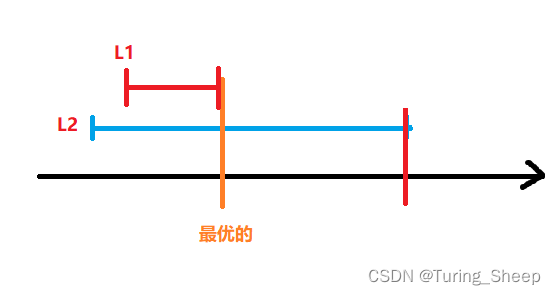
上面的图是按照左端点排序的,如图中的所示,我们的橙色线所对的点是最优的。但是在左端点排序的条件下,我们按照刚才的步骤来看,我们会取出L1和L2的右端点,其实实际上我们只需要选一个。
因此我们只能选择右端点排序。
(其实,如果按照左端点排序,需要从后往前遍历,这种做法也是可以的。)
b.证明
证明:反证法
我们假设存在一个最优解,优于我们的上述贪心算法计算出来的解。
因为这个最优解不符合我们的贪心算法,也就是说,这个最优解中的某些点选的不是最右侧的点。
那么分为以下三种情况:
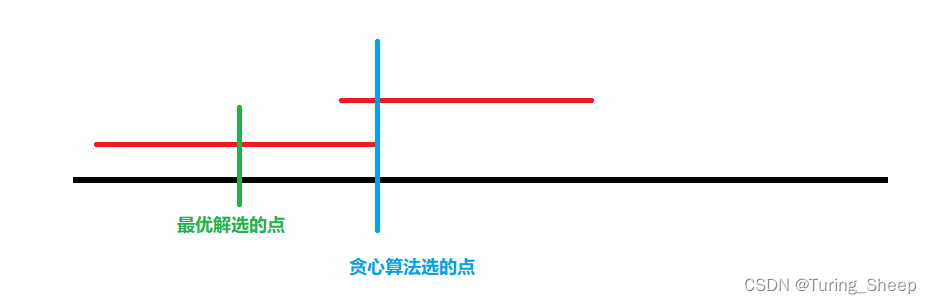
在这种情况下,我们的最优解所选的绿色点是只覆盖了一个区间,因此它需要在下一个区间再选一个点,所以如果只有这一个点和我们的贪心算法得出的结果不一样的话,假设的最优解至少比我们的算法结果多1。
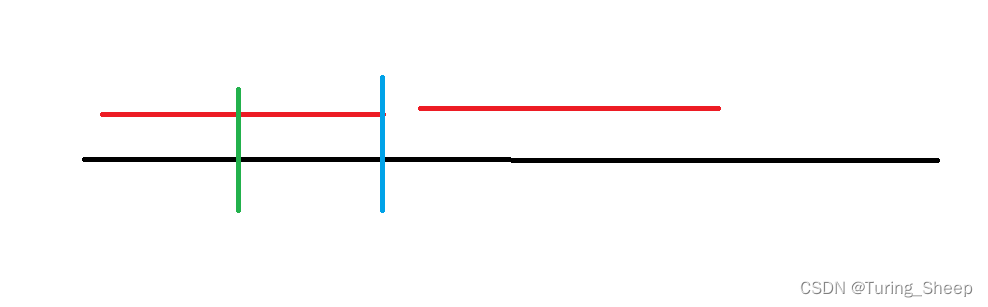
这是第二个情况,但此时我们发现,这两个点是等价的,都没有覆盖下一个点。此时假设的最优解等于我们的算法结果。
第三种情况:

第三种情况就是二者都覆盖了下一个区间,那么二者也是等价的,因此假设的最优解和我们的算法结果也是一样的。
综合上述三种情况,我们假设的最优解大于等于我们的算法结果的,而我们的题目是找一个最小值,也就是说假设的最优解并不是最优的,矛盾,故我们的算法是正确的。
(3)代码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N=1e5+10;
PII a[N];
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int l,r;
scanf("%d%d",&l,&r);
a[i].first=r,a[i].second=l;
}
sort(a,a+n);
int ans=0,ed=-2e9;
for(int i=0;i<n;i++)
{
if(ed<a[i].second)
{
ans++;
ed=a[i].first;
}
}
cout<<ans<<endl;
}
3、问题2:
(1)问题

(2)思路和证明
a.思路
我们还是先将这些区间映射到我们的数轴上。这道题的话,其实和上面那道题的做法是一模一样的。我们把相交的区间看成一个集合。那么我们最终的答案其实就是集合的数量。
我们看下面的这个例子:
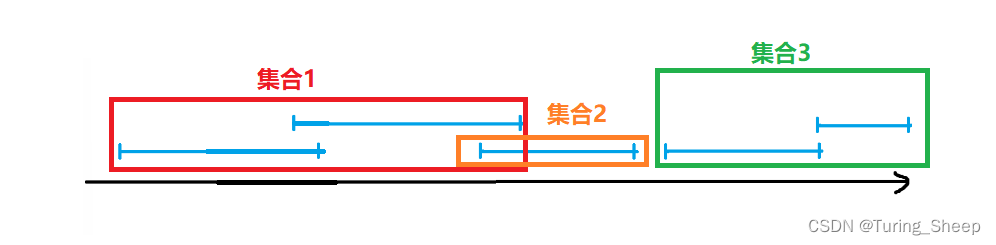
对于每个集合而言,我必定只能选1个区间,这是肯定的。
并且我们尽可能选择一个集合中右端点靠左的那一个,为什么呢?
因为为了能够尽可能多的去选出不相交的区间,我们一定要为后续的区间腾出最大的空间。
所以,如果我们发现一个集合中最靠左的那个区间和某个不在集合内的区间不相交的话,我们就可以将这个不相交的区间分成下一个集合。
那我们如何判断是否相交呢?
我们假设第一个区间就是一个集合,由于这个区间在前面,所以它就是第一个集合内最靠左的。因此,用这个区间的右端点和下一个区间的左端点做比较,如果相交了,那么就属于第一个集合,如果不相交,则结束当前集合,让那个未相交的区间成为一个新的集合。然后继续用新集合内的最靠左的区间的右端点继续去比较。
b、证明
反证法,假设存在一个最优解要比我们的算法算出来的结果还大。
那么由于这个不是我们的算法推出来的,只能说它选的不是集合内靠后的。
但是从图中可知,以集合1为例子,如果我们选了靠右的那个区间,很明显,这个区间覆盖了两个,结果是比我们算出来的结果少1的。
因此,假设不成立。
(3)代码
#include<iostream>
#include<algorithm>
using namespace std;
typedef pair<int,int> pii;
const int N=1e5+10;
int n;
pii a[N];
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
int l,r;
scanf("%d%d",&l,&r);
a[i].first=r,a[i].second=l;
}
sort(a,a+n);
int ans=0,ed=-2e9;
for(int i=0;i<n;i++)
{
if(ed<a[i].second)
{
ans++;
ed=a[i].first;
}
}
cout<<ans<<endl;
return 0;
}