🌈个人主页:聆风吟
🔥系列专栏:算法模板、数据结构
🔖少年有梦不应止于心动,更要付诸行动。
文章目录
- 📋前言
- 一. ⛳️单调栈讲解
- 1.1 🔔单调栈的定义
- 1.2 🔔如何维护一个单调栈
- 1.3 🔔单调栈的用途
- 1.4 🌟模板总结(重点)🌟
- 1.5 🔔单调栈的实例练习
- 二. ⛳️单调队列讲解
- 2.1 🔔单调队列的定义
- 2.2 🔔单调队列的用途
- 2.3 🌟模板总结(重点)🌟
- 2.4 🔔单调栈的实例练习
- 📝结语
📋前言
💬 hello! 各位铁子们大家好哇,今天作者给大家带来了单调栈和单调队列的算法模板讲解,让我们一起加油进步。
📚 系列专栏:本期文章收录在《算法模板》,大家有兴趣可以浏览和关注,后面将会有更多精彩内容!
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
一. ⛳️单调栈讲解
1.1 🔔单调栈的定义
定义:栈内的元素是单调递增或单调递减的栈。
1.2 🔔如何维护一个单调栈
- 单调递增栈:在保持栈内元素单调递增的前提下,如果栈顶元素大于要入栈的元素,将栈顶元素弹出,将新元素入栈。
- 单调递减栈:在保持栈内元素单调递减的前提下,如果栈顶元素小于要入栈的元素,则将栈顶元素弹出,将新元素入栈。
1.3 🔔单调栈的用途

由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己小的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己小的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己大的元素),此时栈顶元素就是数组中左侧第一个比自己小的元素;

由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己大的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己大的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己小的元素),此时栈顶元素就是数组中左侧第一个比自己大的元素;
由此,我们可以看出单调栈的用途是:给定一个序列,指定一个序列中的元素,求解该元素左侧或右侧第一个比自己小或大的元素。
1.4 🌟模板总结(重点)🌟
本文总结的模板是找出每个数左边离它最近的比它大或小的数,右边的可以自行推导(单看模板比较抽象,建议看完下面的题目,在返回来看)
//常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;//栈顶指针
for (int i = 1; i <= n; i ++ )
{
//check函数是判断查找:
//1. 每个数左边第一个比它小的数
//2. 还是每个数左边第一个比它大的数
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}
1.5 🔔单调栈的实例练习
⌈ 在线OJ链接 ⌋
题目:

输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
解题思路:
我们以上面的 3 4 2 7 5 来举例分析,开始遍历 3 这个元素,此时栈为空,那就表明 3 这个元素左侧没有比自身小的元素,将结果 -1 记录一下(或者直接输出)。然后将 3 压入栈中。遍历到 4 时发现 4 大于栈顶的元素 3,表明 4 这个元素左侧第一个比自身小的元素是 3,将结果 3 记录一下(或者直接输出)。遍历到 2 时,发现 2 小于栈顶的元素 4,4 是不可能作为结果输出的,所以需要将栈顶的 4 弹出。弹出之后栈顶的元素就是 3 ,同样 2 仍然小于 3,需要再次将 3 弹出。此时我们发现栈里面已经没有元素了,说明 2 的左侧没有比自身小的元素,将结果 -1 记录一下。然后将 2 压入栈中。其他的元素同理便可以得出,下面给出了动图,这里就不一一讲解了!
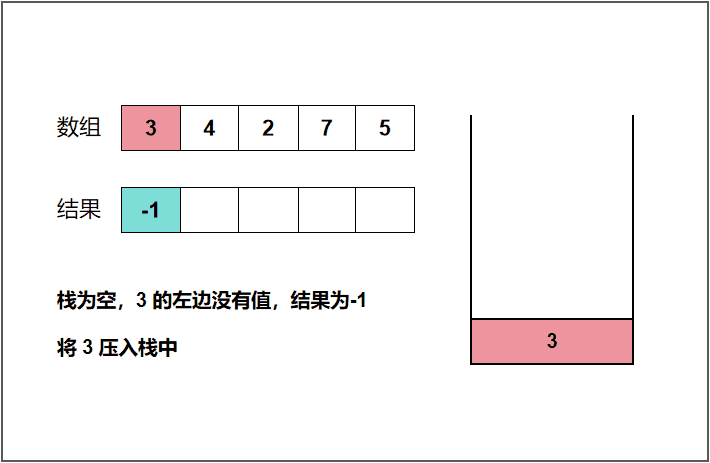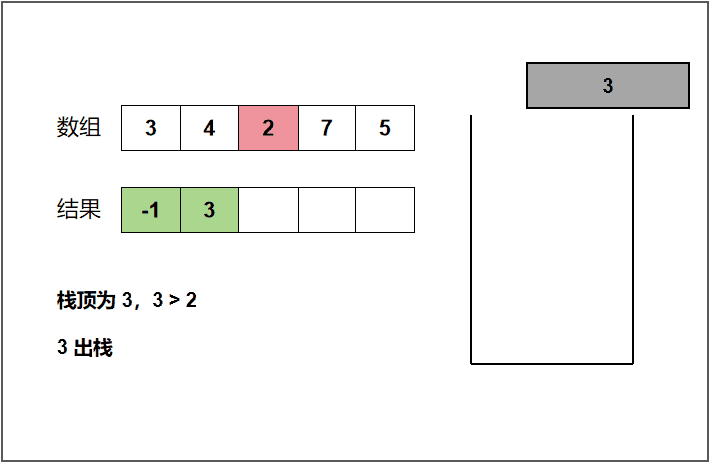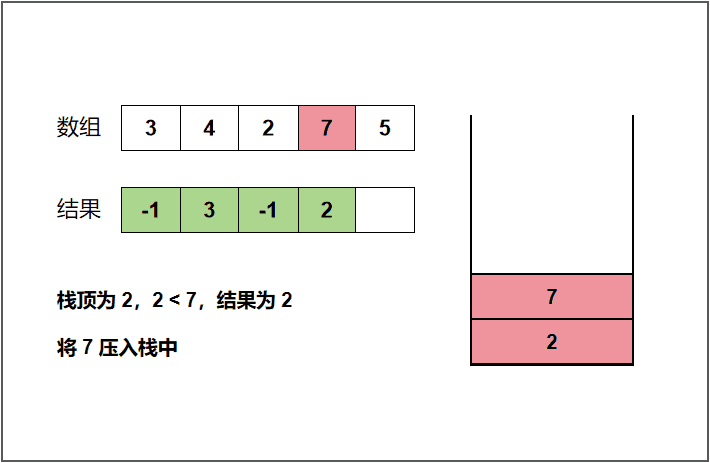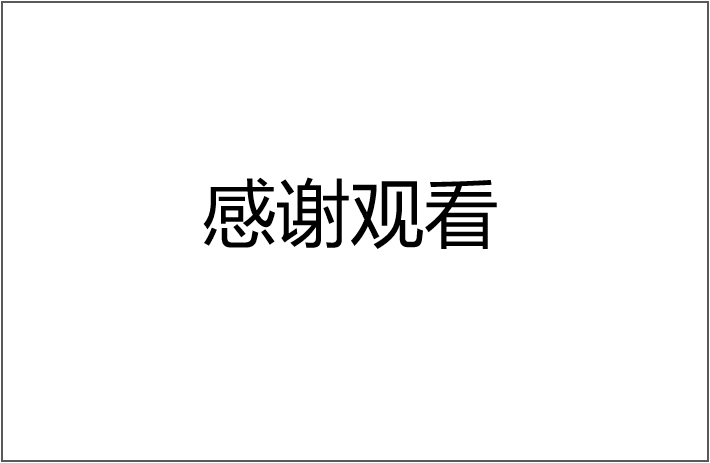
c++代码:
#include <iostream>
using namespace std;
const int N = 100010;
int stk[N], tt;
int main()
{
int n = 0;
cin >> n;
for(int i = 0; i < n; i++)
{
int x = 0;
cin >> x;
//如果栈顶元素大于当前待入栈元素,则出栈
while(tt && stk[tt] >= x) tt--;
if(tt)
{
//栈顶元素就是左侧第一个比它小的元素。
cout << stk[tt] << " ";
}
else
{
//如果栈空,则没有比该元素小的值。
cout << "-1" << " ";
}
//将当前元素加入单调栈中
stk[++tt] = x;
}
return 0;
}
二. ⛳️单调队列讲解
2.1 🔔单调队列的定义
定义:队列内的元素是单调递增或单调递减的队列。
2.2 🔔单调队列的用途
单调队列的用途:在一个滑动窗口中求最值问题
2.3 🌟模板总结(重点)🌟
本文总结的模板主要是找出滑动窗口中的最大值/最小值(单看模板比较抽象,建议看完下面的题目解析,在返回来看)
//常见模型:找出滑动窗口中的最大值/最小值
int hh = 0;//队头
int tt = -1;//队尾
for (int i = 0; i < n; i ++ )
{
// 判断队头是否滑出窗口
while (hh <= tt && check_out(q[hh])) hh ++;
// 判断队尾元素是否出队列
while (hh <= tt && check(q[tt], i)) tt --;
// 将新元素压入队尾
q[ ++ tt] = i;
}
2.4 🔔单调栈的实例练习
⌈ 在线OJ链接 ⌋
题目:


输入样例:
8 3
1 3 -1 -3 5 3 6 7
输出样例:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
解题思路:
在这里我只讲解下求滑动窗口的最小值,最大值的求解可以类比。当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质(此处是单调增),我们需要不断的将新元素与队尾进行比较,如果新元素小于等于队尾元素,那末队尾元素就可以被永久的移除,我们将其弹出队列。不断重复上述过程直到队列为空或者新元素大于队尾元素时,我们将新元素压入队尾中。由于队列中下标对应的元素是严格单调递增的,因此此时的队头下标对应的元素就是滑动窗口的最小值。

c++代码:
#include <iostream>
using namespace std;
const int N = 1000010;
//a[N]存放数组元素
//队列q[N]中存的是原数组的下标
int a[N], q[N];
int hh = 0;//队头
int tt = -1;//队尾
int main()
{
int n, k;
cin >> n >> k;
for(int i = 0; i < n; i++) scanf("%d", &a[i]);
//每个位置滑动窗口中的最小值
for(int i = 0; i < n; i++)
{
if(hh <= tt && i - k + 1 > q[hh]) hh++;//若队首出窗口,hh加1
while(hh <= tt && a[q[tt]] >= a[i]) --tt;//若队尾不单调,tt减1
q[++tt] = i;//下标加到队尾
if(i >= k-1) cout << a[q[hh]] << " ";
}
puts("");
//每个位置滑动窗口中的最大值
hh = 0, tt = -1;
for(int i = 0; i < n; i++)
{
if(hh <= tt && i - k + 1 > q[hh]) hh++;
while(hh <= tt && a[q[tt]] <= a[i]) --tt;
q[++tt] = i;
if(i >= k-1) cout << a[q[hh]] << " ";
}
return 0;
}
📝结语
今天的干货分享到这里就结束啦!如果觉得文章还可以的话,希望能给个三连支持一下,聆风吟的主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就是作者前进的最大动力!