文章目录

• • @[toc]
  • • 问题描述
    • 最小生成树的性质
    • • 证明
    • `Kruskal`算法
    • 时间复杂性
    • `Python`实现

个人主页：丷从心

系列专栏：贪心算法

---

问题描述

• 设$G=(V,E)$是无向连通带权图，$E$中每条边$(v,w)$的权为$c[v][w]$
• 如果$G$的一个子图$G^{{}^{\prime }}$是一棵包含$G$的所有顶点的树，则称$G^{{}^{\prime }}$为$G$的生成树
• 生成树上各边权的总和称为该生成树的耗费，在$G$的所有生成树中，耗费最小的生成树称为$G$的最小生成树

---

最小生成树的性质

• 设$G=(V,E)$是连通带权图，$U$是$V$的真子集，如果$(u,v)\in E$，且$u\in U$，$v\in V-U$，且在所有这样的边中，$(u,v)$的权$c[u][v]$最小，那么一定存在$G$的一棵最小生成树，它以$(u,v)$为其中一条边
• 这个性质有时也称为$MST$性质

证明

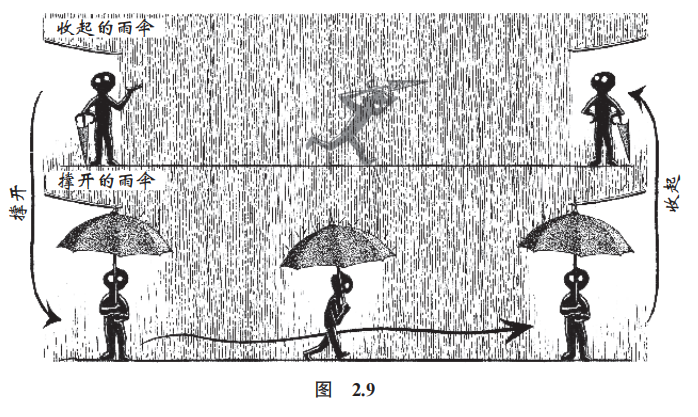
• 假设$G$的任何一棵最小生成树都不包含边$(u,v)$，将边$(u,v)$添加到$G$的一棵最小生成树$T$上，将产生含有边$(u,v)$的圈，并且在这个圈上有一条不同于$(u,v)$的边$(u^{{}^{\prime }},v^{{}^{\prime }})$，使得$u^{{}^{\prime }}\in U$，$v^{{}^{\prime }}\in V-U$，如下图所示

• 将边$(u^{{}^{\prime }},v^{{}^{\prime }})$删去，得到$G$的另一棵生成树$T^{{}^{\prime }}$，由于$c[u][v]\le c[u^{{}^{\prime }}][v^{{}^{\prime }}]$，所以$T^{{}^{\prime }}$的耗费$\le T$的耗费，于是$T^{{}^{\prime }}$是一棵含有边$(u,v)$的最小生成树，与假设矛盾

---

Kruskal算法

• 给定无向连通带权图$G=(V,E)$， V = {   1 , 2 , ⋯   , n   } V = \set{1 , 2 , \cdots , n} V={1,2,⋯,n}
• 首先将$G$的$n$个顶点看成$n$个孤立的连通分支，将所有的边按权从小到大排序，然后从第一条边开始，依边权递增的顺序查看每条边，并按下述方法连接两个不同的连通分支
• 当查看到第$k$条边$(v,w)$时，如果端点$v$和$w$分别是当前两个不同的连通分支$T_1$和$T_2$中的顶点时，就用边$(v,w)$将$T_1$和$T_2$连接成一个连通分支，然后继续查看第$k+1$条边，如果端点$v$和$w$在当前的同一个连通分支中，就直接再查看第$k+1$条边
• 这个过程一直进行到只剩下一个连通分支时为止，此时这个连通分支就是$G$的一棵最小生成树

---

时间复杂性

• 当图的边数为$e$时，Kruskal算法所需的时间是$O(e\log e)$
• 当$e=\Omega (n^2)$是，Kruskal算法比Prim算法差，当$e=o(n^2)$时，Kruskal算法比Prim算法好得多

---

Python实现

class Graph:
    def __init__(self, vertices):
        self.V = vertices  # 图中顶点的数量
        self.graph = []  # 存储图的边的列表

    def addEdge(self, u, v, w):
        self.graph.append([u, v, w])  # 添加边到图的边列表

    def find(self, parent, i):
        if parent[i] == i:  # 如果顶点 i 的根节点是自身, 则返回 i
            return i
        return self.find(parent, parent[i])  # 递归查找 i 的根节点

    def union(self, parent, rank, x, y):
        root_x = self.find(parent, x)  # 查找顶点 x 的根节点
        root_y = self.find(parent, y)  # 查找顶点 y 的根节点

        if rank[root_x] < rank[root_y]:  # 如果 x 的根节点的秩小于 y 的根节点的秩
            parent[root_x] = root_y  # 将 x 的根节点连接到 y 的根节点
        elif rank[root_x] > rank[root_y]:  # 如果 x 的根节点的秩大于 y 的根节点的秩
            parent[root_y] = root_x  # 将 y 的根节点连接到 x 的根节点
        else:  # 如果 x 和 y 的根节点的秩相同
            parent[root_y] = root_x  # 将 y 的根节点连接到 x 的根节点
            rank[root_x] += 1  # 增加 x 的根节点的秩

    def kruskalMST(self):
        result = []  # 存储最小生成树的边的列表
        i = 0  # 当前处理的边的索引
        e = 0  # 已经加入最小生成树的边的数量

        self.graph = sorted(self.graph, key=lambda x: x[2])  # 按照边的权重对图的边进行排序

        parent = []  # 存储顶点的父节点
        rank = []  # 存储顶点的秩
        for node in range(self.V):
            parent.append(node)  # 每个顶点的初始父节点是自身
            rank.append(0)  # 每个顶点的初始秩是 0

        while e < self.V - 1:  # 当最小生成树的边的数量小于 V - 1 时, 继续循环
            u, v, w = self.graph[i]  # 获取当前处理的边的源顶点、目标顶点和权重

            i += 1  # 增加边的索引

            x = self.find(parent, u)  # 查找 u 的根节点
            y = self.find(parent, v)  # 查找 v 的根节点

            if x != y:  # 如果 u 和 v 不在同一个连通分量中(不会形成环路)
                e += 1  # 增加已加入最小生成树的边的数量

                result.append([u, v, w])  # 将该边加入最小生成树的结果中

                self.union(parent, rank, x, y)  # 合并 u 和 v 所在的连通分量

        print('边\t\t权')

        for u, v, weight in result:
            print(f'{u} - {v}\t{weight}')  # 打印最小生成树的边和权重


g = Graph(5)

g.addEdge(0, 1, 2)
g.addEdge(0, 3, 6)
g.addEdge(1, 3, 8)
g.addEdge(1, 2, 3)
g.addEdge(1, 4, 5)
g.addEdge(2, 4, 7)
g.addEdge(3, 4, 9)

g.kruskalMST()

边		权
0 - 1	2
1 - 2	3
1 - 4	5
0 - 3	6

---