博弈论：理解决策背后的复杂动态

1.基本概念

博弈论是一门研究具有冲突和合作元素决策制定的数学理论。它不仅适用于经济学，还广泛应用于政治学、心理学、生物学等领域。博弈论的核心在于分析参与者（称为“玩家”）在特定情境下的策略选择，以及这些选择如何影响最终的结果。

博弈论的两个基本类型是合作博弈和非合作博弈。合作博弈关注的是群体如何通过协作达到共同目标，而非合作博弈则侧重于个体玩家在没有明确协作的情况下的策略选择。

经典的博弈论实例包括“囚徒困境”和“鹰鸽博弈”。这些模型帮助解释了在复杂的社会互动中，个体如何做出可能非最优但相对合理的决策。

博弈案例：

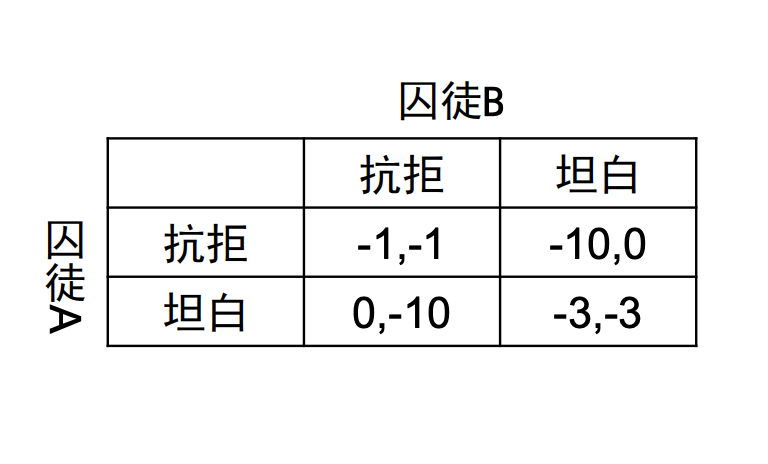
“囚徒困境” 是一个描述两名犯罪嫌疑人被分开审讯时面临选择的经典博弈论例子。如果一个人认罪，而另一个保持沉默，认罪的人会得到较轻的刑罚，而另一个则会受到重刑。如果两人都认罪，他们都会受到中等程度的刑罚。但如果两人都保持沉默，他们都会得到最轻的刑罚。这个例子展示了个体决策之间的复杂互动。

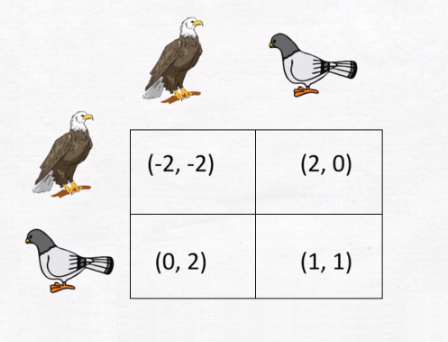
“鹰鸽博弈” 则是一个描述动物在争夺资源时的行为策略的模型。“鹰” 代表攻击性的策略，而"鸽" 代表和平策略。如果两只"鹰"相遇，它们会争斗，造成损害；如果"鹰"遇到"鸽"，"鹰"获得资源，"鸽"则放弃；如果两只"鸽"相遇，它们平和地分享资源。这个模型用于解释动物行为和人类社会中的冲突与合作。

“蛋糕问题”分配蛋糕问题是一个经典的公平分配问题，目标是找到一种方式，让两个人公平地分配一件东西，例如蛋糕。最著名的解决方案是“我切你选”（Cut and Choose）策略，它保证了参与者之间的公平性。

这种方法之所以有效，是因为切割者被激励要尽可能公正地切割蛋糕，因为他知道选择者会选择看起来更大的那一块。如果切割者切得不公平，他最终会得到较小的那一部分。而选择者可以选择他认为更大的那一块，因此，无论切割者如何切，选择者总能确保自己得到至少半块蛋糕。这个过程保证了每个人都有公平的分配机会。

“田忌赛马”（田）忌数与齐诸公子驰逐重射。孙子见其马足不甚相远，马有上、中、下辈。于是孙子谓田忌曰：“君弟重射，臣能令君胜。”田忌信然之，与王及诸公子逐射千
金。及临质，孙子曰：“今以君之下驷与彼上驷，取君上驷与彼中驷，取君中驷与彼下驷。”既驰三辈毕，而田忌一不胜而再胜，卒得王千金。

1.行为主义（Behaviorism）：行为主义是一种心理学理论，主要关注可观察的行为，而不是内在的心理状态。它认为所有的行为都是对外部刺激的反应，可以通过奖励和惩罚等条件反射的形式来学习和改变。行为主义在20世纪上半叶非常流行，对心理学和教育学产生了深远影响。在人工智能领域，行为主义影响了一些早期的AI模型，这些模型专注于通过输入和输出的模式来模拟智能行为，而不是尝试模拟人类大脑的内部工作方式。

2.交互涌现的智能（Emergent Intelligence from Interactions）：这个概念来自于复杂系统理论，主要是指在多个相互作用的部分（如个体、组件或代理）之间的交互中产生的智能行为或性质，这些在单个部分中并不明显。在人工智能领域，这个概念反映在如何通过多个简单的代理或算法的交互来产生复杂、智能的行为。例如，群体智能（如蚁群算法、鸟群算法）就是在许多简单个体的相互作用中涌现出复杂行为的一个例子。

2.纳什均衡

纳什均衡是博弈论中的一个关键概念，由美国数学家约翰·福布斯·纳什在20世纪50年代提出。它指的是一种在非合作博弈中达到的稳定状态，其中每个参与者选择了最佳策略，考虑到其他参与者的选择。

在纳什均衡点，没有任何一个玩家可以通过单方面改变其策略来增加自己的收益。换句话说，每个玩家的策略都是对其他玩家策略的最佳反应。如果所有玩家都达到了这样的状态，那么博弈就达到了均衡。

纳什均衡的主要特点是：

1.互相最佳反应：在纳什均衡中，每个玩家的策略都是对其他玩家已选择策略的最佳反应。

2.稳定性：由于没有玩家能通过改变策略来获得更多的利益，因此没有激励去偏离这个均衡状态。

3.可能的多重均衡：在一些博弈中，可能存在多个纳什均衡点。

纳什均衡在经济学、生物学、社会学、政治学等多个领域都有广泛的应用，它帮助人们理解和预测在竞争和冲突情境中个体或团体的行为。

一句话概括纳什均衡：

纳什均衡是一种情况，在这种情况下，博弈中的每个参与者都选择了最佳策略，考虑到其他人的选择，并且没有人能通过改变自己的选择而获得更多的好处。

剪刀石头布纳什均衡

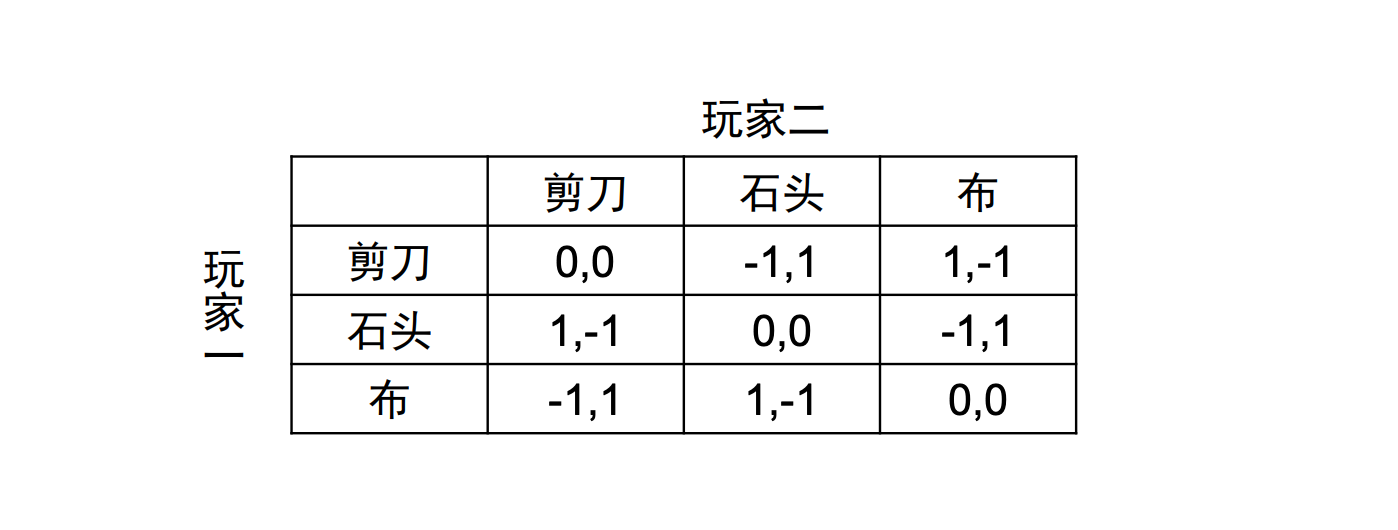
答案：不存在纯策略的纳什均衡

分析剪刀石头布的纳什均衡：

剪刀石头布是一个零和游戏，其中每个玩家有三个选项：剪刀、石头或布。每个选项都能打败另一个选项，被第三个选项打败：石头砸碎剪刀，剪刀剪布，布包石头。在这个游戏中，没有绝对的优势策略，因为任何选择都可能被另一个选项打败。

在剪刀石头布游戏中的纳什均衡发生在每个玩家随机选择三个选项中的任意一个，每个选项被选中的概率都是1/3。这意味着每个玩家的策略都是不可预测的，因此任何玩家都无法通过改变自己的策略来增加获胜的概率。如果一个玩家开始偏好某一种选择，另一个玩家就可以利用这一点来增加自己获胜的机会。因此，唯一的均衡策略是完全随机的选择，这样就没有可利用的模式可以被对手预测和利用。

在实际游戏中，玩家往往不能实现完全的随机化，可能会因为各种心理因素而偏好某一选项。然而，从理论上讲，剪刀石头布的唯一纳什均衡是每个玩家都随机地、且等概率地选择剪刀、石头或布。

3.帕累托最优

帕累托最优（Pareto Optimality）是一个经济学中的概念，由意大利经济学家维尔弗雷多·帕累托命名。它描述的是资源分配的一种状态，在这种状态下，不可能通过改变分配使得至少一个人变得更好而不使任何其他人变得更坏。

换句话说，如果存在一种资源分配方式，在不损害其他任何人的福利的前提下，无法再提高任何一个个体的福利，那么这种分配就是帕累托最优的。在这个状态下，已经达到了效率的最大化，因为任何资源的重新分配都会导致至少一个人的福利减少。

在实际应用中，达到帕累托最优状态是非常困难的，因为它要求在不损害任何个体福利的情况下改进至少一个个体的福利。在多数情况下，政策制定者会寻找某种平衡，以实现最大数量人的福利提升，即便这意味着某些人的福利可能会受到影响。此外，帕累托最优不考虑公平性或福利的分配是否均等，只是单纯地关注是否能在不损害他人的前提下提高至少一个人的福利。

4.社会最优

社会最优（Social Optimality）是一个社会福利的概念，涉及到在整个社会范围内最有效率地分配资源以提高整个社会的福利。这个概念在经济学中是对社会资源配置的理想状态的描述，强调的是社会总福利的最大化。

社会最优的实现通常需要以下几个条件：

1.效率：资源应该被分配到它们最被需要的地方，即生产某种商品和服务的边际成本等于其边际效用。

2.公平：社会最优不仅关心效率，还关心分配的公正性。理想的社会最优状态是每个人的福利都得到了最大化，同时考虑到公平性和平等性。

3.外部性：社会最优考虑到个体行为对社会福利产生的正面或负面外部影响，例如污染。理想状态是所有的外部性都被适当地内化，也就是说，个体在做决策时会考虑他们的行为对他人福利的影响。

在实践中，政府通常通过公共政策来干预，旨在纠正市场失灵，如提供公共品、对负外部性征税（例如碳税）或对正外部性提供补贴，以推动社会资源配置朝向社会最优方向发展。

社会最优与帕累托最优的主要区别在于，社会最优关注的是整个社会的福利，而帕累托最优则是基于个体之间的福利改善而不损害他人的概念。社会最优可能会涉及到重新分配，即使这意味着某些个体的福利相对减少，只要这样的行为能增加社会总福利。

5.GAN中的博弈

生成对抗网络（GANs）是一种通过对抗过程训练的深度学习模型，由两部分组成：生成器（Generator）和判别器（Discriminator）。这两部分在训练过程中相互竞争，从而提高各自的性能。生成器的目标是生成足够真实的数据，以至于判别器无法区分真实数据和生成的数据；而判别器的目标是准确识别出真实的数据和生成器生成的伪造数据。

这个框架内的竞争可以被看作是一个博弈，特别是一个零和博弈，其中一个参与者的收益等于另一个参与者的损失。在这个博弈中，生成器和判别器各自采用策略来最大化自己的收益（或最小化损失）。