在上一篇中我们进行了的并查集相关练习，在这一篇中我们将学习图的知识点。

概念

下面介绍几种在对图操作时常用的算法。

深度优先DFS

深度优先搜索（DFS）是一种用于遍历或搜索树、图等数据结构的基本算法。该算法从给定的起点开始，沿着一条路径直到达到最深的节点，然后再回溯到上一个节点，继续探索下一条路径，直到遍历完所有节点或者找到目标节点为止。

具体步骤如下：

1. 标记起始节点为已访问。

2. 访问当前节点，并获取其所有邻居节点。

3. 遍历所有邻居节点，如果该邻居节点未被访问过，则递归地对该邻居节点进行深度优先搜索。

4. 重复步骤2和步骤3，直到所有能够到达的节点都被访问过。

DFS算法使用了递归或者栈的机制，在每一轮中尽可能深入地探索，并且只有在到达死胡同（无法继续深入）时才会回溯。DFS并不保证先访问距离起始节点近的节点，而是以深度为导向。

DFS算法可以用于寻找路径、生成拓扑排序、解决回溯问题等，但不保证找到最短路径。其时间复杂度为O(V+E)，其中V表示节点数，E表示边数。在树或图的遍历中，DFS通常占用的空间较少，但在最坏情况下可能需要使用大量的栈空间。

简单来说，DFS遵循悬崖勒马回头是岸的原则

拿下图举例：从0一直完左走，走到3，发现没路可走后，回头，继续寻找。

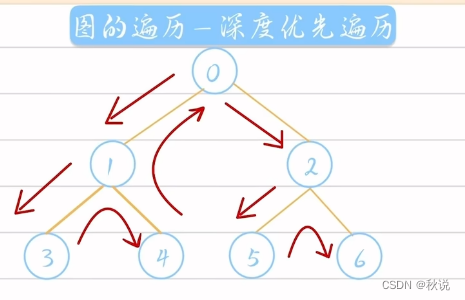
所以：图的深度优先遍历类似于二叉树的先序遍历

伪代码

# 定义图的数据结构
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 定义访问状态数组
visited = {}

# 初始化访问状态
for node in graph:
    visited[node] = False

# 定义DFS函数
def dfs(node):
    # 标记当前节点为已访问
    visited[node] = True
    print(node, end=' ')

    # 遍历当前节点的邻接节点
    for neighbor in graph[node]:
        # 如果邻接节点未被访问，则递归调用DFS函数
        if not visited[neighbor]:
            dfs(neighbor)

# 从起始节点开始进行DFS
start_node = 'A'
dfs(start_node)

广度优先BFS

广度优先搜索（BFS）是一种用于遍历或搜索树、图等数据结构的基本算法。该算法从给定的起点开始，按照距离递增的顺序依次访问其所有邻居节点，并将这些邻居节点加入到一个队列中进行遍历，直到访问到目标节点或者遍历完所有节点。

具体步骤如下：

1. 创建一个队列，将起始节点加入队列中并标记为已访问。

2. 循环执行以下步骤，直到队列为空：

   • 弹出队列头部的节点。
   • 访问当前节点，并获取其所有邻居节点。
   • 遍历所有邻居节点，如果该邻居节点未被访问过，则将其加入队列尾部，并标记为已访问。

3. 循环结束后，所有能够从起始节点到达的节点都已经被访问过了。

BFS算法可以用于寻找最短路径或者解决迷宫等问题，其时间复杂度为O(V+E)，其中V表示节点数，E表示边数。相对于深度优先搜索，BFS搜索更具有层次性，能够保证先访问距离起始节点近的节点，因此在寻找最短路径时更为有效。

如何对一个图进行广度优先遍历呢？

方法是：每一层从左到右进行遍历

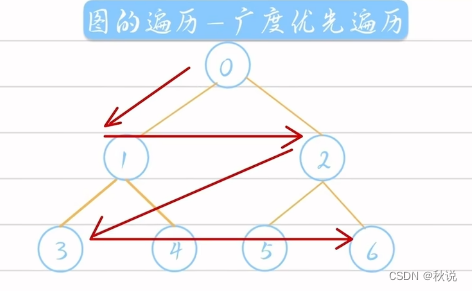
比如下图的结果就是1、2、3、5、6、4、7

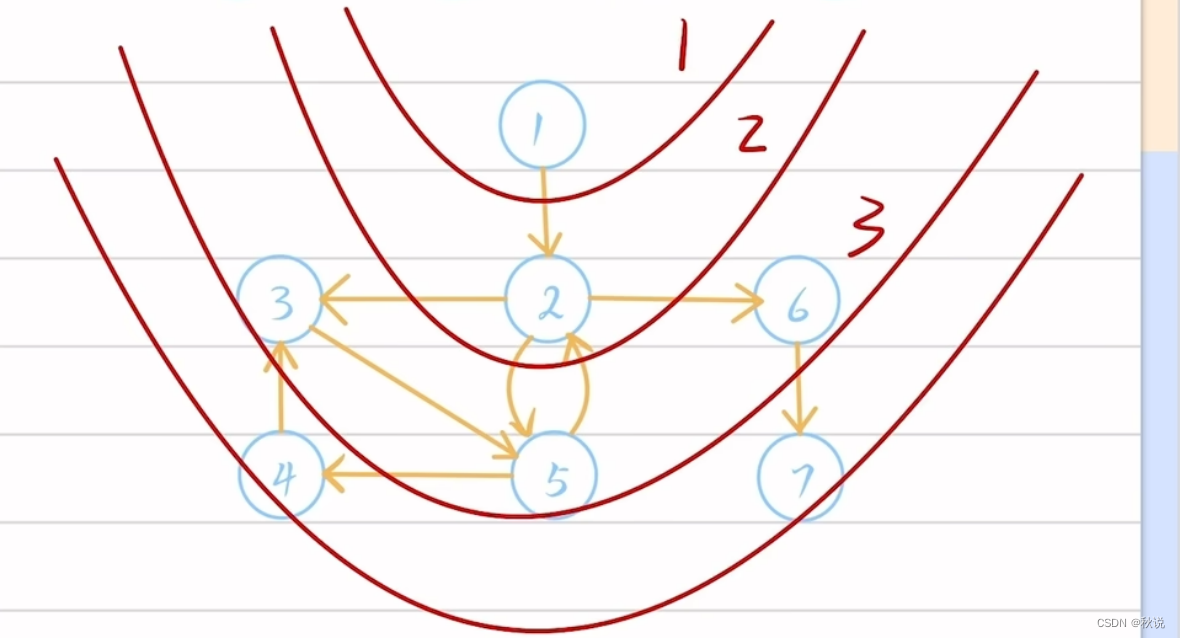
所以图的广度优先遍历类似于树的层次遍历

伪代码

# 定义图的数据结构
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 定义访问状态数组
visited = {}

# 初始化访问状态
for node in graph:
    visited[node] = False

# 定义BFS函数
def bfs(start_node):
    # 创建队列并将起始节点入队
    queue = []
    queue.append(start_node)
    visited[start_node] = True

    while queue:
        # 取出队首节点
        current_node = queue.pop(0)
        print(current_node, end=' ')

        # 遍历当前节点的邻接节点
        for neighbor in graph[current_node]:
            # 如果邻接节点未被访问，则将其入队并标记为已访问
            if not visited[neighbor]:
                queue.append(neighbor)
                visited[neighbor] = True

# 从起始节点开始进行BFS
start_node = 'A'
bfs(start_node)

最短路径算法（Dijkstra）

Dijkstra算法是一种用于解决带权重图中单源最短路径问题的经典算法。它能够找到从起始节点到其他所有节点的最短路径。

该算法的基本思想是通过逐步扩展已知最短路径来逐步确定起始节点到其他节点的最短路径。它维护一个距离字典，记录从起始节点到每个节点的当前最短距离，并使用一个优先队列按照距离的大小进行节点的选择和访问。

具体步骤如下：

1. 创建一个距离字典，并将所有节点的距离初始化为无穷大，将起始节点的距离设置为0。

2. 将起始节点加入优先队列。

3. 循环执行以下步骤，直到优先队列为空：

   • 从优先队列中取出距离最小的节点，作为当前节点。
   • 遍历当前节点的所有邻居节点：
     • 计算从起始节点到当前邻居节点的新距离，即当前节点的距离加上当前节点到邻居节点的边的权重。
     • 如果新距离小于邻居节点的当前距离，则更新邻居节点的距离为新距离，并将邻居节点加入优先队列。

4. 循环结束后，距离字典中记录了从起始节点到所有其他节点的最短距离。

Dijkstra算法适用于有向图或无向图，但要求图中的边权重必须为非负值。它是一种贪心算法，在每一步都选择当前距离最小的节点进行扩展，直到到达目标节点或遍历完所有节点。该算法的时间复杂度为O((|V|+|E|)log|V|)，其中|V|是节点数，|E|是边数。

伪代码

# 定义图的数据结构
graph = {
    'A': {'B': 5, 'C': 3},
    'B': {'A': 5, 'C': 1, 'D': 6},
    'C': {'A': 3, 'B': 1, 'D': 2},
    'D': {'B': 6, 'C': 2}
}

# 定义起始节点和终止节点
start_node = 'A'
end_node = 'D'

# 定义距离字典和前驱节点字典
distances = {}
predecessors = {}

# 初始化距离字典和前驱节点字典
for node in graph:
    distances[node] = float('inf')  # 将所有节点的距离初始化为无穷大
    predecessors[node] = None

# 设置起始节点的距离为0
distances[start_node] = 0

# 定义辅助函数：获取未访问节点中距离最小的节点
def get_min_distance_node(unvisited):
    min_distance = float('inf')
    min_node = None
    for node in unvisited:
        if distances[node] < min_distance:
            min_distance = distances[node]
            min_node = node
    return min_node

# Dijkstra算法主体
unvisited = set(graph.keys())
while unvisited:
    current_node = get_min_distance_node(unvisited)
    unvisited.remove(current_node)

    if current_node == end_node:
        break

    for neighbor, weight in graph[current_node].items():
        distance = distances[current_node] + weight
        if distance < distances[neighbor]:
            distances[neighbor] = distance
            predecessors[neighbor] = current_node

# 重构最短路径
path = []
current_node = end_node
while current_node != start_node:
    path.insert(0, current_node)
    current_node = predecessors[current_node]
path.insert(0, start_node)

# 输出结果
print("最短路径:", path)
print("最短距离:", distances[end_node])

Floyd算法

Floyd算法也称为插点法，是一种用于寻找图中所有节点对之间最短路径的算法，同时也可以用于检测图中是否存在负权回路。

Floyd算法采用动态规划的思想，通过不断更新两个节点之间经过其他节点的最短距离来求解任意两个节点之间的最短路径。具体而言，算法维护一个二维数组 dp，其中 dp[i][j] 表示从节点 i 到节点 j 的最短路径长度。初始化时，若存在一条边从节点 i 到节点 j，则 dp[i][j] 的初值为这条边的边权；否则，dp[i][j] 被赋值为一个足够大的数，表示节点 i 无法到达节点 j。

接下来，我们通过枚举一个中间节点 k，来更新所有节点对之间的最短路径长度。具体而言，如果 dp[i][j] > dp[i][k] + dp[k][j]，则说明从节点 i 到节点 j 经过节点 k 的路径比当前的最短路径还要短，此时可以更新 dp[i][j] 的值为 dp[i][k] + dp[k][j]。

重复执行上述步骤，直到枚举完所有的中间节点 k，即可得到任意两个节点之间的最短路径长度。如果在更新过程中发现某些节点之间存在负权回路，则说明无法求解最短路径。

#define INF 99999
#define V 4

void floydWarshall(int graph[V][V]) {
  int dist[V][V], i, j, k;
  
  // 初始化最短路径矩阵为图中的边权值
  for (i = 0; i < V; i++)
    for (j = 0; j < V; j++)
      dist[i][j] = graph[i][j];
  
  // 动态规划计算最短路径
  for (k = 0; k < V; k++) {
    for (i = 0; i < V; i++) {
      for (j = 0; j < V; j++) {
        // 如果经过顶点k的路径比直接路径更短，则更新最短路径
        if (dist[i][k] + dist[k][j] < dist[i][j])
          dist[i][j] = dist[i][k] + dist[k][j];
      }
    }
  }
  
  // 打印最终的最短路径矩阵
  for (i = 0; i < V; i++) {
    for (j = 0; j < V; j++) {
      // 如果路径为无穷大，则打印INF；否则打印最短路径值
      if (dist[i][j] == INF)
        printf("%7s", "INF");
      else
        printf("%7d", dist[i][j]);
    }
    printf("\n");
  }
}

拓扑排序

拓扑排序和逆拓扑排序都是用于对有向无环图进行排序的算法。

拓扑排序：对于一个有向无环图，拓扑排序可以得到一组节点的线性序列，使得对于任何一个有向边 (u, v)，在序列中节点 u 都排在节点 v 的前面。以下是拓扑排序的伪代码：

# 定义图的数据结构
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 定义入度字典
in_degree = {}

# 初始化入度字典
for node in graph:
    in_degree[node] = 0

for node in graph:
    for neighbor in graph[node]:
        in_degree[neighbor] += 1

# 定义队列并将入度为0的节点加入队列
queue = []
for node in in_degree:
    if in_degree[node] == 0:
        queue.append(node)

# 进行拓扑排序
result = []
while queue:
    current_node = queue.pop(0)
    result.append(current_node)

    for neighbor in graph[current_node]:
        in_degree[neighbor] -= 1
        if in_degree[neighbor] == 0:
            queue.append(neighbor)

# 输出结果
print(result)

逆拓扑排序

逆拓扑排序：与拓扑排序相反，逆拓扑排序可以得到一组节点的线性序列，使得对于任何一个有向边 (u, v)，在序列中节点 v 都排在节点 u 的前面。以下是逆拓扑排序的伪代码：

# 定义图的数据结构
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 定义出度字典
out_degree = {}

# 初始化出度字典
for node in graph:
    out_degree[node] = len(graph[node])

# 定义队列并将出度为0的节点加入队列
queue = []
for node in out_degree:
    if out_degree[node] == 0:
        queue.append(node)

# 进行逆拓扑排序
result = []
while queue:
    current_node = queue.pop(0)
    result.append(current_node)

    for neighbor in graph[current_node]:
        out_degree[neighbor] -= 1
        if out_degree[neighbor] == 0:
            queue.append(neighbor)

# 输出结果
print(result)

至此，图的知识点就介绍完了，在下一篇中我们将进行图的专项练习。