在上一篇中我们进行了树的专项练习，在这一篇中我们将进行散列表知识点的学习。

概念

散列表（Hash Table），也被称为哈希表或散列映射，是一种常用的数据结构之一。它通过将键（key）映射到值（value）来实现高效的数据存储和检索。

散列表的主要思想是利用哈希函数将键转换成对应的索引，然后将值存储在该索引位置上。当需要查找或插入元素时，再次使用哈希函数计算出对应的索引，从而快速定位到目标位置。

散列表的优势在于具有高效的查找和插入操作。由于直接通过索引进行访问，时间复杂度通常为O(1)，即常数时间。

装填因子： 设m和n分别表示表长和表中填入的结点数，则将α=n/m定义为散列表的装填因子(Load Factor)。α越大，表越满，冲突的机会也越大。通常取α≤1。

然而，在极端情况下，散列表的性能可能会下降，例如哈希冲突（多个键映射到同一个索引位置）的发生，这会导致链表的长度增加，进而影响到操作的效率。为了解决这个问题，可以采用一些方法，本文介绍两种方法。

伪代码

// 定义散列表的数据结构
struct HashTable {
    int size; // 散列表的大小
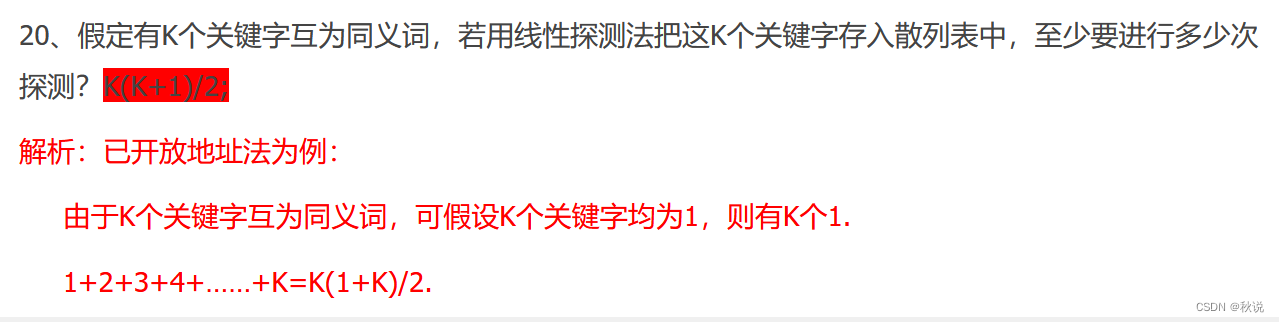
    vector<vector<pair<Key, Value>>> table; // 存储键值对的二维向量数组
};

// 初始化散列表
HashTable Initialize(int size) {
    HashTable hashTable;
    hashTable.size = size;
    hashTable.table.resize(size); // 根据指定的大小调整table的大小
    return hashTable;
}

// 哈希函数，将键映射到散列表的索引位置
int HashFunction(Key key, int size) {
    // 根据键的特性，选择适当的哈希函数来计算散列值
    // 返回散列值对散列表大小取模，得到索引位置
    return hashValue % size;
}

// 向散列表中插入键值对
void Insert(HashTable& hashTable, Key key, Value value) {
    int index = HashFunction(key, hashTable.size); // 计算键的散列值并得到索引位置
    hashTable.table[index].push_back(make_pair(key, value)); // 在索引位置插入键值对
}

// 从散列表中删除指定键的键值对
void Delete(HashTable& hashTable, Key key) {
    int index = HashFunction(key, hashTable.size); // 计算键的散列值并得到索引位置
    vector<pair<Key, Value>>& bucket = hashTable.table[index]; // 获取索引位置的桶
    for (auto it = bucket.begin(); it != bucket.end(); ++it) {
        if (it->first == key) {
            bucket.erase(it); // 删除键值对
            break;
        }
    }
}

// 在散列表中查找指定键的值
Value Search(HashTable& hashTable, Key key) {
    int index = HashFunction(key, hashTable.size); // 计算键的散列值并得到索引位置
    vector<pair<Key, Value>>& bucket = hashTable.table[index]; // 获取索引位置的桶
    for (const auto& entry : bucket) {
        if (entry.first == key) {
            return entry.second; // 返回找到的值
        }
    }
    return defaultValue; // 如果未找到，则返回默认值
}

线性探测法

线性探测法（Linear Probing）是一种解决散列表中哈希冲突的开放寻址法。当哈希函数将键映射到一个已经被占用的位置时，线性探测法会依次往后查找下一个空闲位置，直到找到一个可用的位置为止。

具体来说，当进行插入或查找操作时，如果键在哈希表中的位置已经被占用，线性探测法会通过逐个检查相邻位置的方式，找到下一个可用的位置。如果下一个位置也被占用，则继续往后查找，直到找到一个空闲位置或者遍历整个散列表。

线性探测法的优势在于实现简单，不需要维护额外的数据结构。它可以将冲突的元素存储在散列表中的连续位置，减少了对内存的访问时间，有利于缓存性能的提升。此外，线性探测法还具有较好的空间利用率，因为所有元素都存储在同一个散列表中。

平方探测法

平方探测法（Quadratic Probing）是解决散列表中哈希冲突的一种开放寻址法。与线性探测法不同，平方探测法在查找下一个可用位置时使用了平方的增量来避免元素聚集在一起的问题。

具体来说，当进行插入或查找操作时，如果哈希函数将键映射到一个已经被占用的位置，平方探测法会通过使用平方的增量来寻找下一个可用位置。例如，在第一次冲突时，会尝试移动1^{2=1个位置，如果仍然冲突，则尝试移动2}2=4个位置，依次类推。这样可以有效地避免连续的冲突，减少了元素聚集在一起的情况，提高了性能。

平方探测法的优势在于相对于线性探测法，它能够更均匀地分布元素，减少了聚集性，提高了散列表的性能。此外，平方探测法也无需维护额外的数据结构，实现较为简单。

查找成功的平均查找长度

比如给定
    22  43  15
0   1   2   3   4   5   6   7（表长为7）
求查找成功的平均查找长度？

当查找22时，查找长度为1
查找43时，查找长度为2
15时，为3
所以查找成功的平均查找长度为（1+2+3）/元素个数=6/3=2

查找失败的平均查找长度

比如给定
98  22 30  87   11  40  6   20（冲突）
0   1   2   3   4   5   6   7  8  9  10
求查找失败的平均查找长度？

接着假设给一个元素x
x只能从0映射到6（因为编号7是迫不得已才有位置的）
所以分母是7
当x映射到0时查找失败，则查找9次（查找编号0~7+查找为空）
当x映射到1时查找失败，则查找8次（查找编号1~7+查找为空）
当x映射到2时查找失败，则查找7次（查找编号2~7+查找为空）
...
当x映射到6时查找失败，则查找3次（查找编号6~7+查找为空）
所以分子是（9+8+7+...+3）=42

所以查找失败的平均查找长度为42/7

接下来我们开始散列表的专项练习

判断题

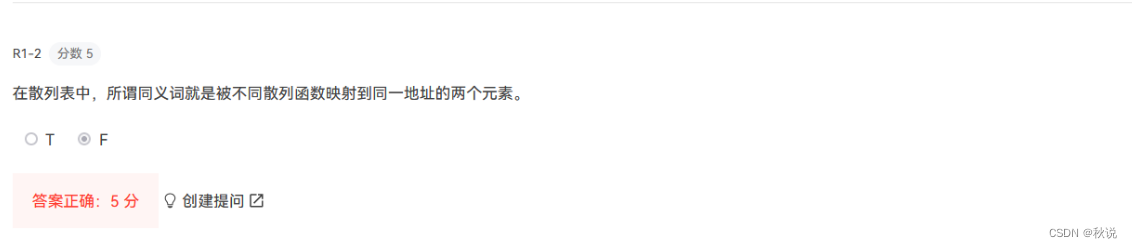
1.平均查找长度与节点个数无关的查找方法是：哈希（散列表）法（对）

2.在散列表中，所谓同义词就是：具有相同散列地址的两个元素（对）

3.将M个元素存入用长度为S的数组表示的散列表，则该表的装填因子为M/S。（对）

4.即使把2个元素散列到有100个单元的表中，仍然有可能发生冲突。（对）

5.

6.

7.

解析：
表格为 0 1 2 3 4 5 6 7 8 9
先插入2，2%11=2，所以插入到编号2的位置
0 1 2 3 4 5 6 7 8 9
2
再插入2，理应插到编号2的位置，但2被占，（2+1^2)%11=3，所以插入到编号为3的位置
0 1 2 3 4 5 6 7 8 9
2 2
再插入2，理应插到编号2的位置，但2被占，（2+1^{2)%11=3，所以插入到编号为3的位置，但3被占，（2+2}2）%11=6，所以插到编号为6的位置
再插入2，理应插到编号2的位置，但2被占，（2+1^{2)%11=3，所以插入到编号为3的位置，但3被占，（2+2}2）%11=6，但6被占，（2+3^2）%11=0，所以插到编号为0的位置

8.
9.

10.
解析：解析：如果是按取模10的话，会产生冲突。

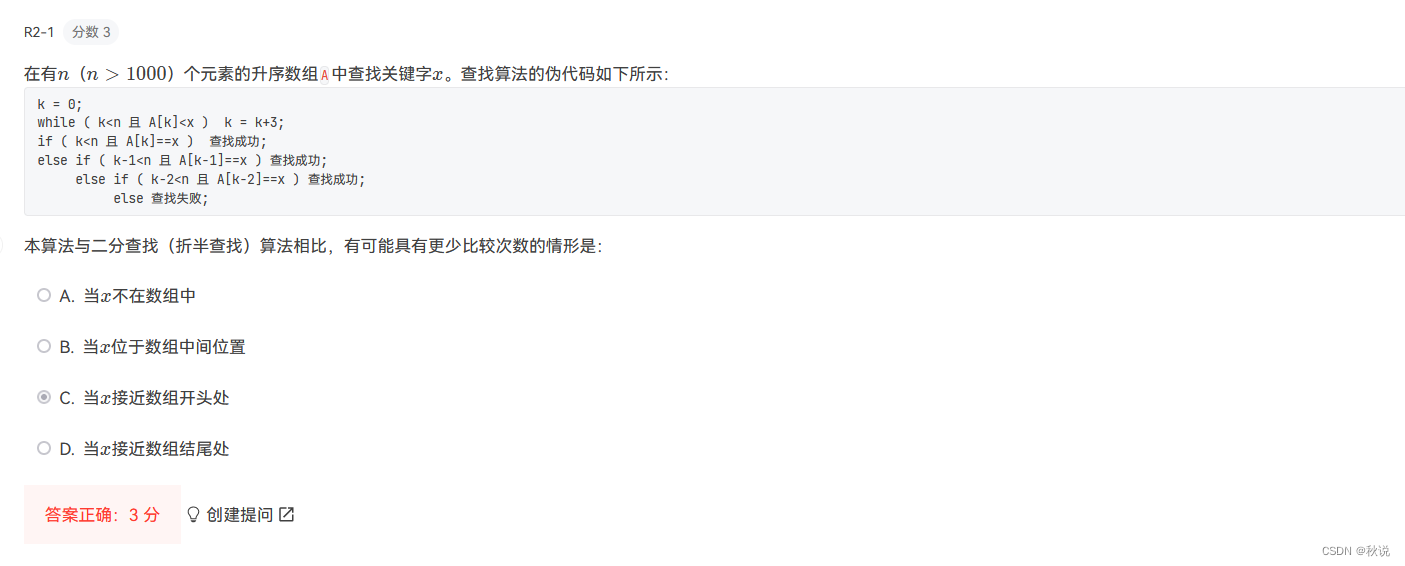
选择题

解析：26%17=9
25%17=8
72%17=4
38%17=4，冲突，所以放在5
8%17=8，冲突，所以放9，但又冲突，所以放10
18%17=1
58%17=8，冲突，放11

2.

3.在第一次发现冲突之前插入的数字个数 除以 表长度 得到 装填因子

4.

5.

6.

6%11=6
25%11=3
39%11=6 冲突 6+1^2=7
61%11=6 冲突 6-1^2=5

7.
解析：

8.

9.
解析：

98  22 30  87   11  40  6   
0   1   2   3   4   5   6   7  8  9  10
插入20时，20本该占编号为6的位置，但被占，所以后移

98  22 30  87   11  40  6   20
0   1   2   3   4   5   6   7  8  9  10


接着假设给一个元素x
x只能从0映射到6（因为编号7是迫不得已才有位置的）
所以分母是7
当x映射到0时查找失败，则查找9次（查找编号0~7+查找的末尾为空）
当x映射到1时查找失败，则查找8次（查找编号1~7+查找的末尾为空）
当x映射到2时查找失败，则查找7次（查找编号2~7+查找的末尾为空）
...
当x映射到6时查找失败，则查找3次（查找编号6~7+查找的末尾为空）
所以分子是（9+8+7+...+3）=42

所以查找失败的平均查找长度为42/7