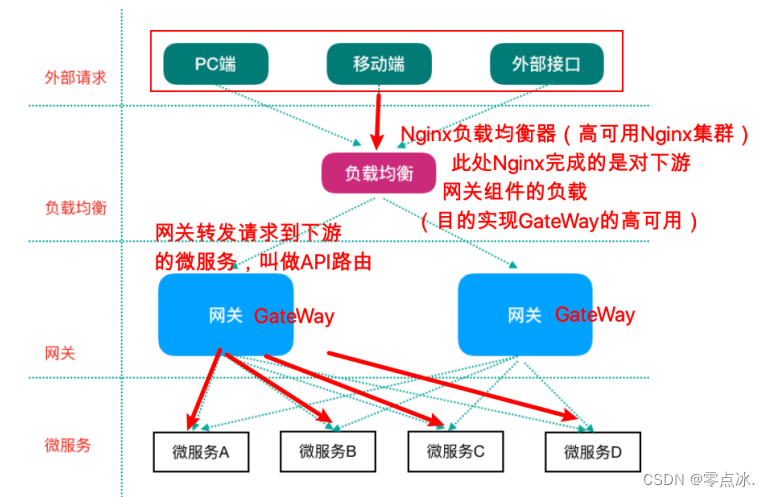
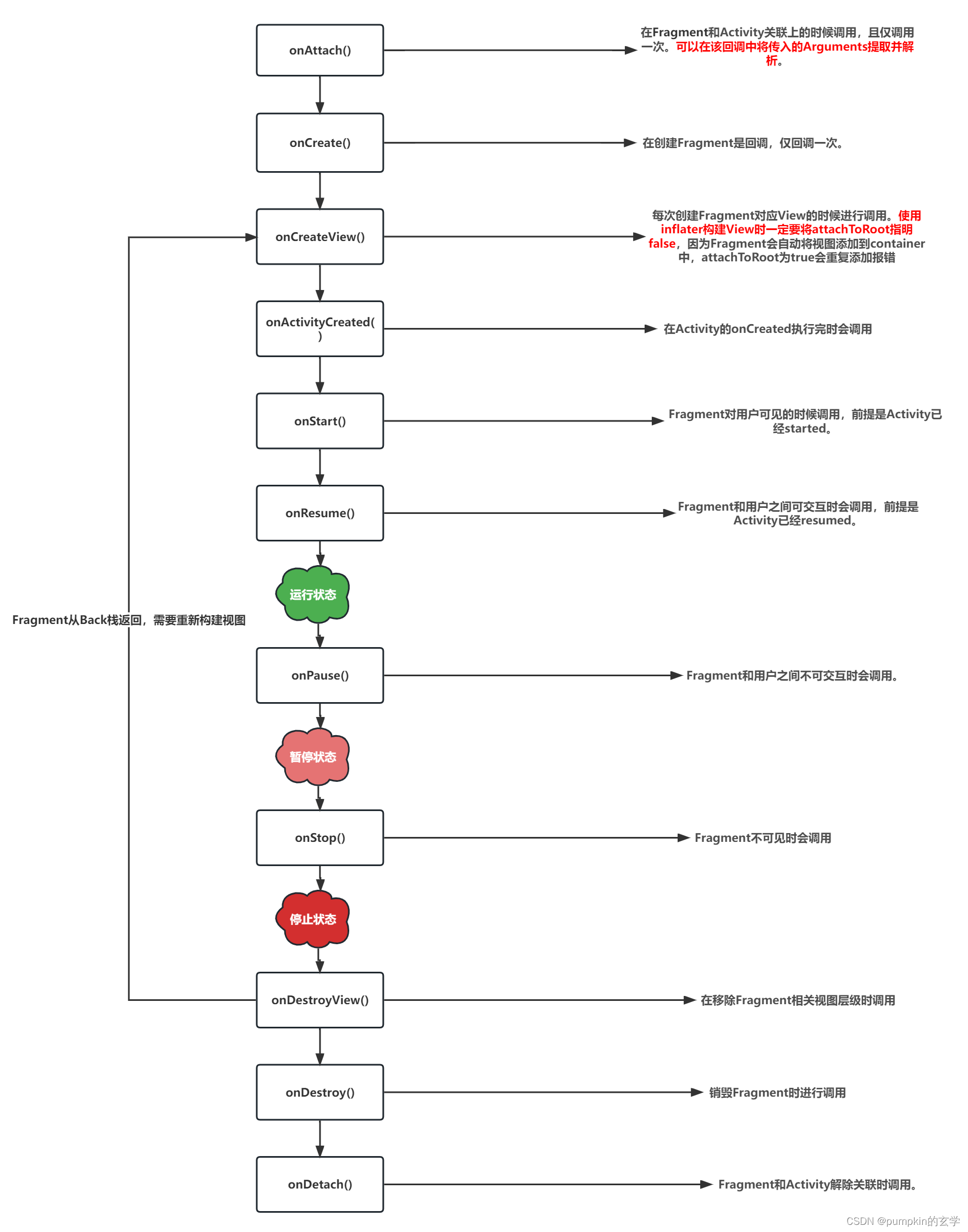
本文ppt来自深蓝学院《机器人中的数值优化》

目录

1 凸集的定义

2 凸集的运算

---

1 凸集的定义

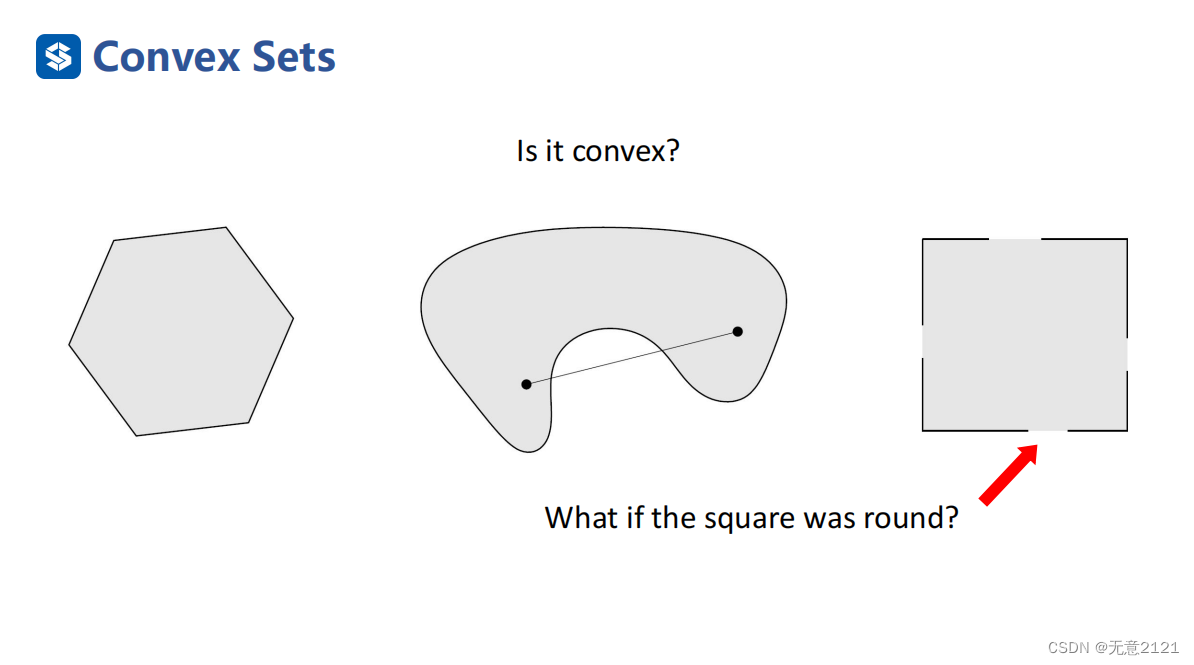
集合中任意两点连线形成的线段属于这个集合，这个集合是凸集。

注意：是否是凸集，集合的边界是否属于这个集合很重要

这涉及到构造最小凸包的问题。

上面列出的超平面、半空间等等都是凸集的典型代表

锥不一定是凸集，比如锥的横截面是非凸集合，那么锥也是非凸的。

上面的二阶锥是通过增加一个维度产生的。

半正定的锥为何是凸集可以利用在集合中取A，B，证明他们的凸组合仍然在这个集合里。

2 凸集的运算

凸集的并集不一定是凸或非凸，凸集的交集一定是凸集。

凸集的sum与product一定是凸集。

 

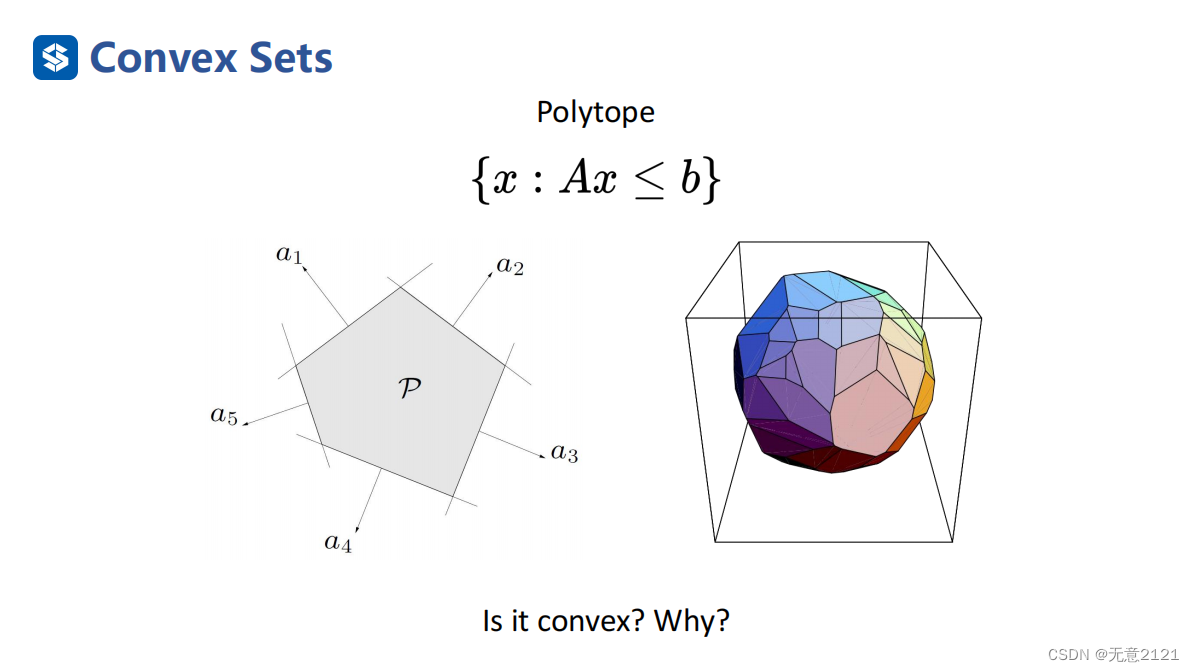
超平面的交集是凸集，以后的障碍物或者是ego-car都常用此来表示。

这是另一种半定锥的定义形式：任何一个向量x代入不等式都成立，而此不等式的本质是一个线性不等式，也就是相当于一个半空间，半空间的交集一定是凸的，但唯一有疑问的一点是无限个凸集的交集还是不是凸的？