【数据结构】五、数组与广义表

news2024/12/28 18:05:57

目录

一、定义

二、计算数组元素地址

三、稀疏矩阵快速转置

稀疏矩阵的表示

稀疏矩阵快速转置

四、广义表

一、定义

我们所熟知的一维、二维数组的元素是原子类型。广义表中的元素除了原子类型还可以是另一个线性表。当然所有的数据元素仍然属于同一类型。

这里的数组可以是顺序结构，也可以是链式结构。

二、计算数组元素地址

公式：

对于二维数组：

行优先：首地址 + [ (行标 - 行起始编号) * 列总数 + (列标 - 列起始编号) ] * 每个元素占的空间

列优先：首地址 + [ (列标 - 列起始编号) * 行总数 + (行标 - 行起始编号) ] * 每个元素占的空间

行和列标号别标反了

例一：

一个二维数组A，行下标的范围是1到6，列下标的范围是0到7，每个数组元素用相邻的6个字节存储，存储器按字节编址。那么，这个数组的体积是（ ）个字节

答案：288       (6-1+1)*(7-0+1)*6

例二：

设数组a[1…60, 1…70]的基地址为2048，每个元素占2个存储单元，若以列序为主序顺序存储，则元素a[32,58]的存储地址为（ ）

答案：8950     2048+[(58-1)*60+(32-1)]*2

 例三：

假设以行序为主序存储二维数组A=array[1..100,1..100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]=（ ）

答案：818

例四：

数组A[0..5,0..6]的每个元素占五个字节,将其按列优先次序存储在起始地址为1000的内存单元中,则元素A[5,5]的地址是(  )

答案：1175

例五：

假设有三维数组A(7×9×8)，每个元素用相邻的6个字节存储，存储器按字节编址。已知A的起始存储位置（基地址）为1000，末尾元素A[6][8][7]的第一个字节地址为多少？

答案：4018    1000+(7×9×8-1)×6

三、稀疏矩阵快速转置

稀疏矩阵：大部分为0，非零元素较少的矩阵

稀疏矩阵的表示

1.线性表

会浪费很多空间

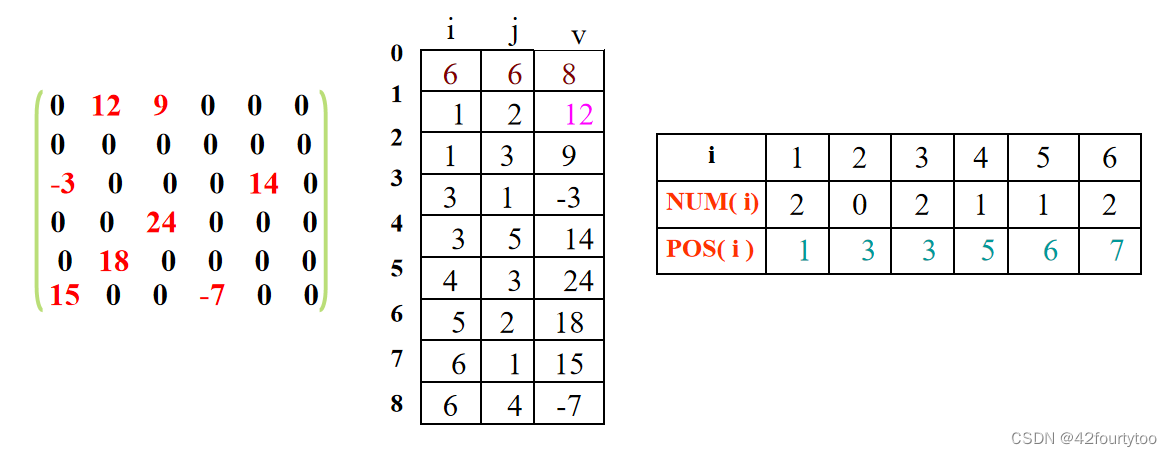
2.三元组表示法

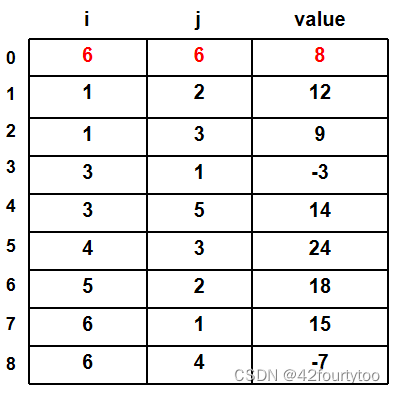
第零行记录总行数，总列数和总非零元素个数；其他行按行优先记录非零元素的位置和值 

为了高效访问稀疏矩阵中任一非零元素，引入辅助向量：

num(i)：记录每行非0元素个数

pos(i)： 记录稀疏矩阵中每行第一个非0元素在三元组中的序号

pos计算公式：

pos(1)＝1

pos(i)＝pos(i-1)+num(i-1)

稀疏矩阵快速转置

目的：已知原矩阵的三元组，求转置后矩阵的三元组。而且原三元组仅遍历一遍，也就是说将原三元组每条信息直接送入新三元组对应位置

所以我们需要一个指示迁移位置的数组cpos

由于转置使得每一列的第一个非零数成为每一行的第一个非零数，而三元组又是以行优先排列的，所以cpos反映了原矩阵每一列首非零元在新三元组中的编号

相当于按列遍历了原矩阵，把转置矩阵每一行的首非零元先写入新三元组对应位置

cpos计算方法：cpos第一位默认为1，也就是原矩阵第一列首非零元要放在新三元组第一行。cpos后一位等于cpos前一位加前一列非零元个数（num数组负责记录每列的非零元素个数）

遍历旧三元组，cpos[列数] = 新三元组中的行号。迁移一个元素后，把对应的cpos加一

由于旧矩阵从上往下从左往右遍历，所以每一列第一个拿到的元素肯定是首非零元，说明本方法合理

代码（有误）：

/*快速转置的目的是通过一次遍历旧三元组，就能把原非零数的信息放到新三元组对应位置上

所以我们需要一个指示迁移位置的数组cpos

由于转置使得每一列的第一个非零数成为每一行的第一个非零数，而三元组又是以行优先排列的，所以cpos反映了每一列首非零元在新三元组中的编号

相当于按列遍历了原矩阵，把转置矩阵每一行的首非零元安排好了

计算方法：cpos第一位默认为1，也就是原矩阵第一列首非零元要放在新三元组第一行。cpos后一位等于cpos前一位加前一列非零元个数

然后遍历旧三元组时，根据列数进行索引，由于旧矩阵从上往下从左往右遍历，所以每一列第一个拿到的元素肯定是首非零元

迁移一个元素后，把对应的cpos加一*/
#include<stdio.h>
#include<stdlib.h>

#define MAXTRIPLE 25    //三元组非零元素最大个数

typedef int elemtype;

typedef struct triple {
	int row;
	int col;
	elemtype e;
}triple;      //三元组节点，包括非零元素的行号，列号，值

typedef struct {
	triple data[MAXTRIPLE + 1];
	int mrow, mcol, mnum;     //列表的总行数，总列数，非零个数，描述的是三元组。data第一行描述稀疏矩阵的行数、列数、非零数
}tsmatrix;   //三元组列表

void creatematrix(elemtype* mat, int row, int col)  //创建矩阵
{
	printf("输入元素：");
	for (int i = 0; i < row; i++)
		for (int j = 0; j < col; j++)
			scanf_s("%d", &mat[(i - 1) * col + j]);
}

void printmatrix(elemtype* mat, int row, int col) {
	for (int i = 0; i < row; i++) {
		for (int j = 0; j < col; j++)
			printf("%d ", mat[(i - 1) * col + j]);
		printf("\n");
	}
	printf("\n");
}

void inittriple(tsmatrix* tri, elemtype* mat, int row, int col) {   //生成三元组

	tri->mcol = 3;
	tri->mrow = 0;
	tri->mnum = 0;
	for (int i = 0; i < row; i++) {
		for (int j = 0; j < col; j++)
			if (mat[(i - 1) * col + j] != 0) {
				tri->mnum++;   //新增节点，列表非零元素和行数都增加
				tri->mrow++;
				tri->data[tri->mnum].e = mat[(i - 1) * col + j];
				tri->data[tri->mnum].row = i;
				tri->data[tri->mnum].col = j;
			}

	}
	tri->data[0].row = row;
	tri->data[0].col = col;
	tri->data[0].e = tri->mnum;    //三元组第一行放稀疏矩阵的信息
}

void printtriple(tsmatrix* tri){  //打印三元组

	printf("三元组矩阵为:\n");
	printf("行\t列\t值\n");
	int i;
	for (i = 0; i <= tri->mrow; i++) {
		printf("%d\t%d\t%d\n", tri->data[i].row, tri->data[i].col, tri->data[i].e);
	}
}

void tri2mat(tsmatrix* tri) {    //将三元组还原为矩阵

	int i, j;
	elemtype* originmat = (elemtype*)malloc(sizeof(elemtype) * tri->data[0].col * tri->data[0].row);
	if (!originmat) return;

	for (i = 0; i < tri->data[0].row; i++)
		for (j = 0; j < tri->data[0].col; j++)
			originmat[i * tri->data[0].row + j] = 0;  //矩阵先全为0

	for (i = 1; i <= tri->mnum; i++)   //遍历三元组非零元素的信息
		originmat[(tri->data[i].row * tri->data[0].row) + tri->data[i].col] = tri->data[i].e;

	printf("矩阵为：\n");
	for (i = 0; i < tri->data[0].row; i++) {
		for (j = 0; j < tri->data[0].col; j++)
			printf("%d ", originmat[i * tri->data[0].row + j]);
		printf("\n");
	}
}

void fasttrans(tsmatrix* tri) {     //快速转置

	tsmatrix* trans = (tsmatrix*)malloc(sizeof(tsmatrix));  //trans为新的三元组
	if (!trans) return;

	trans->mcol = tri->mcol;     
	trans->mrow = tri->mrow;
	trans->mnum = tri->mnum;
	trans->data[0].col = tri->data[0].row;
	trans->data[0].row = tri->data[0].col;
	trans->data[0].e = tri->data[0].e;     //新旧三元组关于自身的信息（行，列，非零数）相同；矩阵的行列互换，非零数相同

	if (tri->mnum > 0) {

		int i;
		int* num = (int*)malloc(sizeof(int) * tri->data[0].col);  //num数组用来记录矩阵每一列非零个数
		if (!num) return;

		for (i = 0; i < tri->data[0].col; i++)
			num[i] = 0;
		for (i = 1; i <= tri->mnum; i++)
			num[tri->data[i].col]++;

		int* cpos = (int*)malloc(sizeof(int) * tri->data[0].col);  //cpos用来记录计算稀疏矩阵中每列第一个非0元素在新三元组表中存放的位置
		if (!cpos) return;

		cpos[0] = 1;   //cpos首元素默认为1
		for (i = 1; i < tri->data[0].col; i++)
			cpos[i] = cpos[i - 1] + num[i - 1];   //cpos剩下元素计算方法：新cpos=旧cpos+旧num 如：第一列首非零元设为1，第二列首非零元为1跳过第一列非零元个数

		printf("nums:");
		for (i = 0; i < tri->data[0].col; i++)
			printf("%d ", num[i]);
		printf("\n");
		printf("cpos:");
		for (i = 0; i < tri->data[0].col; i++)
			printf("%d ", cpos[i]);
		printf("\n");

		for (i = 1; i <= tri->mnum; i++) {   //三元组数据迁移
			trans->data[cpos[tri->data[i].col]].row = tri->data[i].col;    //以旧三元组中列数为索引，到cpos中去查找它要去的位置，行列交换
			trans->data[cpos[tri->data[i].col]].col = tri->data[i].row;
			trans->data[cpos[tri->data[i].col]].e = tri->data[i].e;   
			cpos[tri->data[i].col]++;      //cpos中数据用过一次后要加一
		}

		printtriple(trans);
		printf("转置后的");
		tri2mat(trans);
	}
	else
		tri2mat(tri);

}

int main() {
	
	int row, col;
	printf("输入稀疏矩阵行数：");
	scanf_s("%d", &row);
	printf("输入稀疏矩阵列数：");
	scanf_s("%d", &col);
	elemtype* mat = (elemtype*)malloc(sizeof(elemtype) * row * col);

	creatematrix(mat, row, col);
	printf("原矩阵为：\n");
	printmatrix (mat, row, col);

	tsmatrix* triple = (tsmatrix*)malloc(sizeof(tsmatrix));
	inittriple(triple, mat, row, col);
	printtriple(triple);

	tri2mat(triple);

	fasttrans(triple);
}

四、广义表

定义：广义表是线性表的推广。广义表中元素既可以是原子类型，也可以是列表

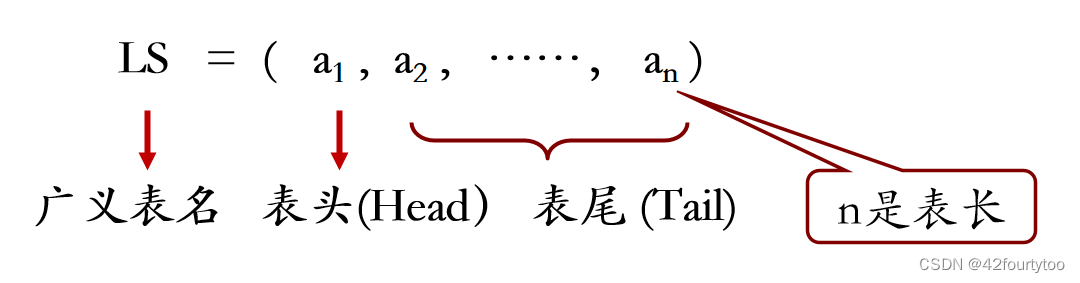
特点：

1.第一个元素是表头，其余元素组成的表称为表尾

2.任何一个非空表，表头可能是原子，也可能是列表；但表尾一定是列表

3.广义表的长度 = 表中元素个数；广义表的深度 = 表中括号的最大重数

4.用小写字母表示原子类型，用大写字母表示列表。

L=( ( ) , (e) , ( a , (b , c , d) ) )，长度为3，深度为3

A=( a , (b , A) )，长度为2，深度为无穷

广义表操作

取表头：表头为单个元素，直接写出表的首位元素即可

取表尾：表尾为列表，写出除了首个元素以外的元素，外面加层括号

练习：

GetTail：(b, k, p, h)                             =(k,p,h)

GetHead：( (a,b), (c,d) )                     =(a,b)

GetTail：( (a,b), (c,d) )                        =((c,d))

GetTail：( GetHead：((a,b),(c,d)) )    =(b)

GetTail: (e)       = ( )

GetHead: ( ( ) )＝( )

GetTail: ( ( ) )   ＝( )

广义表A=(a,b,(c,d),(e,(f,g))),则Head(Tail(Head(Tail(Tail()))))值为(   )
答案：d

已知广义表A=((a,(b,c)),(a,(b,c),d)),则运算head(tail(head()))的结果是(   )

答案：(b,c)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1327726.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Docker容器的日常维护和故障排除

Docker容器的日常维护和故障排除

Docker容器已经成为了现代应用程序开发和部署的核心工具之一。然而&#xff0c;为了确保容器环境的稳定性和可靠性&#xff0c;日常维护和故障排除是必不可少的任务。本文将介绍一些关键的Docker容器维护和故障排除技巧&#xff0c;并提供丰富的示例代码&#xff0c;以帮助大家…
阅读更多...
Flink 状态管理与容错机制(CheckPoint SavePoint)的关系

Flink 状态管理与容错机制(CheckPoint SavePoint)的关系

一、什么是状态 无状态计算的例子&#xff1a; 例如一个加法算子&#xff0c;第一次输入235那么以后我多次数据23的时候得到的结果都是5。得出的结论就是&#xff0c;相同的输入都会得到相同的结果&#xff0c;与次数无关。 有状态计算的例子&#xff1a; 访问量的统计&#x…
阅读更多...
python超实用插件REST Client、autoDocstring、Better Comments

python超实用插件REST Client、autoDocstring、Better Comments

1. autoDocstring 1.1 features 快速生成可以通过制表符浏览的文档字符串片段。在几种不同类型的文档字符串格式之间进行选择。通过pep484类型提示、默认值和变量名称推断参数类型。支持args、kwargs、装饰器、错误和参数类型。 1.2 用法 光标必须位于定义正下方的行上&am…
阅读更多...
【数据结构】四、串

【数据结构】四、串

目录 一、定义 二、表示与实现 定长顺序存储 堆分配存储 链式存储 三、BF算法 四、KMP算法 1.求next数组 方法一 方法二&#xff08;考试方法&#xff09; 2.KMP算法实现 方法一 方法二 3.nextval 4.时间复杂度 本节最重要的就是KMP算法&#xff0c;其他要求不高…
阅读更多...
pip 常用指令 pip config 命令用法介绍

pip 常用指令 pip config 命令用法介绍

&#x1f4d1;pip 常用命令归类整理 pip config 是一个用于管理本地和全局配置的命令行工具。它允许用户获取和设置所有的 pip 配置值。 命令 pip config 有以下参数 list&#xff1a;列出所有的 pip 配置值。edit&#xff1a;编辑 pip 配置文件。get&#xff1a;获取一个配…
阅读更多...
时间是如何定义的

时间是如何定义的

每年365天&#xff0c;每天24小时&#xff0c;每小时60分钟&#xff0c;每分钟60s&#xff0c;这是我们习以为常的时间计量单位&#xff0c;那么在继续往下&#xff0c;1s是多少&#xff1f;几时几刻、几点几分是如何确定的&#xff1f;带着这些问题&#xff0c;展开本文。 1、…
阅读更多...
如何在 openKylin 上使用 ONLYOFFICE 桌面编辑器

如何在 openKylin 上使用 ONLYOFFICE 桌面编辑器

文章作者&#xff1a;ajun ONLYOFFICE 桌面编辑器是一款基于依据 AGPL v.3 许可进行分发的开源办公套件。使用这款应用&#xff0c;您无需保持网络连接状态即可处理存储在计算机上的文档。 本文章基于中国根操作系统 openKylin 操作系统&#xff0c;使用软件商店快速安装与手…
阅读更多...
rtsp视频在使用unity三维融合播放后的修正

rtsp视频在使用unity三维融合播放后的修正

1 rtsp 接入 我们使用unity UE 等三维渲染引擎中使用c编写插件来接入rtsp 视频。同时做融合的时候&#xff0c;和背景的三维颜色要一致&#xff0c;这就要使用视频融合修正技术。包括亮度&#xff0c;对比度&#xff0c;饱和度的修正。在单纯颜色上的修正可以简单使用rgb->…
阅读更多...
Android 权限申请

Android 权限申请

在Android中&#xff0c;从Android 6.0&#xff08;API级别23&#xff09;开始&#xff0c;应用在运行时需要动态申请权限。以下是一些步骤来动态申请权限&#xff1a; 在应用的清单文件&#xff08;AndroidManifest.xml&#xff09;中声明需要的权限。例如&#xff0c;如果应…
阅读更多...
前端FLV视频直播解决方案

前端FLV视频直播解决方案

项目背景&#xff1a; 1. 后台给出一个地址&#xff0c;持续不断的推送flv视频流。 2.前端需要接收视频流&#xff0c;并寻找合适的播放插件。 一开始&#xff1a; 其实用的是xgplayer&#xff08;西瓜视频&#xff09;。 官网地址&#xff1a;西瓜播放器 使用的是直播&a…
阅读更多...
ardupilot开发 --- 风机不停机巡检 篇

ardupilot开发 --- 风机不停机巡检 篇

在哪里创建的siyi实例&#xff1f; 如何传递飞控的时间戳给siyi相机&#xff1f; AP_RTC_ENABLED在waf编译时配置为1&#xff1f;&#xff1f; 如何配置&#xff1f; 在lua脚本中如何获取这个时间AP::rtc().get_utc_usec(utc_usec)&#xff1f;&#xff1f;&#xff1f; inclu…
阅读更多...
【软件问题】解决 SecoClient 提示：接收返回码超时！

【软件问题】解决 SecoClient 提示：接收返回码超时！

解决 SecoClient 提示&#xff1a;接收返回码超时&#xff01; 1.问题描述2.问题查找3.问题解决 系统&#xff1a;Win10 1.问题描述 这段时间因为不小心得了流感&#xff0c;所以需要请病假&#xff0c;而有些工作还得做不能落下&#xff0c;所以得居家办公&#xff0c;因为我…
阅读更多...
【深入解析spring cloud gateway】12 gateway参数调优与分析

【深入解析spring cloud gateway】12 gateway参数调优与分析

本节主要对网关主要的一些参数做一些解释说明&#xff0c;并用压测工具测试一下网关的接口&#xff0c;通过压测来验证参数配置是否合理 一、连接池参数 参数示例 spring:application:name: gatewaycloud:gateway:# http连接设置httpclient:# 全局的响应超时时间&#xff0c…
阅读更多...
大语言模型（LLM）与 Jupyter 连接起来了！

大语言模型（LLM）与 Jupyter 连接起来了！

现在&#xff0c;大语言模型&#xff08;LLM&#xff09;与 Jupyter 连接起来了&#xff01; 这主要归功于一个名叫 Jupyter AI 的项目&#xff0c;它是官方支持的 Project Jupyter 子项目。目前该项目已经完全开源&#xff0c;其连接的模型主要来自 AI21、Anthropic、AWS、Co…
阅读更多...
【Git】在 IDEA 中合并多个 commit 为一个

【Git】在 IDEA 中合并多个 commit 为一个

文章目录 1 未提交到远程分支1.1 需求说明1.2 reset 操作1.3 再次 push 2 已经提交到远程分支2.1 需求说明2.2 rebase 操作2.3 强制 push 分两种情况&#xff1a; 一种是本地提交还没推到远程&#xff0c;这种好处理另一种是已经提交到远程分支&#xff0c;这个略麻烦 1 未提…
阅读更多...
【Java代码审计】RCE篇

【Java代码审计】RCE篇

【Java代码审计】RCE篇 1.Java中的RCE2.ProcessBuilder命令执行漏洞3.Runtime exec命令执行漏洞4.脚本引擎代码注入5.RCE的防御 1.Java中的RCE 在PHP开发语言中有system()、exec()、shell_exec()、eval()、passthru()等函数可以执行系统命令。在Java开发语言中可以执行系统命令…
阅读更多...
如何从 Android 手机免费恢复已删除的通话记录/历史记录？

如何从 Android 手机免费恢复已删除的通话记录/历史记录？

有一个有合作意向的人给我打电话&#xff0c;但我没有接听。更糟糕的是&#xff0c;我错误地将其删除&#xff0c;认为这是一个骚扰电话。那么有没有办法从 Android 手机恢复已删除的通话记录呢&#xff1f;” 塞缪尔问道。如何在 Android 上恢复已删除的通话记录&#xff1f;如…
阅读更多...
STM32CubeMX驱动ST7789

STM32CubeMX驱动ST7789

环境 1、单片机:STM32F103C8T6 2、开发平台&#xff1a;STM32CUBEMXkeil mdk 3、屏幕&#xff1a;ST7789&#xff0c;分辨率240*240 STM32配置 1、使用硬件SPI1驱动屏幕。配置如下&#xff1a; 2、屏幕控制引脚配置&#xff1a; 注意&#xff1a;只配置了DC,RST,CS这3个控…
阅读更多...
BearPi Std 板从入门到放弃 - 后天篇（3）(ESP8266透传点灯)

BearPi Std 板从入门到放弃 - 后天篇（3）(ESP8266透传点灯)

简介 电脑搭建一个TCP Server&#xff0c; ESP8266 串口设置好透传模式, 再由TCP Server发送指令控制灯的亮灭; 开灯指令&#xff1a; led_on回车 &#xff1b; 关灯指令: led_off回车 主芯片: STM32L431RCT6 LED : PC13 \ 推挽输出即可 \ 高电平点亮 串口: Usart1 / LPUART E…
阅读更多...
html之如何设置音频和视频

html之如何设置音频和视频

文章目录 前言一、音频标签&#xff1a;audio1.audio简介2.常用属性controlsautoplayloop代码演示&#xff1a; 二、视频标签&#xff1a;video1.video2.常用的视频元素controlsautoplayloop代码演示&#xff1a; 总结视频元素总结音频元素总结 前言 html中插入音频和视频的方…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023