【AcWing每日一题】4261. 孤独的照片

news2024/11/14 2:31:57

Farmer John 最近购入了 N 头新的奶牛，每头奶牛的品种是更赛牛（Guernsey）或荷斯坦牛（Holstein）之一。

奶牛目前排成一排，Farmer John 想要为每个连续不少于三头奶牛的序列拍摄一张照片。

然而，他不想拍摄这样的照片，其中只有一头牛的品种是更赛牛，或者只有一头牛的品种是荷斯坦牛——他认为这头奇特的牛会感到孤立和不自然。

在为每个连续不少于三头奶牛的序列拍摄了一张照片后，他把所有「孤独的」照片，即其中只有一头更赛牛或荷斯坦奶牛的照片，都扔掉了。

给定奶牛的排列方式，请帮助 Farmer John 求出他会扔掉多少张孤独的照片。

如果两张照片以不同位置的奶牛开始或结束，则认为它们是不同的。

输入格式
输入的第一行包含 N。

输入的第二行包含一个长为 N 的字符串。如果队伍中的第 i 头奶牛是更赛牛，则字符串的第 i 个字符为 G。否则，第 i 头奶牛是荷斯坦牛，该字符为 H。

输出格式
输出 Farmer John 会扔掉的孤独的照片数量。

数据范围
3≤N≤5×10⁵
输入样例：

5
GHGHG

输出样例：

样例解释
这个例子中的每一个长为 3 的子串均恰好包含一头更赛牛或荷斯坦牛——所以这些子串表示孤独的照片，并会被 Farmer John 扔掉。

所有更长的子串（GHGH、HGHG 和 GHGHG）都可以被接受。

自己的思路：

输入字符串之后记录两种牛的种类的数量
对于每一个子字符串，查看这个字符串剩下的牛的数量是否符合
如果某一种牛的数量为1，那么这一组照片应该被扔掉

#include<iostream>
using namespace std;

const int N = 5e5+10;
int n, h = 0, g = 0, res = 0, sum = 1;
char str[N];
int main(){	
	cin >> n;
	scanf("%s", str);
	for(int i = 0; i < n; i++){		
		if(str[i] == 'H') h++;
		if(str[i] == 'G') g++;
	} 
	int sumh = h, sumg = g;
	for(int i = 0; i < n; i++){
		int sg = sumg, sh = sumh; 
		for(int j = n-1; j >= i+2; j--){
			if(sg == 1 || sh == 1)		//如果其中有一种牛的数量是1 
				res++;					//扔掉的孤独的照片数量加一 
			if(sg == 0 || sh == 0)		//如果某一种牛的数量为0 
				break;					//没有能使得照片扔掉的序列，剪枝 
			//如果没有牛的数量是1
			if(str[j] == 'G') sg--;		//把后面这种牛的数量减掉，指针前移 
			if(str[j] == 'H') sh--;
			
		}
		if(str[i] == 'G') sumg--;		//把前面这种牛的数量减掉，指针后移 
		if(str[i] == 'H') sumh--;
	}	
	cout << res;	
	return 0;
}

问题很显然，这样会在任何情况下的时间复杂度都是O(n²)
这样在内层的for循环加入剪枝

if(sg == 0 || sh == 0)		//如果某一种牛的数量为0 
	break;					//没有能使得照片扔掉的序列，剪枝

会在部分较好情况下把时间复杂度降一点，最好的时间复杂度为O(n)
但是在较坏的情况下，还是有很高的复杂度
还有个问题就是res的数量级用int是存不下的，需要long long

//测试复杂度的代码：
	cin >> n;
//	scanf("%s", str);
	for(int i = 0; i < n; i++){	
		if(i%2 == 0) str[i] = 'G';
		else str[i] = 'H';
//		str[i] = 'H';	
		if(str[i] == 'H') h++;
		if(str[i] == 'G') g++;
	}

y总的方法：

因为要扔掉的图片中有一个字母只出现一次，所以我们可以去枚举只出现一次的图片是哪一个
我们要找的是，只包含一个G或H的、长度大于等于三的字串的数量
符合要求的字符串只能包含一个G或H，所以其他位置是另外一个字母
枚举每一个位置，会出现三种情况

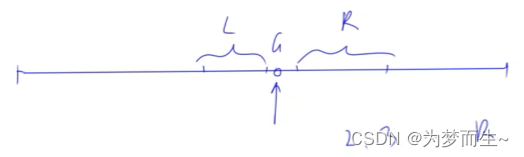
对于每一个位置的字母，在字串的长度大于等于三的情况下

左边和右边至少存在一个不同于当前位置的字母。设左边有L个，右边有R个，那么左边和右边分别可以取1,2,…,L个，1,2,…,R个（这种情况至少一边取一个）。那么这种情况符合乘法原理，一共是L*R种情况。
左边没有不同于当前位置字母的字母。那这种情况只能从右边取。同样设右边有R个（不同于当前位置字母的字母），那么可以取2,3,…,R个，有R-1种情况
右边没有不同于当前位置字母的字母。那这种情况只能从左边取。同样设左边有L个（不同于当前位置字母的字母），那么可以取2,3,…,L个，有L-1种情况

最后把这三种情况加起来就是答案，并且这种方法的时间复杂度为O(n)

举个例子：

假设枚举到某一个位置时，当前位置的字母为G，那么想要得到符合条件的结果，只能从其他地方取H

对于上面的第一种情况，左边可以取1,2,…,L个H，右边可以取1,2,…,R个H，符合乘法原理
对于第二种情况，只能从右边取H但是至少取两个
对于第三种情况，之能从左边取，最少两个

附上代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 500010;

int n;
char str[N];
int l[N], r[N];		//表示左边和右边有多少个与当前位置不一样的连续的字母

int main()
{
    scanf("%d", &n);
    scanf("%s", str);
	//先处理左边
    for (int i = 0, h = 0, g = 0; i < n; i ++ )
        if (str[i] == 'G') l[i] = h, h = 0, g ++ ;	//当前位置存的G，记录左边扫过的连续的H的数量，连续h的数量就被清空了，开始加g的数量
        else l[i] = g, g = 0, h ++ ;				//当前位置存的H，记录左边扫过的连续的G的数量，连续g的数量就被清空了，开始加h的数量
	//再处理右边
    for (int i = n - 1, h = 0, g = 0; i >= 0; i -- )
        if (str[i] == 'G') r[i] = h, h = 0, g ++ ;
        else r[i] = g, g = 0, h ++ ;
	//所有的情况加起来
    LL res = 0;
    for (int i = 0; i < n; i ++ )
        res += (LL)l[i] * r[i] + max(l[i] - 1, 0) + max(r[i] - 1, 0);

    printf("%lld\n", res);
    return 0;
}
//
//作者：yxc
//链接：https://www.acwing.com/activity/content/code/content/5012677/
//来源：AcWing
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。