递归指的是在函数的定义中使用函数自身的方法。
举个例子:
从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?"从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?'从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?……'"
递归是一种计算方法,它的每一步计算都可以被分解为更小规模的相同的计算,因此一个问题可以通过不断重复的分解来解决。一个典型的例子是计算阶乘N!的递归方法:
递归和数学中的数学归纳法思想类似,数学归纳法是用小一些的问题f(N-1)来证明大一些的问题f(N)成立,而递归则是通过小一些的问题f(N-1)来求大一些的问题f(N)的解。一个可以用递归解决的问题一定是一个数学归纳问题,即一个命题如果对f(N-1)成立,那么对f(N)也成立,只有这样才能用相同的计算来表示所有的计算过程。
递归算法需要两个步骤:分解问题和合并问题的解。分解问题是将大问题分解为小问题,这种分解是可重复的,以阶乘的递归算法为例,它的原始问题f(N)可以被分解为f(N-1)*N,用同样的方式,f(N-1)可以被分解为f(N-2)*(N-1),以此类推,直到问题被分解到最小的问题f(1) ,最小问题的解一定是已知的,在这里 f(1) = 1;合并问题的解是按照与分解问题相反的顺序,将小问题的解合并为大问题的解,还是以阶乘的递归算法为例,当我们得到f(1),就可以得到f(2) = 2*f(1),以此类推,由f(N-1)的解,我们可以得出f(N)的解f(N) = f(N-1)*N。
语法格式如下:
void recursion()
{
statements;
... ... ...
recursion(); /* 函数调用自身 */
... ... ...
}
int main()
{
recursion();
}流程图:
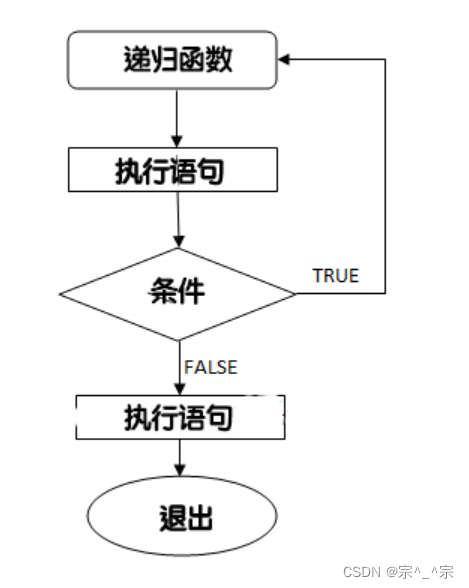
C 语言支持递归,即一个函数可以调用其自身。但在使用递归时,程序员需要注意定义一个从函数退出的条件,否则会进入死循环。
递归函数在解决许多数学问题上起了至关重要的作用,比如计算一个数的阶乘、生成斐波那契数列,等等。
数的阶乘
下面的实例使用递归函数计算一个给定的数的阶乘:
#include <stdio.h>
double factorial(unsigned int i)
{
if(i <= 1)
{
return 1;
}
return i * factorial(i - 1);
}
int main()
{
int i = 15;
printf("%d 的阶乘为 %f\n", i, factorial(i));
return 0;
}当上面的代码被编译和执行时,它会产生下列结果:
15 的阶乘为 1307674368000.000000斐波那契数列
下面的实例使用递归函数生成一个给定的数的斐波那契数列:
#include <stdio.h>
int fibonaci(int i)
{
if(i == 0)
{
return 0;
}
if(i == 1)
{
return 1;
}
return fibonaci(i-1) + fibonaci(i-2);
}
int main()
{
int i;
for (i = 0; i < 10; i++)
{
printf("%d\t\n", fibonaci(i));
}
return 0;
}当上面的代码被编译和执行时,它会产生下列结果:
0
1
1
2
3
5
8
13
21
34