一、说明
今天的帖子主要是关于使用折线回归找到最佳值。即将某条曲线分解成包络线段,然后用分段回归方式优化。但它也涉及使用 SAS 和 R 的剂量反应研究和样条曲线。这不是第一篇关于这些主题的文章,但我确实想在其中添加折线。只是因为它还在使用。
二、药物剂量的应用
寻找最佳值并不是什么新鲜事。为了找到最佳值,您通常会进行剂量反应研究。剂量反应研究旨在找出物质的数量或接触量之间的关系(剂量)及其对动物的总体影响(反应)。要有效地设计剂量反应研究,您需要了解生物系统并提出一个有针对性的问题:
- 有剂量效应的生物学证据吗?
- 最佳剂量是多少?
- 需要什么剂量才能产生不同于对照/零反应的反应?
- 剂量关系的本质是什么?
不同的变量可以通过不同的方式建立不同的关系。下面是示例(最大值、最小值、山脊和鞍点)。这些内容之前已在此处进行了展示和解释。
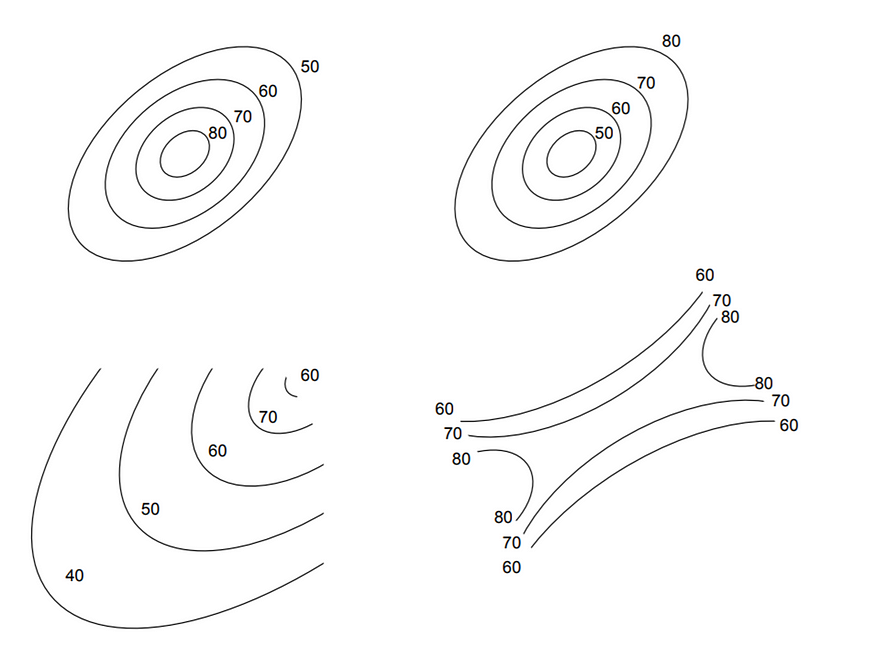
剂量反应关系(顺时针):最大、最小、鞍形和脊形。
剂量反应最好以 3D 而不是 2D 方式探索,并且最好使用不同的视角来显示。正如您所看到的,两个或三个变量是可行的,但想象一下必须以图形方式表示 6 因素交互作用。如果没有某种形式的聚类,几乎不可能做到这一点。
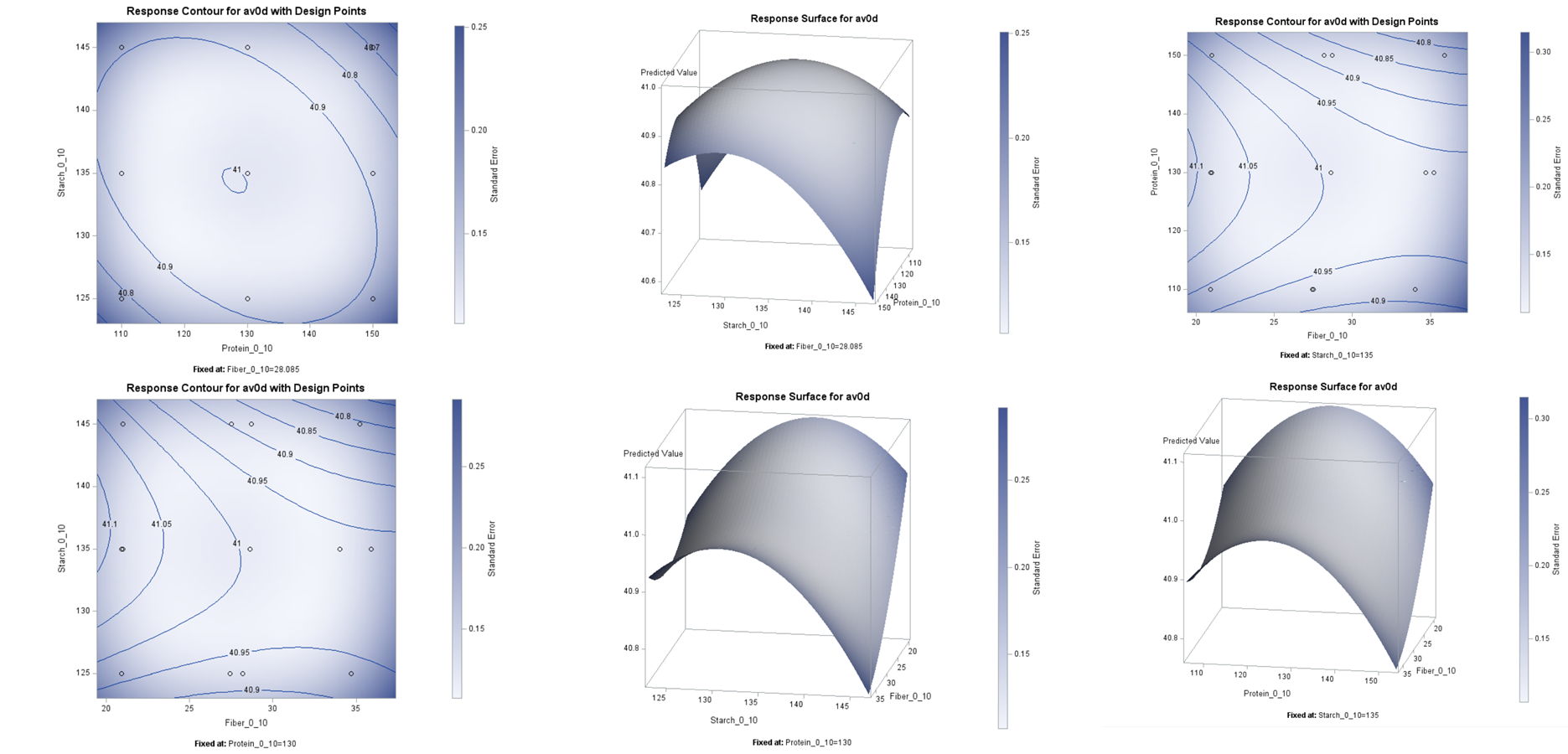
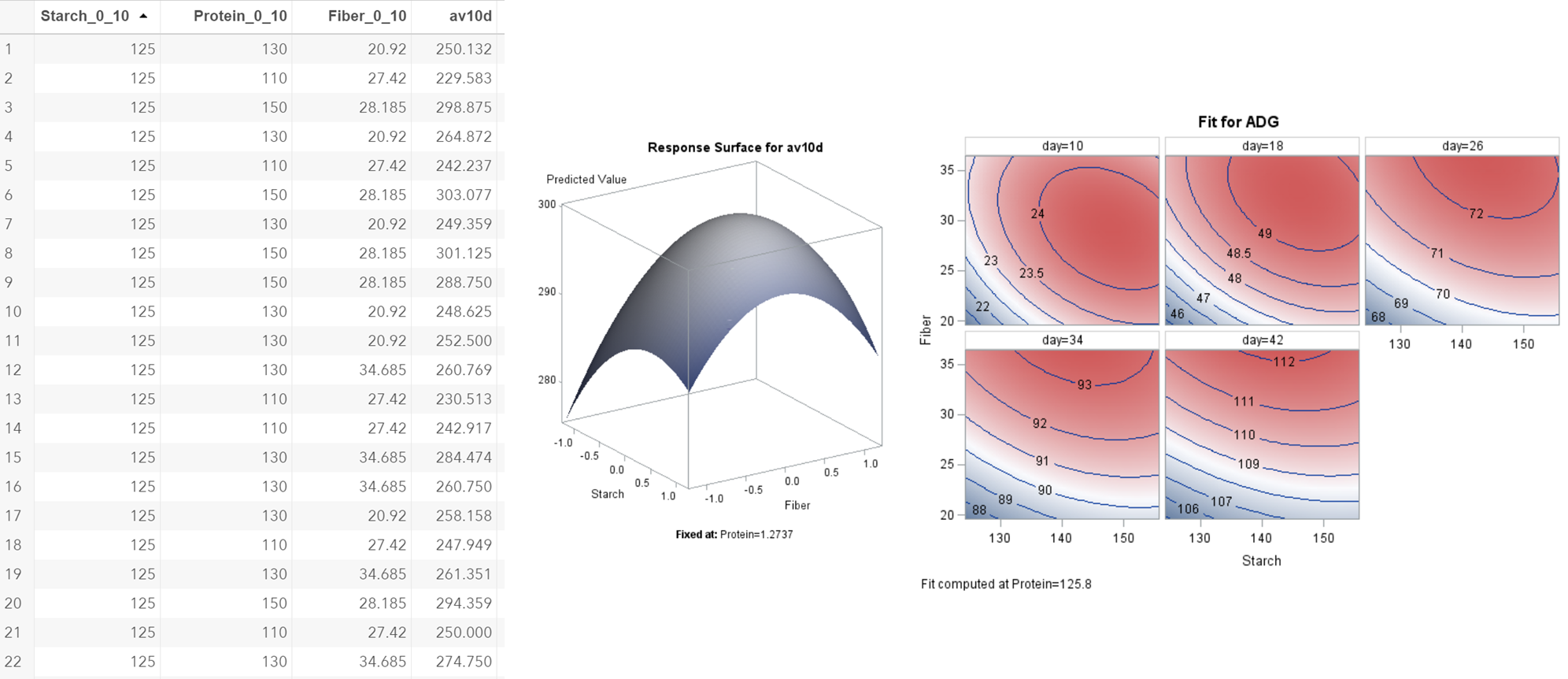
响应面示例,在 SAS 中进行分析。
每种剂量反应设计成功的关键是了解生物学。这听起来可能是一个悖论——如果您已经对剂量反应曲线有了很好的了解,为什么还要进行剂量反应设计呢?这是因为许多物质都遵循给定的化学式。因此,如果您已经了解了曲线,则可以最大化研究设计。这也带来了一个问题,因为方程的微小变化可能会导致剂量反应曲线的大幅波动。
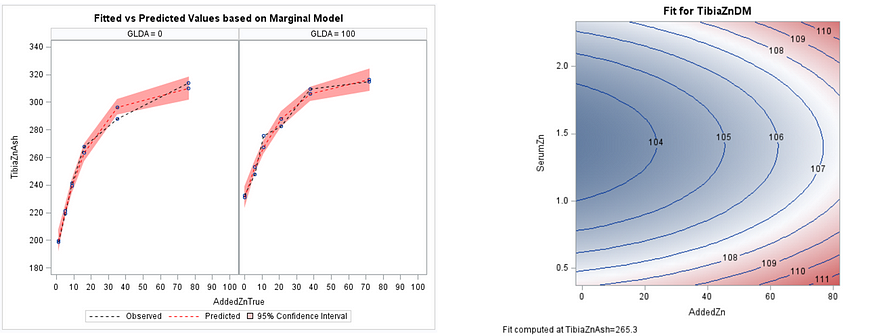
从 2D 到 3D。从剂量反应(左)到反应面(右)。响应面是一个山脊,这意味着我们无法看到整个关系,但它暗示着最小值。

有大量关于如何进行剂量反应研究的材料。
总之,如果您想找到最佳值,您需要以这样的方式设计和分析研究,以便您可以找到最佳值(如果它确实存在)。这意味着:
- 了解所包含变量的生物学。
- 了解他们是否以及如何相互作用。
- 创造一个可以实现最佳效果的机会之窗。
- 为一项研究提供动力,使机会之窗(如果它确实存在)变得可见。
三、样条曲线:别担心,我会保持简短
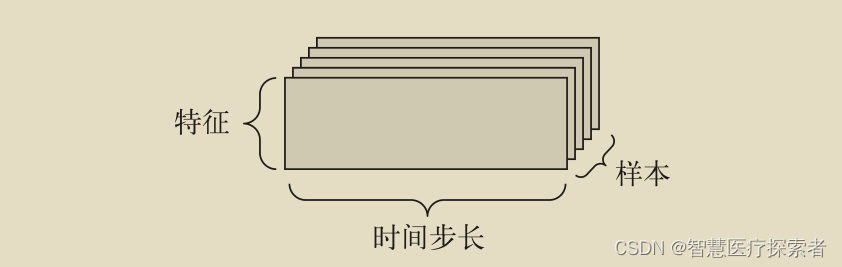
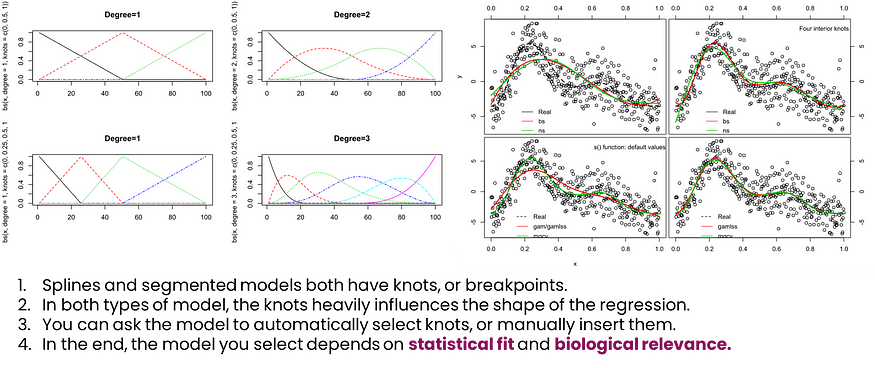
这不会是我关于样条线的第一段文字,也不会是我的最后一段,但我将主要使用图形来保持简短。下面,您可以看到样条线基本上是如何由连接件组成的。该图还将帮助您理解什么是折线回归。这是一条分段线性线。
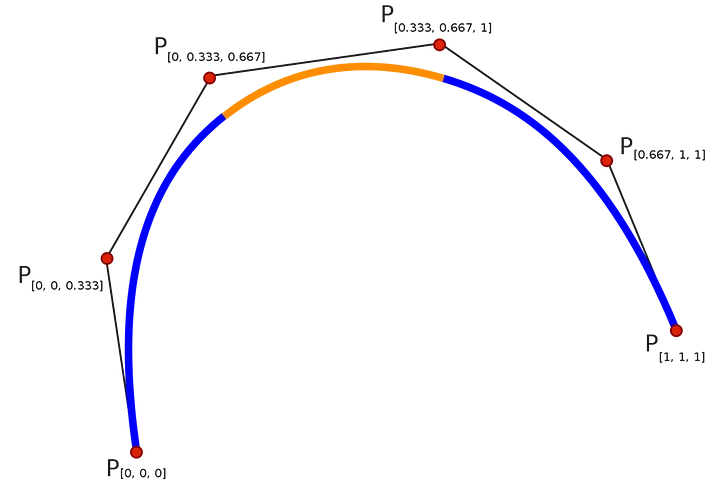

样条曲线已经超越了许多形式的旧回归方法,例如折线或多项式回归,可以找到最佳值。这就是为什么我们在解决折线回归之前显示样条线的原因。虽然样条建模有更多的建模自由度,但它也有更多的自由度来创建一些非常奇怪的关系。
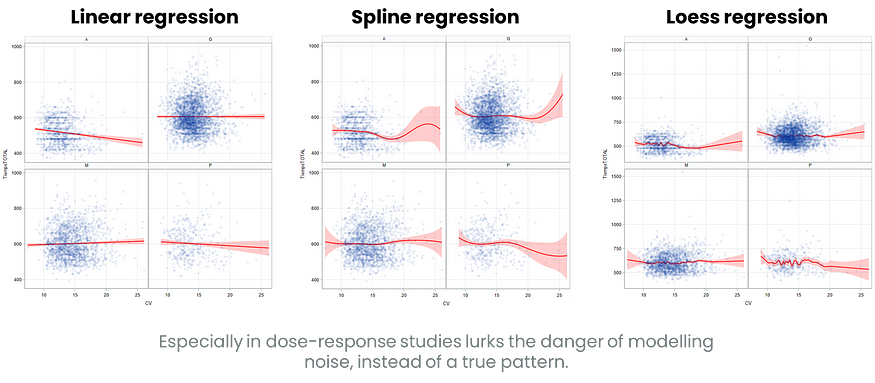
以上三种回归形式:线性、样条、LOESS。执行样条或 LOESS 回归很容易,但过度拟合的危险是真实存在的。
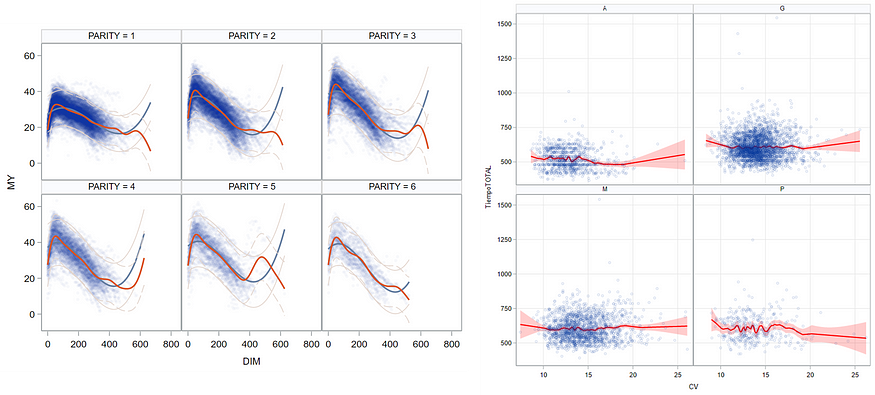
这里又举了两个例子,其中制作没有实际意义的曲线的危险是很容易完成的。请记住:我从一开始就说过,生物学、物理学、化学或任何潜在的因果机制都是至关重要的。并且优于无意识的统计拟合。
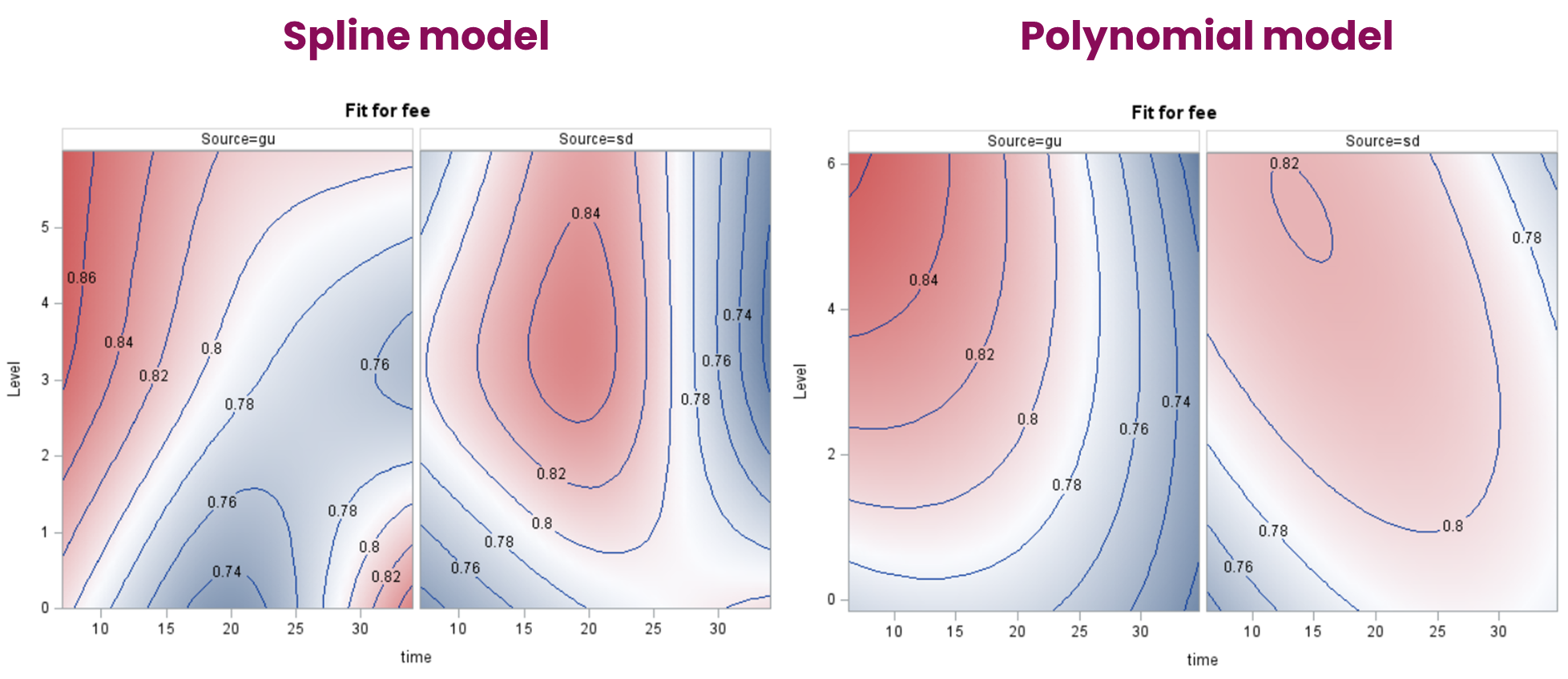
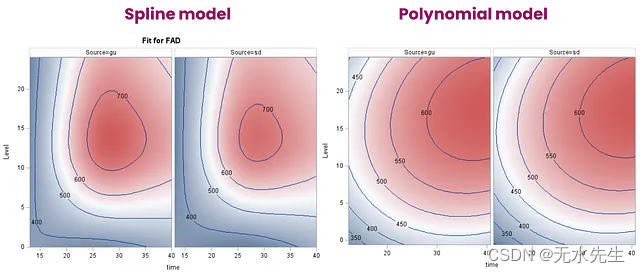
四、折线回归:以及为什么我们应该将其称为分段回归
折线回归有多个名称,其中包括:
1.分段回归
2.分段回归
3.断棍回归
4.曲棍球棒回归
也许,与其称之为折线,分段回归是一个更能说明问题的名称,因为它是该方法的核心。分段回归模型具有两个或多个子模型,每个子模型在解释变量的单独域上定义。最简单的分段回归模型假设:
- 当 X 小于某一阈值时,响应由一个参数模型建模。
- 当 X 大于阈值时,响应由一个参数模型建模。
阈值也称为断点、分割点、连接点或结点。
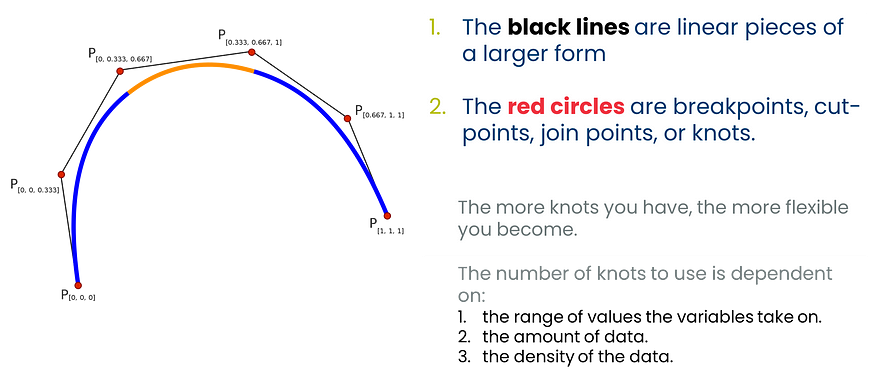
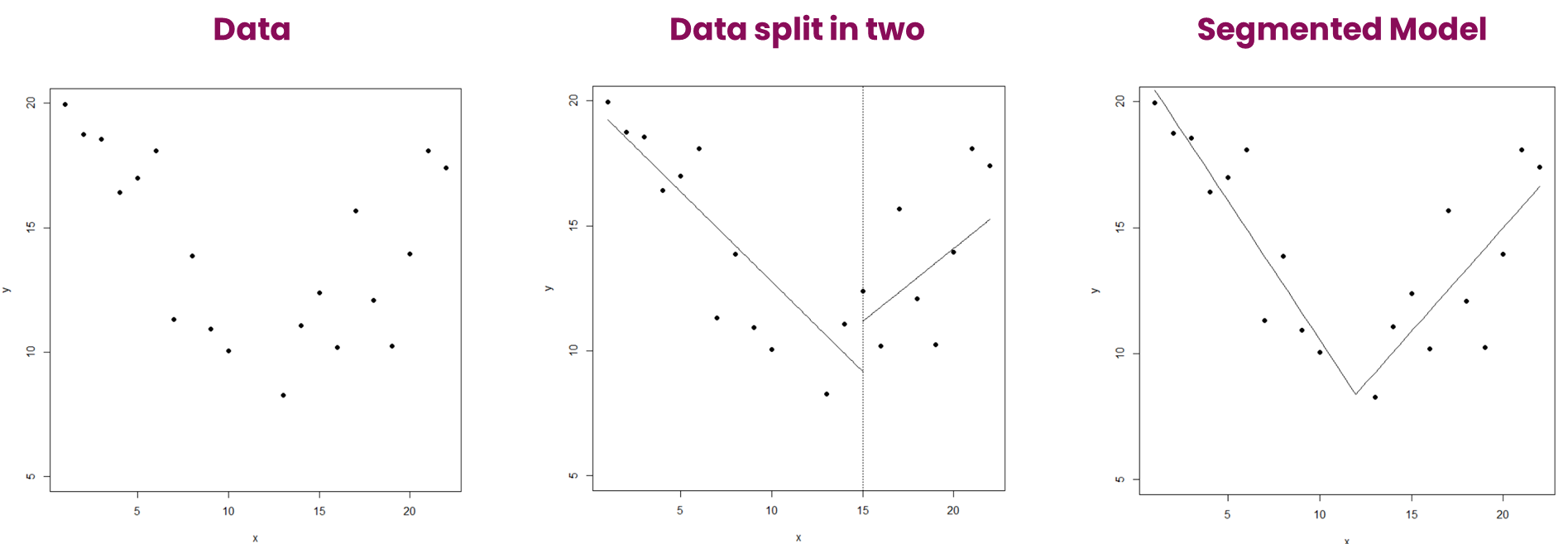
分段建模意味着分解数据。
但是,正如我之前所说,还有更高级的数据建模方法。尽管如此,这不应消除使用折线回归或分段回归(或分段回归——无论你怎么称呼它)的需要。

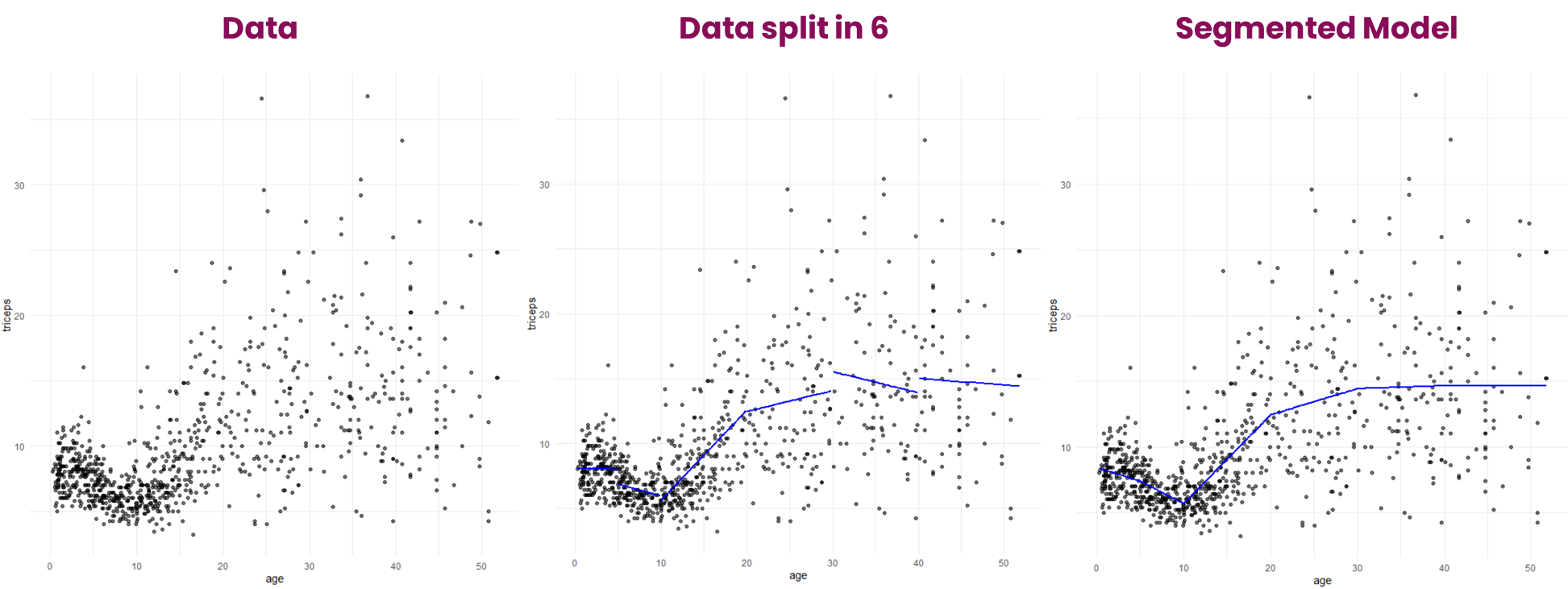
如今,建模变得相当容易。通过使用自动化,我们可以让算法找到最佳的切点。这种情况发生在各种回归中:多项式、分段、样条、LOESS、GAM 等。每次都会评估结果的可能性,直到找到最小值。
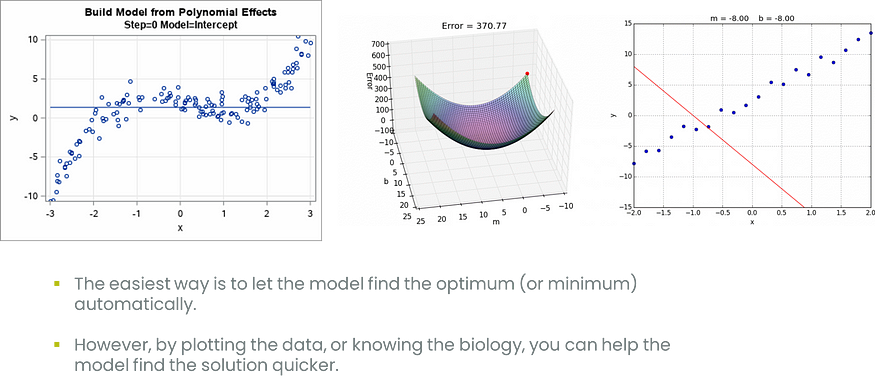
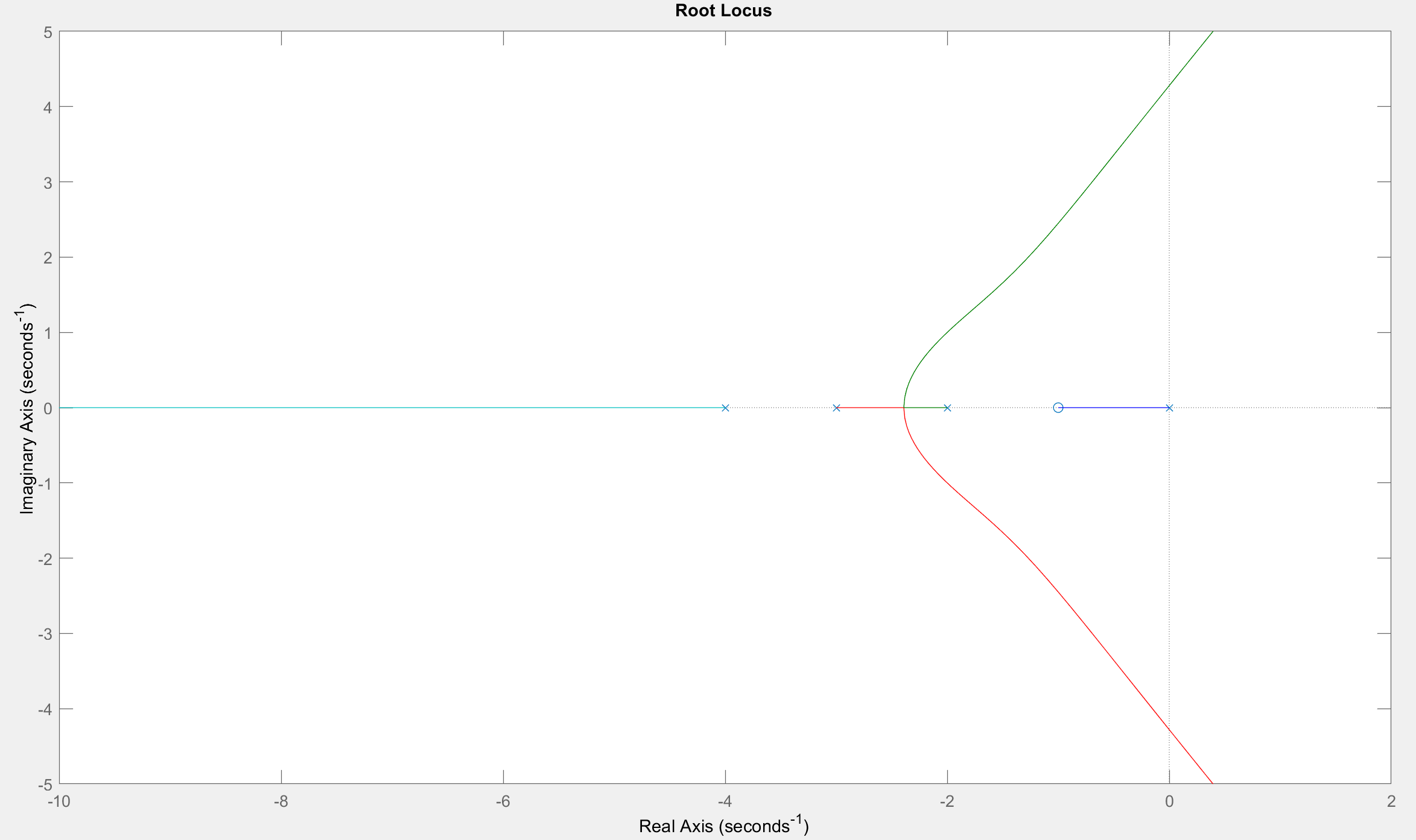
但是,我们也可以手动完成。它所需要的只是了解底层数据,并寻找断点有意义的点。最后,断点是回归线最好采取不同路线以维持最小 RMSE 的点。
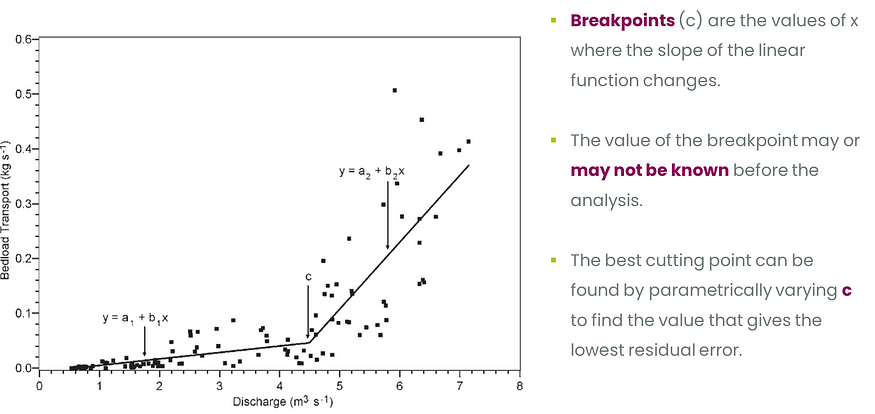
您可以在下面看到,无论是在理论上还是在 SAS 中,如何使用不同的函数来拟合非线性曲线。折线是有道理的,但很多时候并不是最佳解决方案。
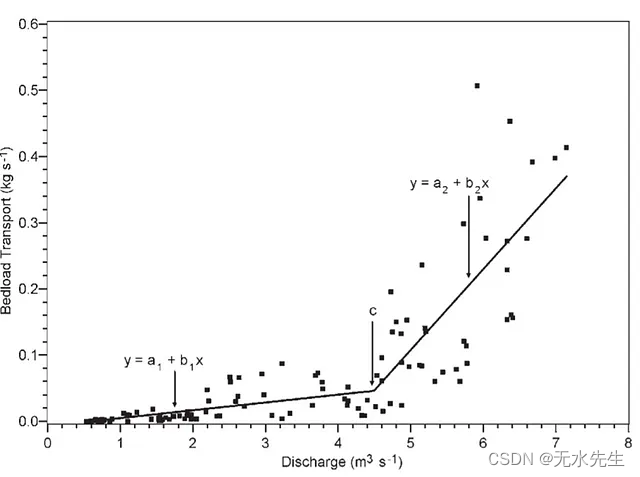

正如您所看到的,折线模型包含这样的假设:末端部件遵循一条不同的路径到达末端。这就是为什么单个断点很少是不够的,并且需要添加更多断点。添加足够的量,最终会得到一条样条线。

综上所述,折线回归应该称为分段回归。分段回归只不过是:
- 分解数据
- 分别分析一下
- 连接数据
- 迭代该过程
记住!折线通常不能提供模型的最佳拟合。
五、SAS 和 SAS 中的折线回归R:为什么软件并不重要
数据并不总是适合任何形式的分段建模。明智地选择了模特。
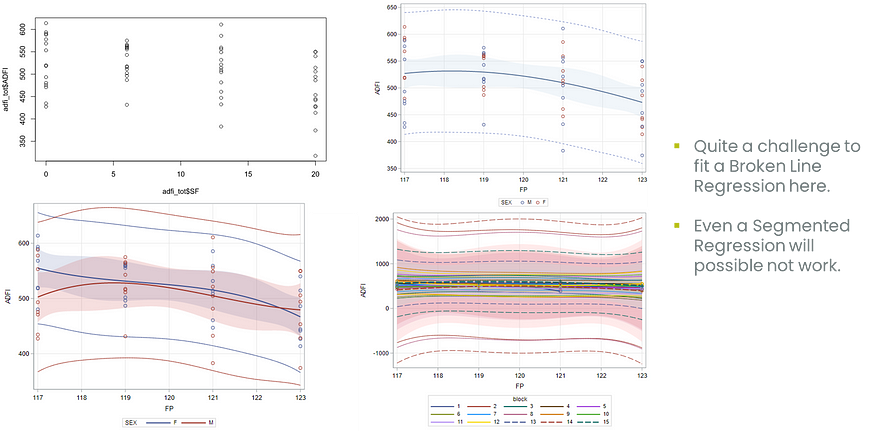
尝试在此类数据上拟合折线是没有意义的。
然而,这并不意味着不可能,正如您从下面的结果中看到的那样。不过,说实话,我宁愿符合大均值。
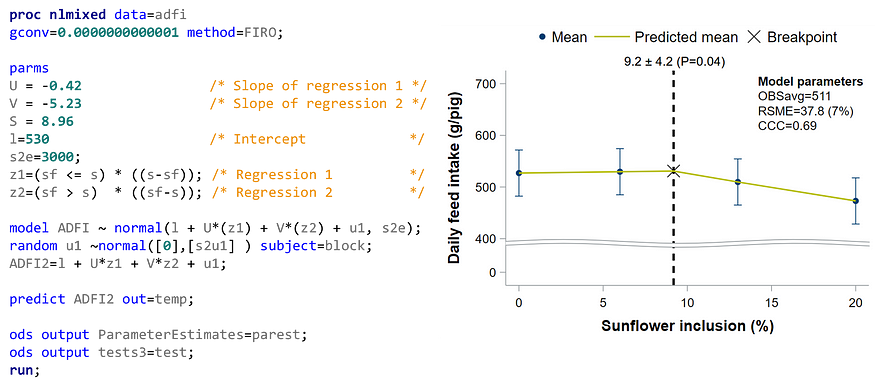
在SAS
我们也可以在 R 中使用用于分析分段模型的包来执行相同的操作。
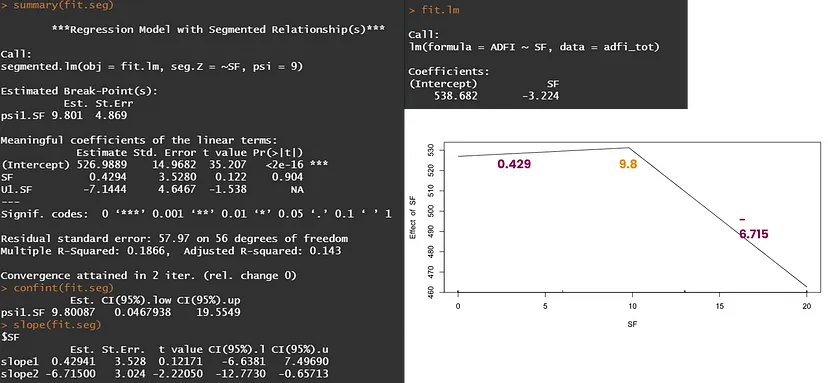
在 R 中,您可以看到断点 (9.8) 和系数。
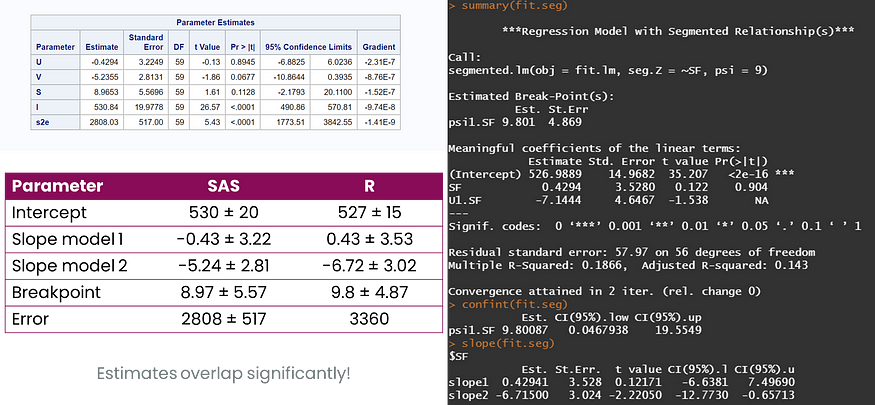
SAS 和 R 之间的结果比较。
正如您所看到的,数据来自随机块设计,因此我们可以添加随机组件 - 每个块 (ID) 一条折线。
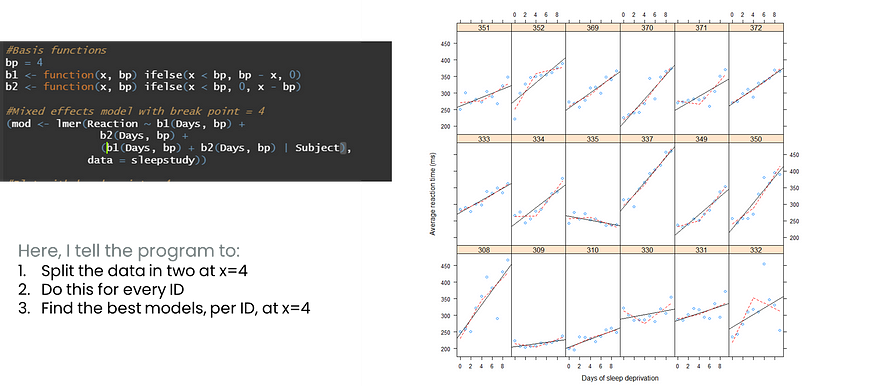
每个 ID 的分段回归
最后,我上面所做的大部分工作都是由 SAS 或 R 等程序自动完成的。请记住,简单的部分是建模,困难的部分是首先选择为什么要建模。如果一条断线真的有意义的话。
@marc.jacobs012