1 深度学习中的张量
在深度学习框架中,Tensor(张量)是一种数据结构,用于存储和操作多维数组。张量可以被视为一种扩展的矩阵,它可以具有任意数量的维度。
在深度学习中,张量通常被用来表示神经网络的输入、输出、权重和梯度等数据。在深度学习框架中,张量是一个重要的概念,因为它是深度学习计算的基本单位。
张量可以用不同的数据类型表示,如浮点型、整型等。在深度学习框架中,通常使用GPU来加速张量的计算,因为GPU具有并行计算能力,可以快速地执行大量的矩阵和向量运算。
深度学习框架通常提供了一些张量操作函数,如矩阵乘法、卷积、池化等,使得用户可以方便地进行张量计算。
2 张量的基本属性
主要有三个属性:秩、轴、形状
- 秩:主要告诉我们是张量的维度,其实就是告诉我们是几维向量,通过多少个索引就可以访问到元素。
- 轴:在张量中,轴是指张量的一个维度。当处理多维数据时,每个维度都可以被称为一个轴。通常,第一个轴称为0轴(或轴0),第二个轴称为1轴(或轴1),以此类推。
- 形状:形状是指张量在每个轴上的维度大小。它是一个由整数组成的元组,表示张量沿着每个轴的大小。
3 张量的维度
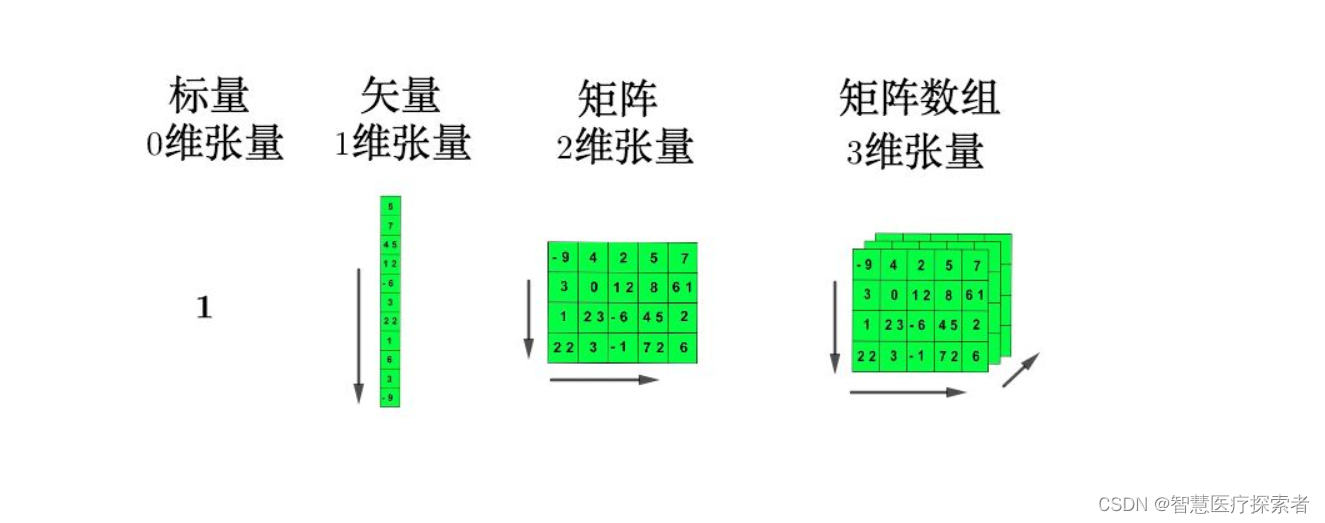
3.1 标量(0D 张量)
仅包含一个数字的张量叫作标量(scalar,也叫标量张量、零维张量、0D 张量)。在 Numpy中,一个 float32 或 float64 的数字就是一个标量张量(或标量数组)。你可以用 ndim 属性来查看一个 Numpy 张量的轴的个数。标量张量有 0 个轴( ndim == 0 )。张量轴的个数也叫作阶(rank)。下面是一个 Numpy 标量。
import numpy as np
x = np.array(12)
print(x.ndim)
x结果:
0
array(12)3.2 向量(1D 张量)
数字组成的数组叫作向量(vector)或一维张量(1D 张量)。一维张量只有一个轴。下面是一个 Numpy 向量。
import numpy as np
x = np.array([12, 3, 6, 14, 7])
print(x.ndim)
x结果:
1
array([12, 3, 6, 14, 7])注意:这个向量有 5 个元素,所以被称为 5D 向量。不要把 5D 向量和 5D 张量弄混! 5D 向量只有一个轴,沿着轴有 5 个维度,而 5D 张量有 5 个轴(沿着每个轴可能有任意个维度)。维度(dimensionality)可以表示沿着某个轴上的元素个数(比如 5D 向量),也可以表示张量中轴的个数(比如 5D 张量),这有时会令人感到混乱。对于后一种情况,技术上更准确的说法是 5 阶张量(张量的阶数即轴的个数),但 5D 张量这种模糊的写法更常见。
3.3 矩阵(2D 张量)
向量组成的数组叫作矩阵(matrix)或二维张量(2D 张量)。矩阵有 2 个轴(通常叫作行和列)。你可以将矩阵直观地理解为数字组成的矩形网格。下面是一个 Numpy 矩阵。
import numpy as np
x = np.array([[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]])
print(x.ndim)结果:
23.4 3D 张量与更高维张量
将多个矩阵组合成一个新的数组,可以得到一个 3D 张量,你可以将其直观地理解为数字组成的立方体。下面是一个 Numpy 的 3D 张量。
import numpy as np
x = np.array([[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]]])
print(x.ndim)结果:
3将多个 3D 张量组合成一个数组,可以创建一个 4D 张量,以此类推。深度学习处理的一般是 0D 到 4D 的张量,但处理视频数据时可能会遇到 5D 张量。
4 现实世界中的数据张量
我们现实中要处理的数据几乎总是以下类别之一:
-
向量数据:2D 张量,形状为 (samples, features) 。
-
时间序列数据或序列数据:3D 张量,形状为 (samples, timesteps, features) 。
-
图像:4D张量,形状为 (samples, height, width, channels) 或 (samples, channels,
-
height, width) 。
-
视频:5D张量,形状为 (samples, frames, height, width, channels) 或 (samples,frames, channels, height, width) 。
4.1 向量数据
这是最常见的数据。对于这种数据集,每个数据点都被编码为一个向量,因此一个数据批量就被编码为 2D 张量(即向量组成的数组),其中第一个轴是样本轴,第二个轴是特征轴。
两个例子:
- 人口统计数据集,其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值的向量,而整个数据集包含 100 000 个人,因此可以存储在形状为 (100000, 3) 的 2D张量中。
- 文本文档数据集,我们将每个文档表示为每个单词在其中出现的次数(字典中包含20 000 个常见单词)。每个文档可以被编码为包含 20 000 个值的向量(每个值对应于字典中每个单词的出现次数),整个数据集包含 500 个文档,因此可以存储在形状为(500, 20000) 的张量中。
4.2 时间序列数据或序列数据
当时间(或序列顺序)对于数据很重要时,应该将数据存储在带有时间轴的 3D 张量中。每个样本可以被编码为一个向量序列(即 2D 张量),因此一个数据批量就被编码为一个 3D 张量(见下图)
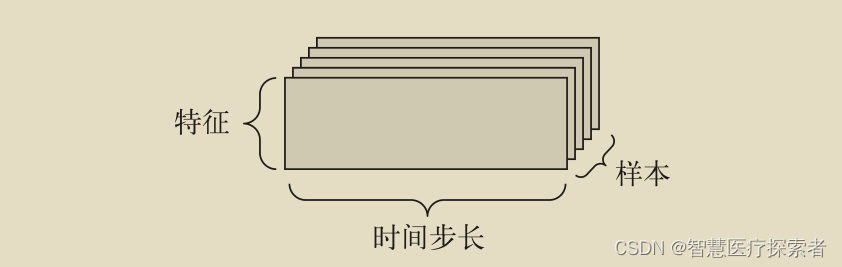
根据惯例,时间轴始终是第 2 个轴(索引为 1 的轴)。
两个例子:
- 股票价格数据集。每一分钟,我们将股票的当前价格、前一分钟的最高价格和前一分钟的最低价格保存下来。因此每分钟被编码为一个 3D 向量,整个交易日被编码为一个形状为 (390, 3) 的 2D 张量(一个交易日有 390 分钟),而 250 天的数据则可以保存在一个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
- 推文数据集。我们将每条推文编码为 280 个字符组成的序列,而每个字符又来自于 128个字符组成的字母表。在这种情况下,每个字符可以被编码为大小为 128 的二进制向量(只有在该字符对应的索引位置取值为 1,其他元素都为 0)。那么每条推文可以被编码为一个形状为 (280, 128) 的 2D 张量,而包含 100 万条推文的数据集则可以存储在一个形状为 (1000000, 280, 128) 的张量中。
4.3 图像数据
图像通常具有三个维度:高度、宽度和颜色深度。虽然灰度图像(比如 MNIST 数字图像)只有一个颜色通道,因此可以保存在 2D 张量中,但按照惯例,图像张量始终都是 3D 张量,灰度图像的彩色通道只有一维。因此,如果图像大小为 256×256,那么 128 张灰度图像组成的批量可以保存在一个形状为 (128, 256, 256, 1) 的张量中,而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中。
图像张量的形状有两种约定:通道在后(channels-last)的约定(在 TensorFlow 中使用)和通道在前(channels-first)的约定(在 Theano 中使用)。Google 的 TensorFlow 机器学习框架将颜色深度轴放在最后: (samples, height, width, color_depth) 。与此相反,Theano将图像深度轴放在批量轴之后: (samples, color_depth, height, width) 。如果采用 Theano 约定,前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256) 。Keras 框架同时支持这两种格式。
4.4 视频数据
视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧,每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_depth) 的 3D 张量中,因此一系列帧可以保存在一个形状为 (frames, height, width,color_depth) 的 4D 张量中,而不同视频组成的批量则可以保存在一个 5D 张量中,其形状为(samples, frames, height, width, color_depth) 。
举个例子:一个以每秒 4 帧采样的 60 秒 YouTube 视频片段,视频尺寸为 144×256,这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中。总共有 106 168 320 个值!如果张量的数据类型( dtype )是 float32 ,每个值都是32 位,那么这个张量共有 405MB。好大!你在现实生活中遇到的视频要小得多,因为它们不以float32 格式存储,而且通常被大大压缩,比如 MPEG 格式。