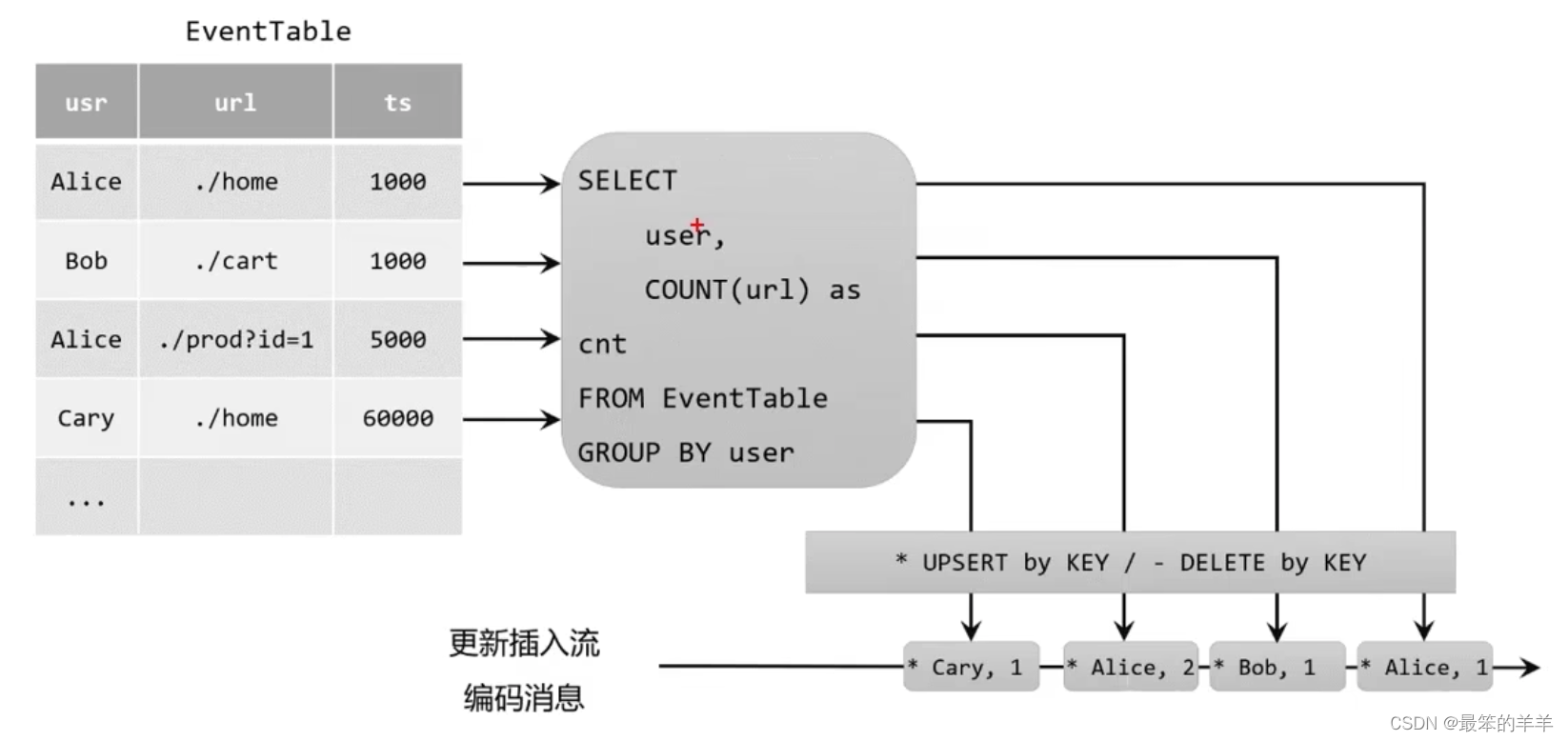
整数划分——完全背包的变形
- 一、题目
- 二、思路分析
- 1、状态转移方程
- (1)状态表示
- (2)方程书写
- 2、循环与初始化
- (1)循环
- (2)初始化
- 三、代码
一、题目

二、思路分析
这道题这么看的话还是比较抽象的,但是我们可以将其看作一个完全背包问题, n n n代表的是背包容量,后面的数字组成看作物品的体积,由于这些数字可以重复的使用,所以这道题类似于完全背包,但是在状态表示上还是有点区别的。
1、状态转移方程
(1)状态表示
f
(
i
,
j
)
f(i,j)
f(i,j):用体积范围[1,i]的物品,去恰好填满一个背包容量为j的书包,满足该要求的方案总数。
完全背包问题是在众多的方案中求一个最大值,而今天的这个问题是求一个总数。
(2)方程书写
这里就不过多的解释了,大家可以去看一看作者写的完全背包问题:
传送门:完全背包的详解与优化
f [ i ] [ j ] = s u m ( f [ i − 1 ] [ j − k i ] ) ( j ≥ k i ) f[i][j]=sum(f[i-1][j-ki])\ \ \ \ \ (j\geq ki) f[i][j]=sum(f[i−1][j−ki]) (j≥ki)
2、循环与初始化
(1)循环
循环设计的话,我们和背包问题保持一致。
for(int i=1;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
for(int k=0;k*i<=j;k++)
{
f[i][j]=(f[i][j]%mod+f[i-1][j-k*i]%mod)%mod;
}
}
}
(2)初始化
初始化的子问题是我们的最小子问题,找到最小子问题的方法就是将我们循环中的边界带进去。
比如这道题,我们的最小子问题就是当 i = 0 i=0 i=0或者 j = 0 j=0 j=0的时候,等式右边的值。
f [ 1 ] [ 0 ] = f [ 0 ] [ 0 ] + f [ 1 ] [ 0 ] f[1][0]=f[0][0]+f[1][0] f[1][0]=f[0][0]+f[1][0]
f [ 0 ] [ 0 ] f[0][0] f[0][0]和 f [ i ] [ 0 ] f[i][0] f[i][0]
就是我们要求的子问题, f [ 0 ] [ 0 ] f[0][0] f[0][0]表示用体积为0的物品装满容量为0的背包,很显然就1种方案。
而 f [ i ] [ 0 ] f[i][0] f[i][0]是指用体积范围1到i的东西装满背包容量为0的物品,很显然这是不合法的,初始化为0。
三、代码
#include<iostream>
using namespace std;
const int N=1e3+10,mod=1e9+7;
int f[N][N];
int n;
int main()
{
cin>>n;
f[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
for(int k=0;k*i<=j;k++)
{
f[i][j]=(f[i][j]%mod+f[i-1][j-k*i]%mod)%mod;
}
}
}
cout<<f[n][n]<<endl;
}
当然,我们可以使用优化后的方案:
#include<iostream>
using namespace std;
const int N=1e3+10,mod=1e9+7;
int f[N];
int n;
int main()
{
cin>>n;
f[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
f[j]=(f[j]%mod+f[j-i]%mod)%mod;
}
}
cout<<f[n]<<endl;
}
优化的思路在完全背包中有详细地讲解。